Contest #0 A题(暴力)
题目描述
小象同学在初等教育时期遇到了一个复杂的数学题,题目是这样的:
给定自然数
nn
n,确定关于
x,y,zx, y, z
x,y,z 的不定方程
x−n+y−z=0\displaystyle \sqrt{x - \sqrt{n}} + \sqrt{y} - \sqrt{z} =0的所有自然数解。
当时的小象同学并不会做这道题。多年后,经过高等教育的洗礼,小象同学发现这道题其实很简单。小象同学认为你一定也会做这道题,所以把这道题留给了你。为了便于输出,你不需要输出每一组解
(x,y,z)(x, y, z)
(x,y,z),你只需要给出解的数量和所有解的
xyzx y z
xyz 之和对
(109+7)(10^9+7)
(10
9
+7) 取模的值即可。注意,解的数量不对
(109+7)(10^9+7)(109+7) 取模。
输入描述
输入包含多组测试数据。输入的第一行包含一个正整数
TT
T (
1≤T≤1041 \leq T \leq10^4
1≤T≤10
4
),表示测试数据的组数。接下来依次描述每组测试数据,对于每组测试数据:
仅一行,包含一个非负整数
nn
n (
0≤n≤2×1090 \leq n \leq 2 \times 10^9
0≤n≤2×10
9
),含义如题面所示。
输出描述
对于每组数据,输出一行。若方程有无穷多组自然数解,则在这一行输出
“infty”\text{``infty''}
“infty”(不含引号),否则在这一行输出两个整数,其中第一个整数表示方程的解数,第二个整数表示所有解的
xyzx y z
xyz 之和对
(109+7)(10^9+7)
(10
9
+7) 取模的值,这两个整数之间用恰好一个空格隔开,行末不要有多余的空格。
样例输入 1
3
6
12
24
样例输出 1
0 0
1 12
2 72
提示
当
n=12n = 12
n=12 时,方程唯一的解为
x=4x = 4
x=4,
y=1y = 1
y=1,
z=3z = 3
z=3。
当
n=24n = 24
n=24 时,方程的两组解为
x=5x = 5
x=5,
y=2y = 2
y=2,
z=3z = 3
z=3 和
x=7x = 7
x=7,
y=1y = 1
y=1,
z=6z = 6
z=6。
将题目公式化简,得到 x=z+y;n=4zy;

两种情况需要特判:
1.是n可以开方的时候,x2=n,z=y,z和y可以取任意的自然数,属于方程有无穷多组自然数解的情况.
2.因为z和y是自然数,如果有解,n=4zy,那么n肯定是可以被4整除的;不能被4整除时,输出0 0;
分割线:--------------------------------------------------------------------------------------------------------------------------
吐槽:这道题居然卡long long,n用ll会TLE,这我还是第一次遇到.有听人说过ll运算慢,但是以前还没遇到,这次总算见识到了.呜呜呜呜,我好菜啊.
只会写a题,让各位见笑了.
#include <bits/stdc++.h>
using namespace std;
const int N=1e9+7;
int main()
{
int t;
scanf("%d",&t);
while(t--){
int n;
int ans=0;
int cnt=0;
scanf("%d",&n);
int p=sqrt(n);
if(p*p==n){
puts("infty");continue;
}
if(n%4!=0){
puts("0 0");continue;
}
n/=4;
for(int y=1;ll(y*y)<=n;y++){
if(n%y==0){
cnt++,ans=(ans+((n/y+y)*ll(n))%N)%N;
}
}
printf("%d %d\n",cnt,ans);
}
return 0;
}

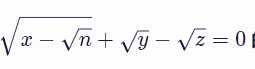

 浙公网安备 33010602011771号
浙公网安备 33010602011771号