Wunder Fund Round 2016 (Div. 1 + Div. 2 combined) D. Hamiltonian Spanning Tree

time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
A group of n cities is connected by a network of roads. There is an undirected road between every pair of cities, so there are roads in total. It takes exactly y seconds to traverse any single road.
A spanning tree is a set of roads containing exactly n - 1 roads such that it's possible to travel between any two cities using only these roads.
Some spanning tree of the initial network was chosen. For every road in this tree the time one needs to traverse this road was changed from y to x seconds. Note that it's not guaranteed that x is smaller than y.
You would like to travel through all the cities using the shortest path possible. Given n, x, y and a description of the spanning tree that was chosen, find the cost of the shortest path that starts in any city, ends in any city and visits all cities exactly once.
Input
The first line of the input contains three integers n, x and y (2 ≤ n ≤ 200 000, 1 ≤ x, y ≤ 109).
Each of the next n - 1 lines contains a description of a road in the spanning tree. The i-th of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n) — indices of the cities connected by the i-th road. It is guaranteed that these roads form a spanning tree.
Output
Print a single integer — the minimum number of seconds one needs to spend in order to visit all the cities exactly once.
Examples
Input
Copy
5 2 3
1 2
1 3
3 4
5 3
Output
Copy
9
Input
Copy
5 3 2
1 2
1 3
3 4
5 3
Output
Copy
8
Note
In the first sample, roads of the spanning tree have cost 2, while other roads have cost 3. One example of an optimal path is .

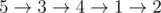
In the second sample, we have the same spanning tree, but roads in the spanning tree cost 3, while other roads cost 2. One example of an optimal path is .

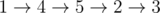
题解:给了一个无向完全图,还有一个生成树,在生成树上的边的权值为x,不在生成树上的权值为y,让你求一条最短路径(闭环的),经过所有的点,有且仅有一次经过.

根据x,y的大小先分类讨论:

1.x>y时,,尽量走不在树上的边.在普通情况下,总能找到不在上的边,所以cost就为y*(n-1).

特殊情况,如:菊花图

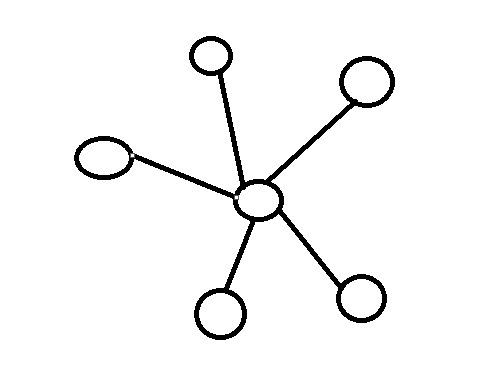
po主亲自绘制.

这个特判即可,详见代码.

2.x<y时,尽量走在树上的边,dfs跑一下,记录一下树上可用的边,找出最长的那一条,剩下的用y来连接,cos为cntx+(n-1-cnt)y.

#include <bits/stdc++.h>
const int N=2e5+5;
typedef long long ll;
using namespace std;
vector<int> v[N];
int du[N];
ll cnt=0;
bool dfs(int n,int m){
    int left=2;
    for(unsigned i=0;i<v[n].size();i++){
        int w=v[n][i];
        if(w==m) continue;
        bool flag=dfs(w,n);
        if(flag&&left>0){
            cnt++;
            left--;
        }
    }
    return left>0;
}
int main()
{
    ll n,x,y;
    scanf("%I64d%I64d%I64d",&n,&x,&y);
    for(int i=1;i<n;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        du[a]++;
        du[b]++;
        v[a].push_back(b);
        v[b].push_back(a);
    }
    ll ans=0;
    if(x<=y){
        dfs(1,-1);
        ans=cnt*x+(n-1-cnt)*y;
    }
    else{
        int flag=0;
        for(int i=1;i<=n;i++){
            if(du[i]==n-1) flag=1;
        }
        if(flag) ans=(n-2)*y+x; else ans=(n-1)*y;

    }
    printf("%I64d\n",ans);
    //cout << "Hello world!" << endl;
    return 0;
}