线性逻辑回归与非线性逻辑回归pytorch+sklearn
1 import matplotlib.pyplot as plt 2 import numpy as np 3 from sklearn.metrics import classification_report 4 from sklearn import preprocessing 5 6 # 载入数据 7 data = np.genfromtxt("LR-testSet.csv", delimiter=",") 8 x_data = data[:, :-1] 9 y_data = data[:, -1] 10 11 12 def plot(): 13 x0 = [] 14 x1 = [] 15 y0 = [] 16 y1 = [] 17 # 切分不同类别的数据 18 for i in range(len(x_data)): 19 if y_data[i] == 0: 20 x0.append(x_data[i, 0]) 21 y0.append(x_data[i, 1]) 22 else: 23 x1.append(x_data[i, 0]) 24 y1.append(x_data[i, 1]) 25 26 # 画图 27 scatter0 = plt.scatter(x0, y0, c='b', marker='o') 28 scatter1 = plt.scatter(x1, y1, c='r', marker='x') 29 # 画图例 30 plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best') 31 32 33 plot() 34 plt.show() 35 36 # 数据处理,添加偏置项 37 x_data = data[:,:-1] 38 y_data = data[:,-1,np.newaxis] 39 40 print(np.mat(x_data).shape) 41 print(np.mat(y_data).shape) 42 # 给样本添加偏置项 43 X_data = np.concatenate((np.ones((100,1)),x_data),axis=1) 44 print(X_data.shape) 45 46 47 def sigmoid(x): 48 return 1.0 / (1 + np.exp(-x)) 49 50 51 def cost(xMat, yMat, ws): 52 left = np.multiply(yMat, np.log(sigmoid(xMat * ws))) 53 right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat * ws))) 54 return np.sum(left + right) / -(len(xMat)) 55 56 57 def gradAscent(xArr, yArr): 58 xMat = np.mat(xArr) 59 yMat = np.mat(yArr) 60 61 lr = 0.001 62 epochs = 10000 63 costList = [] 64 # 计算数据行列数 65 # 行代表数据个数,列代表权值个数 66 m, n = np.shape(xMat) 67 # 初始化权值 68 ws = np.mat(np.ones((n, 1))) 69 70 for i in range(epochs + 1): 71 # xMat和weights矩阵相乘 72 h = sigmoid(xMat * ws) 73 # 计算误差 74 ws_grad = xMat.T * (h - yMat) / m 75 ws = ws - lr * ws_grad 76 77 if i % 50 == 0: 78 costList.append(cost(xMat, yMat, ws)) 79 return ws, costList 80 # 训练模型,得到权值和cost值的变化 81 ws,costList = gradAscent(X_data, y_data) 82 print(ws) 83 84 plot() 85 x_test = [[-4], [3]] 86 y_test = (-ws[0] - x_test * ws[1]) / ws[2] 87 plt.plot(x_test, y_test, 'k') 88 plt.show() 89 90 # 画图 loss值的变化 91 x = np.linspace(0,10000,201) 92 plt.plot(x, costList, c='r') 93 plt.title('Train') 94 plt.xlabel('Epochs') 95 plt.ylabel('Cost') 96 plt.show()


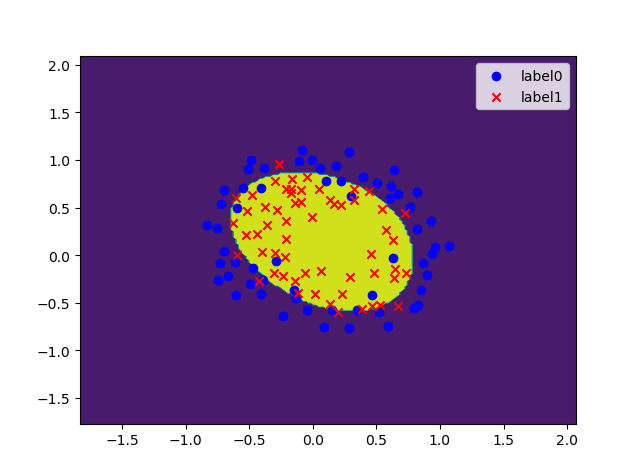
1 import matplotlib.pyplot as plt 2 import numpy as np 3 from sklearn.metrics import classification_report 4 from sklearn import preprocessing 5 from sklearn.preprocessing import PolynomialFeatures 6 7 # 载入数据 8 data = np.genfromtxt("LR-testSet2.txt", delimiter=",") 9 x_data = data[:, :-1] 10 y_data = data[:, -1, np.newaxis] 11 12 13 def plot(): 14 x0 = [] 15 x1 = [] 16 y0 = [] 17 y1 = [] 18 # 切分不同类别的数据 19 for i in range(len(x_data)): 20 if y_data[i] == 0: 21 x0.append(x_data[i, 0]) 22 y0.append(x_data[i, 1]) 23 else: 24 x1.append(x_data[i, 0]) 25 y1.append(x_data[i, 1]) 26 27 # 画图 28 scatter0 = plt.scatter(x0, y0, c='b', marker='o') 29 scatter1 = plt.scatter(x1, y1, c='r', marker='x') 30 # 画图例 31 plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best') 32 33 34 plot() 35 plt.show() 36 37 # 定义多项式回归,degree的值可以调节多项式的特征 38 poly_reg = PolynomialFeatures(degree=3) 39 # 特征处理 40 x_poly = poly_reg.fit_transform(x_data) 41 42 43 def sigmoid(x): 44 return 1.0 / (1 + np.exp(-x)) 45 46 47 def cost(xMat, yMat, ws): 48 left = np.multiply(yMat, np.log(sigmoid(xMat * ws))) 49 right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat * ws))) 50 return np.sum(left + right) / -(len(xMat)) 51 52 53 def gradAscent(xArr, yArr): 54 xMat = np.mat(xArr) 55 yMat = np.mat(yArr) 56 57 lr = 0.03 58 epochs = 50000 59 costList = [] 60 # 计算数据列数,有几列就有几个权值 61 m, n = np.shape(xMat) 62 # 初始化权值 63 ws = np.mat(np.ones((n, 1))) 64 65 for i in range(epochs + 1): 66 # xMat和weights矩阵相乘 67 h = sigmoid(xMat * ws) 68 # 计算误差 69 ws_grad = xMat.T * (h - yMat) / m 70 ws = ws - lr * ws_grad 71 72 if i % 50 == 0: 73 costList.append(cost(xMat, yMat, ws)) 74 return ws, costList 75 76 # 训练模型,得到权值和cost值的变化 77 ws,costList = gradAscent(x_poly, y_data) 78 print(ws) 79 80 # 获取数据值所在的范围 81 x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1 82 y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1 83 84 # 生成网格矩阵 85 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), 86 np.arange(y_min, y_max, 0.02)) 87 88 z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据 89 for i in range(len(z)): 90 if z[i] > 0.5: 91 z[i] = 1 92 else: 93 z[i] = 0 94 z = z.reshape(xx.shape) 95 96 # 等高线图 97 cs = plt.contourf(xx, yy, z) 98 plot() 99 plt.show()

导入数据:1. LR-testSet.csv
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.53862 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
0.667394 12.741452 0
-2.46015 6.866805 1
0.569411 9.548755 0
-0.026632 10.427743 0
0.850433 6.920334 1
1.347183 13.1755 0
1.176813 3.16702 1
-1.781871 9.097953 0
-0.566606 5.749003 1
0.931635 1.589505 1
-0.024205 6.151823 1
-0.036453 2.690988 1
-0.196949 0.444165 1
1.014459 5.754399 1
1.985298 3.230619 1
-1.693453 -0.55754 1
-0.576525 11.778922 0
-0.346811 -1.67873 1
-2.124484 2.672471 1
1.217916 9.597015 0
-0.733928 9.098687 0
-3.642001 -1.618087 1
0.315985 3.523953 1
1.416614 9.619232 0
-0.386323 3.989286 1
0.556921 8.294984 1
1.224863 11.58736 0
-1.347803 -2.406051 1
1.196604 4.951851 1
0.275221 9.543647 0
0.470575 9.332488 0
-1.889567 9.542662 0
-1.527893 12.150579 0
-1.185247 11.309318 0
-0.445678 3.297303 1
1.042222 6.105155 1
-0.618787 10.320986 0
1.152083 0.548467 1
0.828534 2.676045 1
-1.237728 10.549033 0
-0.683565 -2.166125 1
0.229456 5.921938 1
-0.959885 11.555336 0
0.492911 10.993324 0
0.184992 8.721488 0
-0.355715 10.325976 0
-0.397822 8.058397 0
0.824839 13.730343 0
1.507278 5.027866 1
0.099671 6.835839 1
-0.344008 10.717485 0
1.785928 7.718645 1
-0.918801 11.560217 0
-0.364009 4.7473 1
-0.841722 4.119083 1
0.490426 1.960539 1
-0.007194 9.075792 0
0.356107 12.447863 0
0.342578 12.281162 0
-0.810823 -1.466018 1
2.530777 6.476801 1
1.296683 11.607559 0
0.475487 12.040035 0
-0.783277 11.009725 0
0.074798 11.02365 0
-1.337472 0.468339 1
-0.102781 13.763651 0
-0.147324 2.874846 1
0.518389 9.887035 0
1.015399 7.571882 0
-1.658086 -0.027255 1
1.319944 2.171228 1
2.056216 5.019981 1
-0.851633 4.375691 1
-1.510047 6.061992 0
-1.076637 -3.181888 1
1.821096 10.28399 0
3.01015 8.401766 1
-1.099458 1.688274 1
-0.834872 -1.733869 1
-0.846637 3.849075 1
1.400102 12.628781 0
1.752842 5.468166 1
0.078557 0.059736 1
0.089392 -0.7153 1
1.825662 12.693808 0
0.197445 9.744638 0
0.126117 0.922311 1
-0.679797 1.22053 1
0.677983 2.556666 1
0.761349 10.693862 0
-2.168791 0.143632 1
1.38861 9.341997 0
0.317029 14.739025 0
2.LR-testSet2.txt
0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0



