信号完整性（SI）电源完整性（PI）学习笔记（二）时域与频域

时域与频域
1.时域：是真实的世界，是唯一存在的域。
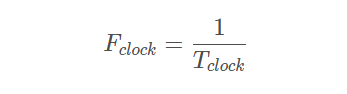其中：
Fclock​是时钟频率，单位为GHz.
Tclock​是时钟周期，单位为ns.
根据逻辑系列可知，下降时间通常比上升时间短一些（由典型CMOS输出驱动器的设计造成的）

上升边：信号从低电平跳变到高电平所经历的时间（10%~90%或20%-80%）20%-80%作为品质因数会好一些，IBIS模型常常用。一般而言，驱动器下降沿比上升沿更短，因为N管比P管导通速度快。

2.频域：频域是数学构造的，正弦波是频域中唯一存在的波形，这是频域中最重要的法则。
在频域中解决问题：①频域中不能产生新的信息；②阻抗在时域和频域中都有定义，在频域中分析阻抗问题是首选；③在频域中考虑电源和地分布阻抗，可以对轨道塌陷问题提供更好的解决方法。

3.正弦波的特性：可知正弦波是频域中唯一存在的波形，时域中用3项可以定义一个正弦波，而在频域中只表示一个点。频率f，幅度A，相位可以描述正弦波的角频率w=2πf;理想正弦波直流值或平均值始终为0；相位：在时间轴起点的波的起始位置，对于若干个频率点，幅值的集合称为频谱。计算时域波形频谱的唯一方法就是—傅里叶变换。

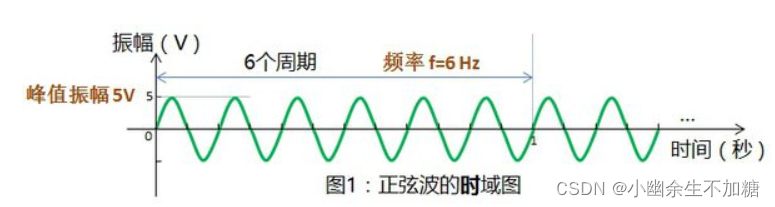
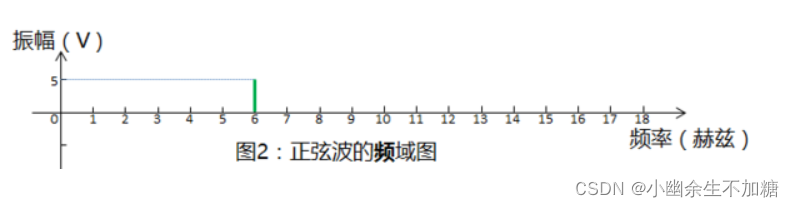
4.傅里叶变换：波形从时域变到频域频谱
工业中常常会同时使用到 FI , DFT 和 FFT 这二种方法。现在我们知道这三种算法之间是有区别的，但同时它们又有着同样的用途——将时域波形变换成频域频谱。

傅里叶积分（FI）

傅里叶积分(FI) 是一种将时域的理想数学表示变换成频域描述的数学技术。例如，若时域中的整个波形只是一个短脉冲，就可以用傅里叶积分将它变换到频域中去。傅里叶积分是在整个时间轴上从负无穷大到正无穷大做积分，得到的结果是零频率到正无穷大频率上连续的频域函数。在这个区间上，每个连续的频率值都对应一个幅值。

离散傅里叶变换（DFT)

使用离散傅里叶变换(DFT) 可以将这个波形变换到频域中。其中基本的假设就是原始的时域波形是周期的，每隔T 秒重复一次。不像积分，此处仅使用到求和，通过简单的数学方法就可以将任意一组数据变换到频域中。

快速傅里叶变换（FFT）

除了计算每一个频率点的幅度值的实际算法使用了快速矩阵代数学的技巧之外，它与离散傅里叶变换是完全一样的。这种快值算法只应用于时域中的数据点个数是2 的幕数的情况，如256 点， 512 点或1024 点。根据所计算电压点个数的多少，快速傅里叶变换的计算速度比普通的离散傅里叶变换可以快100 到10000 倍。

离散傅里叶变换的条件是该波形是重复的，是周期的。
频谱中的正弦波频率应该是重复频率的整数倍；第一个正弦波频率称之为1次谐波，第二个正弦波频率称为2次谐波。。。。。。所有谐波及其幅度称为频谱。

5.理想方波的频谱
（1）所有偶次谐波（如2GHz，4GHz,6GHz）的幅度都为0，只有奇次谐波具有非零值，这是任何波形都具有的特征，其波形的后半部分恰好是前半部分求反的结果。我们将这些波形称为反对称波形或奇对称波形。
（2）奇次谐波的幅度：

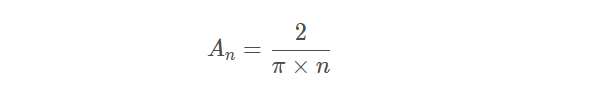An​ ：n次谐波的幅度
n ：谐波数，为奇数

频率分量提高时，其幅度随着1/f 的减小而减小。
如果理想方波的电压跳变范围增加为原来的两倍，即从0V 到 2V, 那么各次谐波的幅度也加倍。

特殊的频率值： 0Hz。因为正弦波的均值为0, 任何正弦波的组合也只能描述时域中均值为0 的波形。如果给出一个直流偏移，即非零均值，那么直流分量就存储在零频率值中。这有时也称为零次谐波，其幅度与信号的均值相等。在方波占空比为50% 的情况下，零次谐波幅度为0.5V。

①正弦波频率分量及其幅度的集合称为频谱，每一分旦称为谐波；
② 零次谐波就是直流分量值；
③对于理想方波占空比为50% 这一特殊情况，偶次谐波的幅度为0;
④任何谐波的幅度都可由2/ (nπ）计算得出。

6.从频域变换到时域
频域中的频谱表示的是时域波形包含的所有正弦波频率的幅度。如果我们知道频谱，要想观察它的时域波形，只需将每个频率分量变换成它的时域正弦波，再将其全部叠加即可。这个过程称为傅里叶逆变换。

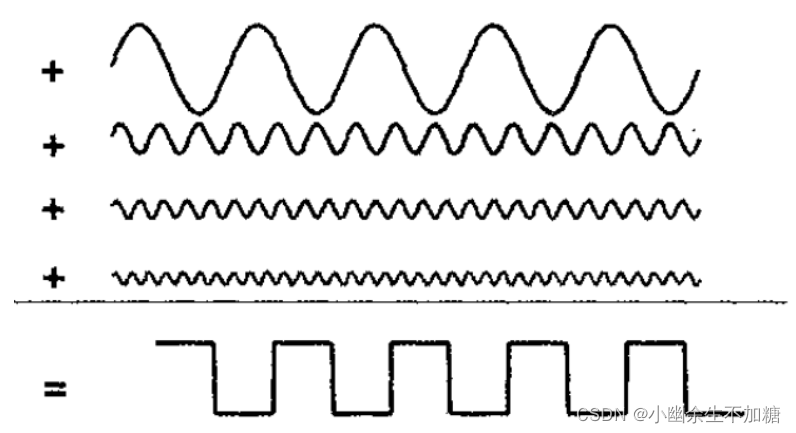
频域中的每个分量都是时域中定义在 t = − ∞ t=-∞ t=−∞ 到 + ∞ +∞ +∞ 上的正弦波。为了重新生成时域波形，可以提取出频谱中描述的所有正弦波，并在时域中的每个时间间隔点处把它们叠加。从低频端开始，把频谱中的各次谐波叠加，就可得到时域中的波形。

7.带宽对上升边的影响
（1）带宽用于表示频谱中最高的有效正弦波频率分量值；
（2）在设计射频产品的互联线时，重要的是要求其阻抗在一个相对较窄的带宽内受控；在高速数字产品中的互联线，重要的是要求其阻抗在一个很宽的带宽内受控，这点往往很难。
（3）波形的带宽值越大，10%~90%上升边就越短，上升边越短，与理想方波的波形就越接近。同理，若降低信号的带宽（比如删除高频分量）则上升边会变长。

8.上升边与带宽

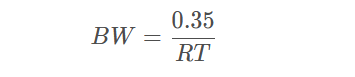
其中：
BW 表示带宽，单位为 GHz
RT 表示10%~90%上升时间，单位为 ns
例如，若信号的上升时间为1ns，则带宽约为350MHz。

对于其他波形，如高斯或指数边沿的波形，也可以用另外一些方法得到这样的关系式。对于方波，采用的纯粹是实验途径，没有做任何假设。用这一经验公式所表示的是一个非常有用的经验法则。

9.“有效”的含义
将信号的带宽定义为有效的最高正弦波频率分量。

（1）理想方波的频谱中的频率分量可延伸到尤穷大，要想得到零上升时间的理想方波，每个分债都是必需的，而且是有效的。

（2）对于实际的时域波形，随着频率的升高，其谱分量的幅度总是比理想方波中相同频率的幅度下降得快。有效性问题其实就是一个频率点的问题，高于该点的谐波分量的幅度比理想方波中相应频率分量的幅度要小。

（3）所谓“小”，通常指的是该分最的功率要小于理想方波中相应频率分量幅度功率的50%,功率下降50% 也就是幅度下降至70%, 这才是有效性的真正定义。若幅度高于理想方波中相同谐波幅度的70% 以上，则称之为有效。

    对于上升时间有限的任何波形，有效指的是信号的谐波幅度高于相同频率的理想方波中相应谐波幅度的70% 时的那一点

从另一个稍微不同的角度看， 可以把有效定义为实际波形的谐波分量开始比 1 / f 1/f 1/f下降得快时的那个频率点，该颇率有时也称为拐点频率，理想方波的谐波幅度的下降速率近似于 1 / f 1/f 1/f . 所以实际波形的谐波幅度开始明显偏离理想方波时的频率，就是拐点频率，

要估算时域波形的带宽、我们实际上是在问： 刚刚超过理想方波中相应谐波幅度70% 的最高频率分量是什么？当实际波形的谐波幅度已明显低于理想方波中相应谐波的幅度时， 那些幅度更低的谐波对减少1上升时间已没有明显作用，于是这些分量就可以忽略了。

使用DFT计算波形的频谱并与理想方波相比较，可以得到任何波形的带宽，从而可以确定出波形中小于理想方波的70% 的那个频率分量，或者使用前面导出的经验公式，即BW 是由0.35/ (上升时间）得出的。

10.实际信号的带宽
（1）除了基于上升边去近似波形的带宽，其他计算基本上不能用手工完成；
（2）接近于理想方波质量信号都有一个简单地特征，即如果传输线路的端接欠佳，则信号会发生振铃，频谱在振铃频率下出现峰值，会比没有振铃时的信号幅度高10倍以上
（3）将带宽保持在最低值，辐射量就会保持在最小值。

11.时钟频率与带宽
对于两个不同的波形，可以有相同的时钟频率，值上升时间和带宽却很可能不同。仅知道时钟频率并不能告诉我们带宽

上升时间与时钟周期有什么关系： 原则上讲，两者之间的唯一约束是：上升时间一定小于周期的50% 。除此之外没有任何限制，上升时间可以是周期的任意百分比，当时钟频率达到器件工艺的极限，如1GHz 时，上升时间可能是周期的25% 。在许多微处理器产品中，典型的上升时间可能是周期的10%, 在高端ASIC 驱动外部低时钟频率存储器总线时，上升时间还可能是周期的5% 。当板级总线属千老式系统时，上升时间甚至可能只有周期的1% 。

经验假设： 上升时间是周期的7%（有挑战，但是是接近的），大部分接近10%这样，上升时间就被低估了，带宽则被高估了，而这比带宽被低估要安全得多。

最终关系表达式： 带宽是时钟频率的五倍
BWclock = 5 × Fclock

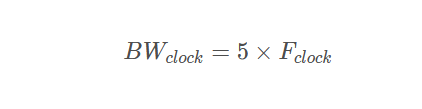
BWclock​表示时钟带宽的近似值，单位为GHz,
Fclock​, 表示时钟频率，单位为GHz,

如果时钟频率是100MHz, 则信号的带宽就是500MHz, 。如果时钟频率是1 GHz, 那么信号带宽就是5GHz, 。

这就是说，时钟波形中的最高正弦波频率分量通常就是第五次谐波。

12.测量的带宽
测量的带宽是指有足够精度时的最高正弦波频率分量。也就是测量仪器在测量不同的参数时，在保证精度满足的情况下能够达到的最高测量频率。
对于时域工作的测量仪器，TDR，他的测量带宽取决于他能输出到被测元器件的信号的最快上升边。

13.模型的带宽
模型的带宽是指，当我们采用理想的电气模型来进行等价时，这种理想的电气模型成立是在一定的频率区间内的。能够使这个模型基本满足实际情况的最大正弦波频率就是该模型的带宽。

14.互联的带宽
互连线的带宽是指能被互连线传输且损耗不是很大的最高正弦波频率分量。这里的损耗不一定是指其幅度的损耗，在远距离电视电缆系统中，接收端甚至可以使用只有源端功率的1%的信号。实际上，互连线的带宽是指互连线能够传输的满足实际应用性能指标的最高正弦波分量。

互连线的带宽是对互连线所能传轮的住号最短上升时间的直接度量

互连线的3dB 带宽指的是信号衰减小于一3dB 时的正弦波频率。

一般来说，如果某频率的幅值在传输前后该频率的幅值减少小于3dB，也就是说幅值减少为入射值的70%以上，那么这种频率的信号我们认为是有效的。也就是说，如果我们说一个互连线的带宽是8GHz，那么我们对这个互连线输入一个8GHz的正弦波，远端得到的信号幅度最多为原信号幅度的70%。如果我们对这个互连线输入的正弦波的频率小于8GHz，那么远端得到的信号的幅度会大于原信号幅度的70%以上。也就是说，经过互连线传播后，低于8GHz的谐波被传输，高于8GHz的谐波分量变得不再是有效成分了。

此外，由于传输线对于信号是有损传播，仅此传输前的信号的上升时间经过传输后会增加，因此这里有个经验法则，就是，如果想要比较好的传播1GHz的信号，互连线的带宽至少为该信号带宽的两倍，即2GHz。