信号完整性（SI）电源完整性（PI）学习笔记（三）阻抗与电气模型
阻抗与电气模型
1.用阻抗描述信号完整性
（1）信号是指变化的电压或变化的电流 。所有信号完整性问题都是由模拟信号（变化的电压或者电流）与互联电气特性之间的相互作用引起的，而影响信号的关键电气特性是互联的阻抗。
（2）阻抗被定义为电压和电流之比：
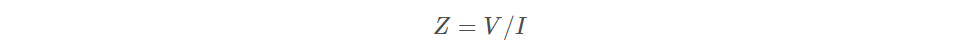知道了互联的阻抗和传播时延，也就知道了它的几乎所有的电气特性。
（3）以下问题都可以用阻抗加以描述
①任何阻抗突变都会引起电压信号的反射和失真，这使信号质量会出现问题。如果信号所感受到的阻抗保持不变，就不会发生反射，信号也不会失真。衰减效应是由串联和并联阻抗引起的。
②信号的串扰是由两条相邻信号线条（当然还有它们的返回路径）之间的电场和磁场的耦合引起的，信号线间的互耦合电容和互耦合电感产生的阻抗决定了耦合电流的值。
③电源供电轨道的塌陷实际上与电源分布系统(PDS) 的阻抗有关。系统中必然流动着一定的电流量以供给所有的芯片，并且由于在电源和地之间存在着阻抗，所以当芯片电流切换时，就会形成压降。这个压降意味着电源轨道和地轨道从正常值向下塌陷。
④最大的EMI 根源是流经外部电缆的共模电流，此电流由地平面上的电压引起。在地平面上返回路径的阻抗越大，电压降即地弹就越大，由它再激起辐射电流。减少电缆电磁T 扰的最常用力法是在电缆周围使用铁氧体扼流圈，这主要是为了增加共模电流所受到的阻抗，从而减少共模电流。
⑤阻抗是解决信号完整性问题方法学的核心。
（4）建模和仿真这两个关键步骤是：把物理特性转化成阻抗描述，分析阻抗对信号的影响。
2.阻抗的含义
（1）阻抗的定义适用于所有场合，无论在时域还是在频域中，也不管是测量实际元件还是计算理想元件。
（2）电阻是电阻器这类理想电路元件固有的品质因数，阻抗又称之为交流（AC）电阻。
（3）开路元件阻抗无穷大，短路元件阻抗Z=0。
3.实际电路元件与理想电路元件
实际的： 是可测的，是实际存在的事物，它们是构成现实的硬件系统的互连线或元件， 实际的器件包括板上的线条，封装中的引线或装在板上的去耦电容等。
理想的： 是特殊的电路元件的数学描述，有详细而精确的定义。仿真器只能仿真理想器件的性能，电路理论的概念和形式仅适用于理想器件，而且模型也是由理想器件组合而成的。
（1）通常仿真器只能仿真由理想电路元件描述的电路
（2）四种理想的两端电路元件：
①理想电阻器
②理想电容器
③理想电感器
④理想传输线
（3）对于实际电路元件，除非先测得其S参数行为模型，否则无法计算其阻抗。
（4）我们的最终目的是建立由理想电路元件组成的等效电路模型，模型的阻抗和测量实际元件得出的阻抗非常接近。
（5）只能测量实际元件，也只能计算和仿真理想元件。
4.时域中理想电阻器的阻抗
理想电阻两端的电压与流过的电流之间的关系如下：
V = I × R V=I×R V=I×R
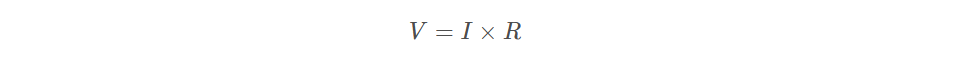
式中：
V 表示电阻两端的电压
I 表示流过电阻的电流
R 表示电阻值
在时域中，运用阻抗的定义和理想元件的定义，可以计算出一个理想电阻的阻抗：
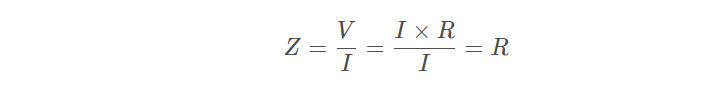
Z = V/ I = I × R /I = R
Z=R
这就是说，理想电阻的阻抗是恒定的，且与电压和电流无关。电阻的阻抗确实很简单。
5.时域中理想电容器的阻抗
（1）理想电容器的容值：
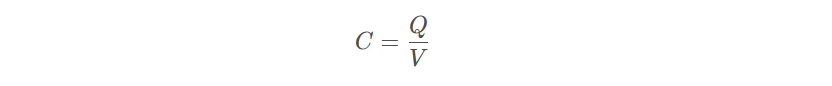式中：
C 表示电容，单位为 F (法拉）
V 表示两极板之间的电压差，单位为 V (伏特）
Q 表示在极板之间存储的电荷，单位为 C (库仑）
电容器的电容值描述了它在一定电压下存储电荷的能力。
（2）电容器的阻抗只能由两端的电压和流过的电流求得，
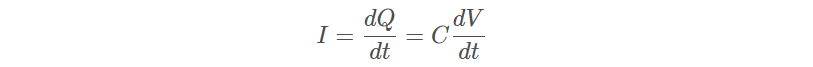式中：
I 表示流过电容器的电值
Q 表示电容器一个极板上的电荷量
C 表示电容器的电容值
V 表示电容器两端的电压
如果电容器两端的电压变化很快，则流过的电流就会很大。如果电压几乎不变的话，流过的电流也就接近于零。利用这个关系，可以在时域中计算出理想电容器的阻抗：
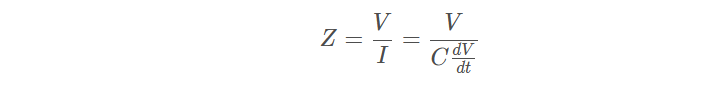式中：
V 表示电容器两端的电压
C 表示电容器的电容值
I 表示流过电容器的电流
它表明电容器的阻抗与它两端的电压波形的确切形状有关。如果电压波形的斜率很大（也就是说电压变化很快），则流过的电流就很大，而且电容器的阻抗会很小。同样也表明在电压信号的变化率相同时，电容器的电容值越大，它的阻抗就越小。
- 时域中理想电感器的阻抗、
（1）理想电感器：
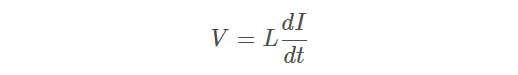式中：
V 表示电感两端的电压
L 表示电感器的电感值
I 表示值过电感器的电流
上式表明电感器两端的电压与流过电流的变化快慢有关。如果电流是个常数，那么电感器两端的电压就是零。同理，如果流过的电流迅速地变化，那么电感器两端的压降就很大。电感值是一个比例常数，它反应了电流变化时，所产生电压的敏感程度。所以大电感意味着变化小的电流也可以产生一个大电压。
（2）电感器的阻抗即电感器两端的电压与流经电感器的电流之比：
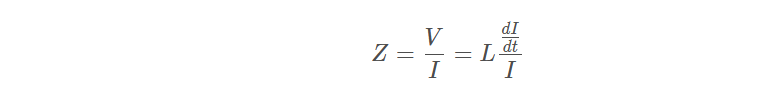
式中：
V 表示电感器两端的电压
L 表示电感器的电感
I 表示流过电感器的电流
**电感阻抗的一般特点：**如果流过电感器的电流迅速地增加，那么阻抗就很大，也就是当电流突然变化时，阻抗是非常大的；如果流过的电流只有很微弱的变化，则电感器的阻抗就非常小。对于直流电流来说，电感器的阻抗近似为零。
7.频域中的阻抗
（1）在频域中仅需处理正弦电压和正弦电流，运用这个新观点，可以从另一种角度来分析阻抗。正弦波有且仅有三个特征：每个波形相应的频率、幅度、相位。
（2）相位一般用弧度来描述，一个圆周是2π弧度，所以1rad约57°，以弧度每秒为单位的频率称为角频率：w，w=2πf
（3）计算两个正弦波的比值时，需要计算两个波形的幅度之比和两者之间的相移。
（4）两个正弦波的比值不是正弦波，而是一些包含了每个频率点上的幅度比值和相移信息的数据。这个比值的幅值只是两正弦波幅度之比：
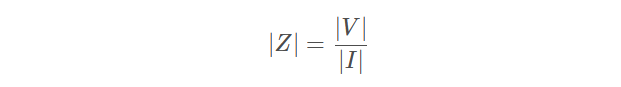电压幅度和电流幅度之比称为阻抗的幅值，其单位是欧姆。阻抗的相位就是两波形之间的相移，单位是度或是弧度。
（5）在频域中，电路元件或电路元件组合的阻抗可以表示成：20MHz 频率时，阻抗的幅值是 15 Ω, 相位是 25度。也就是说，阻抗是 15Ω , 电压比电流超前 25度。
（6）我们可以推出重要结论：任何电路元件的阻抗由两个数组成：在每个频率点上的幅值和相位。在描述阻抗时，需要指出它在哪个频率下的阻抗。
（7）频域中电阻器的阻抗：
如果施加正弦电流使之流过电阻，则在电阻两端就会得到一个正弦电压，它是R 和正弦电流的乘积：
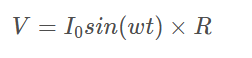
若采用电压与电流的比值表示电阻的阻抗，会发现阻抗就是电阻值：
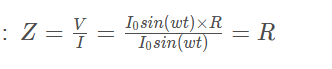
我们可以得出：**电阻阻抗与频率无关，且相移为零。**在任何频率上，理想电阻的阻抗都是相等的。这和我们在时域中看到的结果完全一致。
（8）频域中电容器的阻抗
频率越高，流经电容器的电流幅度就越大，这表明电容器的阻抗会随着频率的增大而减小。电容器的阻抗可由下式计算得到：
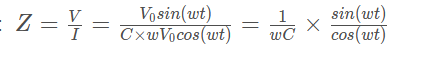
电容器阻抗的幅值就是 1/wC，当角频率增加时，电容的阻抗减小。阻抗的相位就是正弦波和余弦波之间的相移，即-90 度。
（9）频域中电感器的阻抗
加正弦电流流经电感，则产生的电压是：
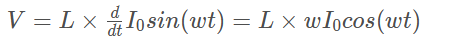
上式表明，当电流的幅度固定不变时，频率越高，电感两端的电压就越大。也就是说，频率升高时，需要更高的电压，才能使相同幅度的电流流经电感。电感器的阻抗随着频率的升高而增大。
运用阻抗的基本定义，可以推导出电感的阻抗在频域中的表示：
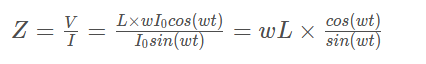
电感的阻抗的幅值为 wL。频率越高，交流电流要流经电感器就越困难，这是电感特性所产生的结果。电感器的阻抗的相位就是电压和电流之间的相移，即+90 度。
电感在实际高频中起主导作用。
（10）理想电容器的容值和理想电感器的感值是绝对不会随频率变化的常数，它们的阻抗会随着频率的变化而变化。
8.等效电路模型
（1）等效电路模型有两个特征：
①给出电路元件怎样连接在一起（称为拓扑结构）
②确定每个电路元件的值（称为参数值和寄生值）
（2）确定互联参数值的国产称为寄生参数提取。
（3）对于每个模型，经常会提出两个问题：优质度和带宽。
带宽是指按模型预估阻抗与真正实测阻抗非常吻合时的最高正弦波频率。
（4）通常把建立最简单的模型称为一阶模型，后续复杂度增加的模型与实际元件更加吻合，我们把后续的模型称为二阶、三阶模型。
（5）很明显，实际原件的复杂性能可以用理想电路元件的组合在很高的带宽以内，准确的加以逼近。
9.电路理论和SPICE
（1）电路理论是用一套严格定义又相对直接的公式描述理想电路元件组成的阻抗，一个比较重要的规则就是两个或多个元件串联时的组合阻抗等于各个元件的阻抗之和。
例如：近似于实际电容的RLC电路模型的阻抗为：
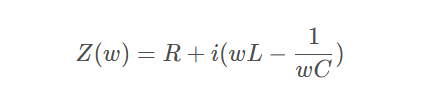
（2）有源器件包括信号源（电流和电压波形），实际晶体管模型或门模型。无源器件主要指R,L,C,T。
非线性器件指一些半导体元件，二极管，晶体管及模型。
（3）无论是在时域还是频域中仿真，SPICE仿真器都能预估出电路中任意一点的电压和电流，其中时域仿真称为瞬态仿真，频域仿真称为交流仿真。
（4）如果能够画出电路原理图，SPICE软件就可以仿真电压和电路波形，在SPICE中，用于交流仿真的电路器件之一是恒流正弦波电压源。
