信号完整性（SI）电源完整性（PI）学习笔记（四）电阻的物理基础

1.所有互连线的电气特性都完全可以应用麦克斯韦方程来描述、这四个方程描述了电场和磁场是如何与边界条件（即一些几何结构中的导体和介质）相互作用的。
所有互联和无源元件的电气描述都基于3种理想的集总电路元件（电阻器、电容器和电感器）和一个分布元件（传输线）。

2.优化系统物理设计的关键是：能够根据物理设计准确地预估出系统的电气性能，并且根据要求的电气性能又能更高效地优化物理设计。

3.考察互联电气性能最简单的出发点就是他的等效电路模型，所有模型都由两部分组成：电路拓扑结构和各个电路元件的参数值。

4.建立了互联电路模型的拓扑结构后，下一步就是提取参数值，这个过程有时称为寄生参数提取或寄生提取。

5.互联电阻：

什么是将物理设计转化为电气性能： 建模就是将物理设计中线的长、宽、厚和材料特性转化为 R , L 和 C的电气描述形式。

对于导线横截面恒定的这种特殊情况，电阻值可以由下式近似得出：

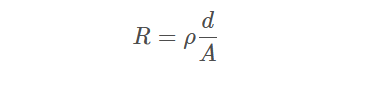
其中：
R 表示电阻值，单位为 Q ， ρ 表示导线的体电阻率，单位为 Ω ⋅ c m
d 表示互连线两端的距离，单位为 c m
A 表示横截面积，单位为 cm^2

6.经验法则： 直径为1mil 、长为80mil的键合线的电阻值大概是0.1Ω。(材质：金)
7.通常用希腊字母 ρ表示材料的体电阻率，另一个术语“电导率”描述材料的导电能力，通常用σ表示：

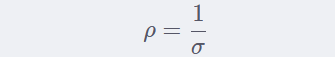
电阻率的单位是 Ω⋅m, 而电导率的单位是1/(Ω•m)。定义 1/Ω的单位为 S(西门子），所以电导率的单位是 S/m 。

要注意由于工艺条件的不同，大多数互连线材料的体电阻率的变化范围高达10% 。

​
8.单位长度电阻：
若导线的横截面是均匀的，则互连线电阻与长度成正比。对于均匀横截面的导线，其单位长度的电阻是恒定的：

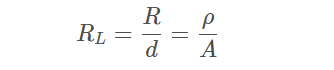
其中：
RL​表示单位长度电阻
d 表示互连线长度
ρ 表示体电阻率
A 表示电流流过的横截面积

9.经验法则： 键合线的单位长度电阻大约是 1 Ω / i n。常见的键合线长度是 0.1in, 所以典型的阻值大约是 1 Ω /i n × 0.1 i n = 0.1Ω 。

10.方块电阻：
许多互连线衬底，例如印刷电路板、防火陶瓷基片和薄胶膜基片，都制备有几个均匀的导体平面层，格据版图模板再布成不同的线条。每一层上所有的导线都有相同的厚度。

对于这种线条宽度相同的特殊情况，线条的电阻如下：

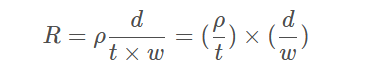
第一项， (ρ/t) ，对于该层上厚度为 t 的所有线条来说，是个常数。在同一层上的所有线条都有相同的体电阻率和相同的厚度，所以这一项称为“层方块电阻值”，并用 Rsq​表示。

第二项， (d/w)，是长与宽的比值。这是线条上能够划分的方块数目，用 n 来表示，且是个无量纲的数。所以矩形线条的电阻可以写为： R = R s q × n。

其中：
Rsq​表示方块电阻
n表示方块的数目
单位为 Ω

理解方块电阻的最简单方法就是认为它是正方形导体片断（也就是长等于宽）两端间的电阻。在这种情况下， n=1, 正方形线条两端间的电阻就是方块电阻。不管正方形的边长是10 mil 还是10 in, 其相对两端间的电阻是恒定不变的。如果长度加倍，可以以为阻值会加倍，然而宽度也加倍了，所以又使阻值减半。这两种作用相互抵消，因此当正方形的尺寸改变时，净电阻会保持不变。
经验法则：0.5 盎司铜的方块电阻是 1 m Ω / s q。5 mil 宽、5 in 长的线条可以截取成1000 个串联的方块并且阻值是1Ω。

11.方块电阻测量

只要这些探针远离边缘（即到任何一边至少为4 倍探针间距），测量的电阻与实际的探针间距就完全无关。

四脚探针： 这四个触点通常安装到刚性支架上，这样就可以使它们处在同一条直线上并且有相同的间距。将这四个探针与被测的
导体层接触放置，并连接到四点电阻分析仪或欧姆表。这样，当在最外边的两个触点施加恒定的电流时，内侧的两个触点间的电压就可以测量出来了。

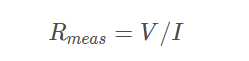
方块电阻 Rsq可以由测量的电阻计算：

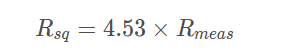
如果知道导体层的方块电阻，就可以计算出单位长度电阻和该导体层中所有导线的电阻。线条通常用宽度w 和长度d 来定义，所以线条的单位长度电阻用下式计算：

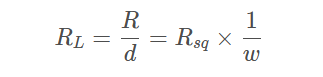
其中：
RL​ 表示单位长度电阻
R 表示线条电阻
Rsq​ 表示方块电阻
w 表示线条宽度
d 表示线条长度

12.由于趋肤效应的影响，线条的阻值将随着频率的升高而加丸虽然铜的体电阻率不变但导线上的电流分布却发生了变化。高频信号分量在贴近表面的很薄的层上传播，这使得有效横截面积减小了。对于1 盎司的铜导线，电阻在20MHz 处开始增加。导线的电阻在高频时会增加。

13.“不要对预测结果无知的情况下进行仿真或测量！！！”