信号完整性（SI）电源完整性（PI）学习笔记（七）电感的物理基础（二）

电感的物理基础 二

为了清楚起见，对于自感或互感，需要指明其电流源头。然后还要说明所指的是部分电路的局部电感，还是整个电路的回路电感。如果考虑的是某一段电路上的电压噪声，则由于该电压噪声取决于所有的磁力线匝数及其变化，所以需要并清楚在该段电路上的总电感。最后，如果是多个电感形成的组合（如封装中多条引线并联或多个过孔并联时），就要用到等效电感。

分类如下：

电感： 流过单位安培电流时，环绕在导体周围的磁力线匝数。
自感： 导体中流过单位安培电流时，环绕在该导体周围的磁力线匝数。
互感： 某一导体流过单位安培电流时，环绕在另一导体周围的磁力线匝数。
回路电感： 流过单位安培电流时，环绕在整个电流回路周围的磁力线总匝数。
回路自感： 完整电流回路流过单位安培电流时，环绕在该回路周围的磁力线总匝数。
回路互感： 某一完整电流回路流过单位安培电流时，环绕在另一回路周围的磁力线总匝数。
局部电感： 其他地方没有其他电流存在时，环绕在该段导线周困的磁力线忡数。
局部自感： 仅在一段导线中有单位安培电流而在其他地方无其他电流存在时，环绕在该段导线自身周围的磁力线匝数。
局部互感： 仅在某一段导线中有单位安培电流，而其他地方无其他电流存在时，环绕在另一段导线周围的磁力线匝数。
有效电感、净电感或总电感： 当整个回路流过单位安培电流时，环绕在一段导线周围的磁力线总匝数，其中包括源自回路每一部分电流的磁力线。
等效电感： 多个电感的串联或并联相对应的单个自感的大小，其中包括互感的影响。

1.回路中某一段的有限电感，净电感或总电感是指回路中的电流为单位安培时，环绕在该段周围的磁力线匝数总数。包括整个回路中任何电流段的磁力线匝数。

2.最小化返回路径上的电压降（地弹电压）只有两种方法：
（1）减小回路电流变化率
（2）尽可能减小Ltotal
Ltotal=​(Lb​+Lab​)减小支路的局部自感，增大两支路之间的局部互感。

3.在电源分配网络系统中，减小任意一条支路净电感的常用设计是：尽可能让同向平行电流之间的间距大于他们的长度。

4.在同一焊盘中有多个过孔的另一个重要的优点是由于与电源、地平面的接触面积加大，进入电源，地面的扩散电感将会减小。

5.电流方向相同的过孔之间的中心距应大于过孔长度，电流方向相反的孔之间的中心距应小于过孔的长度。

6.在实际中， 电流总是作完整的回路中流动。我们把该完整电流回路的总电感称为回路电感。回路电感事实上就是整个电流向路的自感，或者回路自感。

电流回路的回路自感就是当回路中流过单位安培电流时，环绕在整个回路周围的磁力线总匝轧数也让是回路中电流为 1 A 时从回路的一端开始，沿着导线行走所遇到的回路中所有电流产生的磁力线总匝数，其中包括了导线中每一部分电流分布的影响。

上图a,b回路的回路自感：

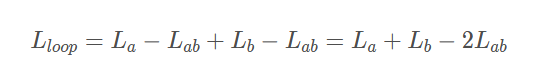
其中：
Lloop​ 表示双引线回路的回路自感
La​ 表示支路a 的局部自感
Lb​ 表示支路b 的局部自感
Lab​ 表示支路a 和b 之间的局部互感

该关系式说明两支路靠得越近，回路电感就越小。其中，各支路的局部自感保持不变，而互感增大，互感增大又使得各支路周围的磁力线总匝数减小，从而回路自感也减小了。

7.有三种重要的特殊几何结构：环形线圈、两条长的并行圆杆和两个宽平板。它们的回路电感有很好的近似公式。

（1）环形线圈
对于环形线圈，其回路电感为：

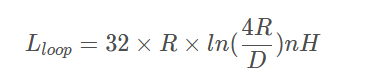
其中：
Lloop​ 表示回路电感，单位为nH
R 表示线圈的半径，单位为in
D 表示构成线圈的导线的直径，单位为m

回路电感并不与面积或圆周长成正比，而是与半径乘以半径的自然对数（即 R×lnR) 成正比。圆周长越大，每一段的局部自感就越大，但同时，回路中相反方向的电流也离得越远，从而它们之间的局部互感就越小。但是，回路电感大致与半径成正比。若圆周长增大，回路电感就会增大。

（2）相邻的双圆感
对于两根相邻的直圆杆，若其中一条为另一条的返回电流路径，则回路电感为：
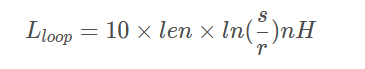其中：

Lloop​ 表示回路电感，单位为 nH
len 表示圆杆长度，单位为 m
r 表示圆杆半径，单位为mil
s 表示两圆杆的中心距，单位为 mil

该关系式说明，两根平行导线的回路电感直接与导线的长度成正比，与中心距的自然对数成正比中心距变大，回路电感也增大，但它是与间距的自然对数成比例，所以变化很缓慢。

以后我们会发现，任何阻抗可控互连线的单位长度回路电感都是恒定的。

8.如果进入芯片的电流发生突变，则当变化的电流流过的电源分配网络的互联阻抗时，就会引起电压降，称为轨道下沉或者轨道塌陷。

9.要使电源分配网络的阻抗比较小，有两条设计原则：
（1）低频时，添加具有低回路电感的去耦电容器；
（2）高频时，使去耦电容器和芯片焊盘之间的回路电感最小，以保持他们之间的阻抗低于一定的值。

10.去耦电容大小怎么定，可以根据时间段△t内，去耦电容必须提供的电荷量大致加以估算：

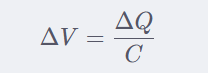
其中：
ΔV 表示电容器两端的电压变化量
ΔQ 表示电容器中减少的电荷桩
C 表示电容器的电容量

那么流经芯片的电流 I 又为多少呢？显然，这主要取决千具体的芯片，并且随着芯片中的代码不同也会有很大的变化。而芯片功耗P 与两端的电压 V 和流经的平均电流有关。

如果给出芯片的平均功耗，则流过芯片的平均电流为：

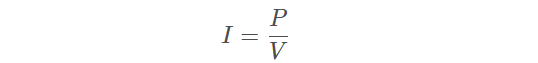
把芯片需要的去耦总量所能提供的去耦时间 Δt 联系起来，即为：

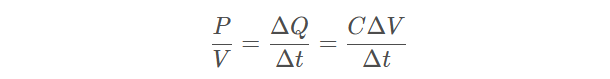
从该关系中，可以得出电容器的去耦时间：

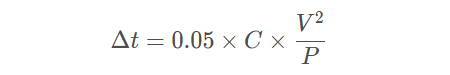
或者，在给定时间内所需要的去耦电容量为：

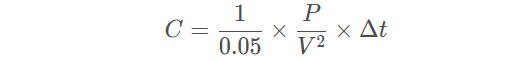
其中：
Δt 表示电荷从电容器逸出的时间，单位为s
0.05 表示允许的 5% 压降
C 表示去耦电容器的电容，单位为 F
V 表示轨道电压，单位为 V
P 表示芯片的功耗，单位为 W

对于实际的电容器，其末端和芯片上焊盘相连的那段连线之间会有相应的回路电感。该回路电感与理想电容元件相串联，导致实际电容器的阻抗随频率的升高而增大。

测量0603去耦电容器的阻抗的曲线图，这是从电容器一端到另一端的回路阻抗，其中经过元件下面的平面。
低频时，就像理想电容器一样，阻抗随频率的增大而减小。但是，随着频率的升高，从某一点起，串联的回路电感开始在阻抗中起主导作用。该点的频率称为自谐振频率，此后阻抗开始增大。频率大于自谐振频率时，电容器的阻抗与电容量完全无关，只与相应的回路电感有关。所以在频率较高时，如果想减小去耦电容器的阻抗，就要减小与之相关的回路电感，而不是增大电容量。
去耦电容器的一个重要特性就是在频率较高时，阻抗仅与回路电感有关，此电感称为等效串联电感(ESL)。

高频时，减小去耦电容的阻抗的唯一方法就是减小它的回路自感。

11.减小回路电感的方法：

（1）使电源平面和地平面靠近电路板表面层以缩短过孔；
（2）使用尺寸较小的电容器；
（3）从电容器焊盘到过孔间的连线要尽措短；
（4）将多个电容器并联使用。

12.每方块回路电感：
由两个平面构成电流路径的回路电感，取决于每个平面路径的局部自感和他们之间的局部互感。

平面越长，局部自感就越大，从而回路电感也就越大。
对于宽导体．宽度w远大于它们的间距 h, 即 w>>b , 两平面间的回路电感可以很精确地近似为：

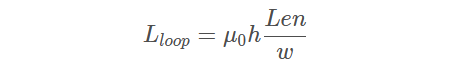
其中
Lloop​ 表示回路电感，单位为 nH
μ0​ 表示自由空间的导磁率，为 32 nH/mil
h 表示平面间距，单位为 mil
Len 表示平面的长度单位为 mil
w 表示平而的宽度． 单位为 mil

电源平面和地平面尽可能地靠近可以减小平面的回路电感，同时减小轨道塌陷和EMI。

13.平面间的回路电感增大是由于过孔约束电流的流动形成了很高的电流密度。对电流流动的约束越大，局部自感和回路电感就越大。有时候把回路增加的电感称为扩散电感(spreading inductance)。如果接触面积增大，电流密度就会降低扩散电感也会减小。

对于连接有许多电容和封装引线的一对平面，若使用多对过孔来传导电流，则减小平面间距可以减小所有同时电流突变 (dI/dt) 产生的压降。

对于有去耦电容的平面，其回路电感是由扩散电感决定的，而不是取决于芯片和电容间的距离。 当然，去耦电容的总回路电感与它到芯片的距离有点关系。让去耦电容靠近高功耗芯片，可以把返回平面上的高频电流限制在芯片附近，并使之远离电路板上的 I/O 端口区域，这样就能使驱动外部电缆中共模电流和引起 EMI 的地弹电压噪声减小。

14.出砂孔： ANTI-PAD 反焊盘：

出砂孔会使平面的回路电感增大。我们经常听说封装下面的出砂孔阵列一一钮扣状器件的散应，会使平而的回路电感显著增大，而要知道增加了多少，惟一的方法就是使用场求解器。

但没有想象的那么严重，回路电感的增加仍可控在两倍以内。

15.回路互感产生的噪声：
若有两个相互独立的电流回路，那么它们之间就会产生互感。回路互感就是第一条回路中有 1 A 电流通过时，它所产生的环绕在第一条回路周围的磁力线匝数。

当第一条回路中的电流发生变化时，环绕在第二条回路周围的磁力线匝数就会改变而且还会产牛噪声，值为：

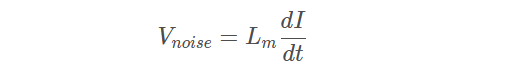
其中:
Vnoise​ 表示产生的电压噪声
Lm​ 表示两问路之间的回路庄感
dI/dt 表示第二条回路电流的变化率

只有当动态同路中的电流变化时，在静态回路中才会产生噪声, 而且这种情况仅在开关跳变时才发生这就是该类噪声经常称为开关噪声，同时开关噪声(SSN) 或ΔI 噪声的原因。

互感会引起两条均匀传输线之间的串扰。

16.多个电感器：
（1）串联：局部电感串联，等效自感：

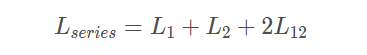
（2）并联：元件并联连接时，等效的局部自感为：

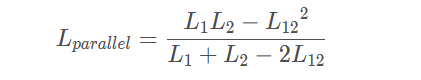
其中：
Lseries​ 表示串联的等效局部自感
Lparallel​ 表示并联的等效局部自感
L1​ 表示其中一个元件的局部自感
L2​ 表示另一个元件的局部自感
L12​ 表示两元件间的局部互感

当局部互惑为零且局部自感相同时，上述关系式简化为我们所熟悉的表达式，即串联的等效电感是其中一个局部自感的2 倍，并联的等效电感是其中一个局部自感的1/2 。

对于两导线的局部自感相同这种特殊情况，串联的等效电感就是其中一个自感与互感之和的2 倍，而并联的等效电感为：

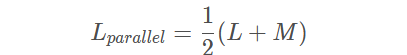
其中：
Lparallel​表示并联的等效局部自感
L 表示单个元件的局部自感
M 表示两元件间的局部互感

从上式可以看出，如果要减小两条并联电流路径的等效电感，只要元件间的互感减小了，其等效电感就会减小。

17.当导线中流过单位安培电流时，与电流分布在外表面相比，电流集中在圆柱杆中心时有更多的磁力线和 更大的自感。

18.电感最大的电流路径，其阻抗也最大；随着频率的升高，高电感路径的阻抗会变得更大。频率越高电流越倾向于选择电感较低的路径，即趋向于圆柱杆表面的路径。

19.趋肤效应： 一般来说，频率越高，电流越是趋向于在导线的外表面上流动。在某一给定频率，从导线内部到外部表面有特定的电流分布， 这取决于电阻与感性阻抗的相对大小电流密度越大的地方。电阻性阻抗上的压降就越高但是频率越高，内部路径和外部路径的，感性阻抗的差别就越大。这种较员恁味着电流分布随频率而变化，且在高频时，全部电流会趋向导体表面的那一薄层。

在这种几何结构中． 可以把电流层近似成有固定厚度 δ 的均匀分布．片称该等仪厚度为趋肤深度，它取决于频率、金属的电导率和导磁率：

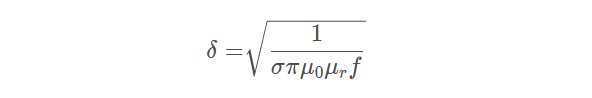
其中：

δ 表示趋肤深度，单位为m ( 米）
σ 表示金属的电导率，单位为S/m
μ0​ 表示自由空间的导磁率，为4π × 10-7 H/m
μr​ 表示导线的相对导磁率
f 表示正弦波频率，单位为Hz

铜的电导率为5.6 x 10-7 S/m. 相对导磁率为1 . 所以它的趋肤深度近似为：
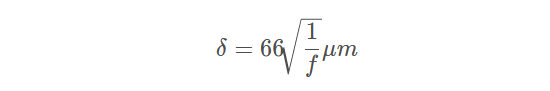f 表示正弦波频率，单位为Hz。
1 盎司铜微带线中的电流分布：在1MHz时，电流儿乎是均匀分布的。10MHz时，电流开始重新分布。高于10MHz 时，趋肤深度远小于横截面的几何厚度并开始主导电流分布。两个例子中，在频率较高时电流都会重新分布以尽可能减小阻抗。随着频率的升高，导线的体电阻率不变。就铜而言，直到频率大于100GHz 时，电阻率才开始发生变化。然而，如果由于趋肤效应的影响而使电流流过的横截面很薄，则互连线的电阻就会增大。

20.提到微带线的回路自感，通常是指所有电流都在外表面的高频界限情况。如果电流靠近导线表面而且与导线几何厚度无关，这一频率就是趋肤效应的界限，“高频”是指高于这一界限的频率。

21.超过趋肤深度极限时，回路电感几乎仅由外部磁力线构成，所以铁磁体导线中的高频信号感受到的回路电感与铜导线的回路电感大致相当。

22.其中一个导体的电流变化时．第二个导体中会产生感应电流．我们称这种电流为涡流。