电路方案分析(九)±1A 单电源低侧电流感应解决方案参考设计
±1A 单电源低侧电流感应解决方案参考设计
tips:TI设计方案参考分析:TI Designs:TIPD175
1.设计需求
2.理论分析
3.器件选择
4.仿真
5.原理图和PCB设计
电路描述:
这种单电源低侧双向电流传感解决方案可以准确检测从-1 A到1 A的负载电流。输出的线性范围为110 mV至3.19 V。该设计利用了配置为差分放大器和参考电压缓冲器的OPA2313运算放大器。
原理图:
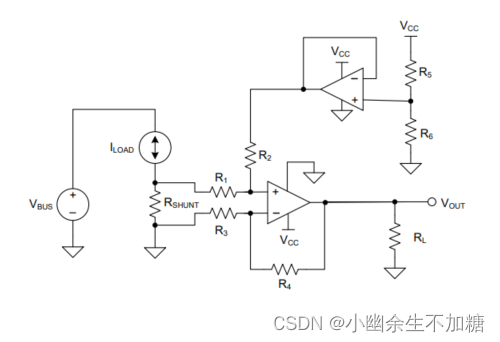
demo板:

1.设计需求
设计需求如下:
(1)3.3V供电;
(2)输入:-1A-1A;
(3)输出:110mV-3.19V;
(4)最大分流电压:±100mV。
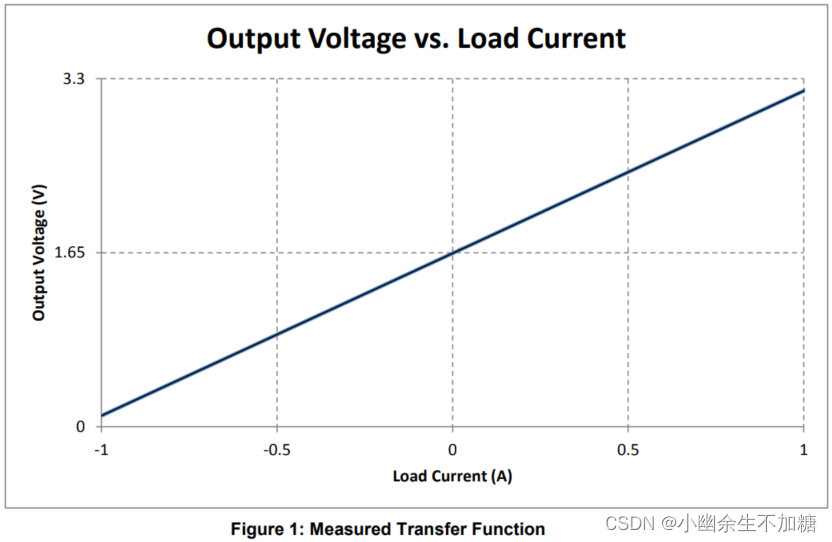
表1总结了设计目标和性能。图1描绘了设计的测量传递函数。

2.理论分析
低侧电流采集测量是理想的,因为共模电压接近地面。因此,电流感测解决方案总是与总线电压VBUS无关。当感测双向电流时,必须添加参考电压以区分正负电流。
图2描绘了用于低侧双向电流采集解决方案的典型电路拓扑结构。当考虑成本优先时,以精度和印刷电路板 (PCB) 空间为代价,这种拓扑结构特别有用。
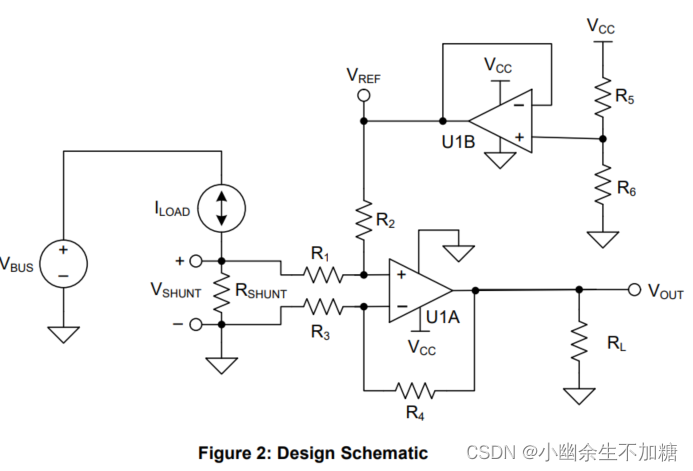
分压电压 (VSHUNT) 流过分压电阻 (RSHUNT:也叫采样电阻) 产生负载电流 (ILOAD) 。VSHUNT由运算放大器 (U1A) 根据R4与R3之比设置的增益进行放大输出。要实现公式 (1) 中的传递函数并使如表2中所述的误差最小化,请设置R4 = R2和R3 = R1。
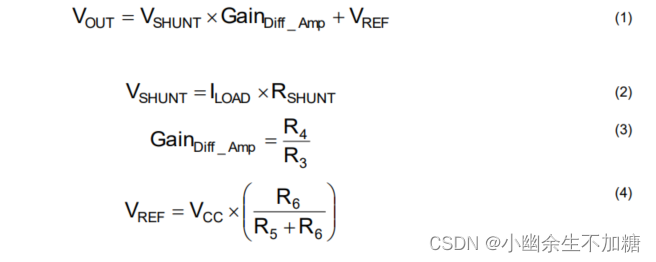
(1)误差分析
图2中的电路引入了两种类型的误差: 偏移和增益。表2列出了误差的来源及其各自的误差类型。

误差处理方法:这些误差最终合并,并在输出端作为增益和偏移误差进行测量结果的输出。通常使用均方根平方和 (RSS) 方法将它们组合在一起。当将误差与正态分布组合时使用此方法,从而产生典型的总误差。对于最坏情况下的总误差,只需要直接添加所有误差项即可。
3.器件选择
(1)采样电阻(RSHUNT)
如上图2所示,VSHUNT的值是系统负载的接地电位。如果VSHUNT的值太大,则在与接地电位真正为0 V的系统接口时可能会引起问题。如果VSHUNT的设置的太过偏负,除了潜在的接口问题外,它还可能违反差分放大器的输入共模电压。
因此,限制采样电阻器两端的电压非常重要。公式 (5) 在给定100 mV的最大分压的情况下计算RSHUNT的最大值。
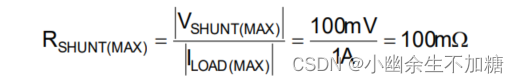
由于成本在该设计中是优先考虑的,因此选择了具有0.5% 容差的电阻器。
(2)运算放大器
该设计中的分流电压可以从-100 mV到100 mV。配置为差分放大器 (U1A) 的运算放大器必须具有包括该电压范围的输入共模信号。
因此,建议使用扩展到GND以下的轨到轨输入 (RRI) 运算放大器。放大器的输出摆幅也应该是轨到轨输出 (RRO),以最大化系统的动态范围。
建议使用CMOS运算放大器,因为电源电压为3.3 V。参考电压运算放大器 (U1B) 应具有低偏移电压。由于此设计中有2个运算放大器,因此双封装可最大程度地减少所需的面积。
此设计利用了OPA2313,因为它是RRI/O CMOS器件。此外,该设备的成本与性能的对比非常出色。
OPA2313是一款1MHz,微功耗,低噪声,轨到轨输出入输出 (RRIO)的运算放大器。

(3)参考电压分压电阻(R5-R6)
由于负载电流范围是对称的 (-1 A至1 A),所以对电源电压进行分压的电阻器应相等,使得参考电压为中间电源 (1.65 V)。由于成本在该设计中是优先考虑的,因此公差应与采样电阻器公差 (0.5%) 一致。最后,选择足够大的电阻器以满足系统的低功耗要求。对于此设计,选择了10 kΩ 电阻。
(4)差分放大器增益设置电阻(R1-R4)
等式 (6) 和 (7) 示出了给定3.3V电源的OPA2313的输入共模和输出电压范围。

增益的计算如式 (8) 所示。
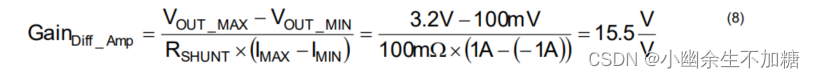
为R1和R3选择的电阻值为1 kΩ。为R2和R4选择的电阻值为15.4 kΩ,这是最接近15.5 kΩ 理想值的0.1% 值。因此,差分放大器的理想增益为15.4 V/V。
4.仿真
(1)传递函数
图3显示了TINA-TI™用于模拟直流传递函数的原理图。
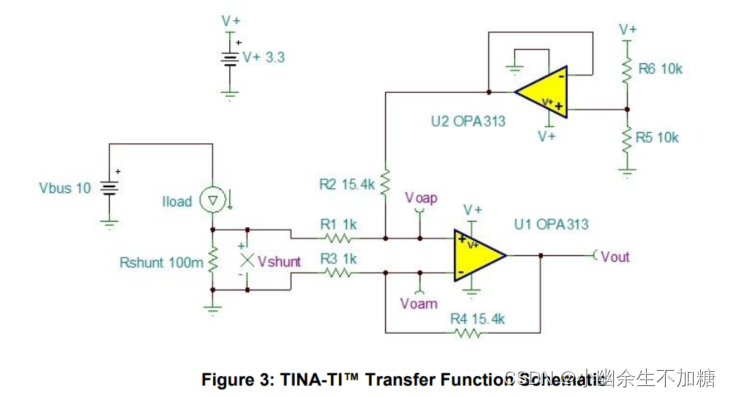
图4描述了使用标称分量值的模拟dc传递函数结果。
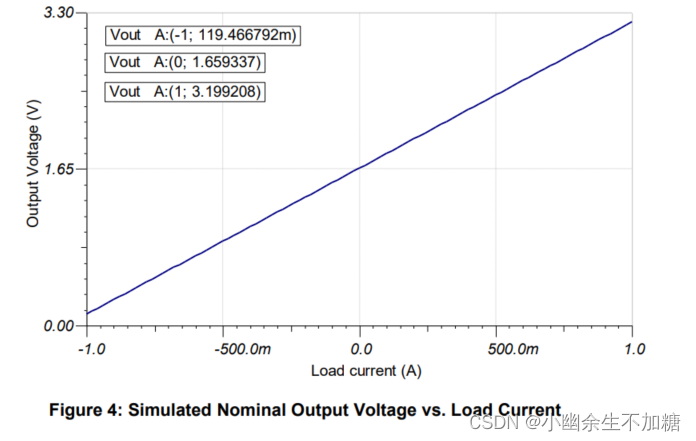
这些结果与公式 (9) 和 (10) 中计算的理想最小和最大输出电压相关。
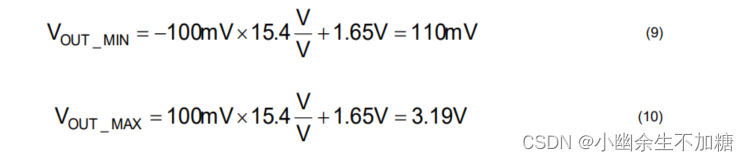
(2)蒙特卡罗模拟误差分析
蒙特卡罗(Monte Carlo)方法,又称随机抽样或统计试验方法,属于计算数学的一个分支,它是在上世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。传统的经验方法由于不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡罗方法由于能够真实地模拟实际物理过程,故解决问题与实际非常符合,可以得到很圆满的结果。这也是以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。
为了分析由于运算放大器、RSHUNT的容差、差分放大器电阻器R1-R4和基准分压器电阻器R5-R6引起的误差,在-1 A和1 A输入电流下运行1,000点蒙特卡罗模拟。蒙特卡罗模拟的结果如表3所示。
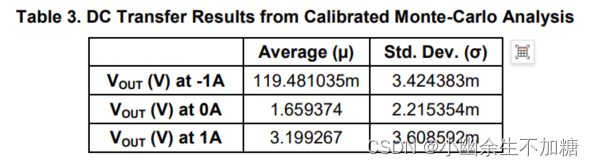
使用蒙特卡罗模拟的平均值 (µ) 和标准偏差 (σ),使用公式 (12) 计算典型 (± 1σ) 偏移误差的预测。
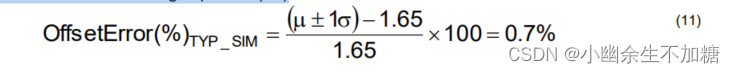
类似地,下面计算典型增益误差的预测。
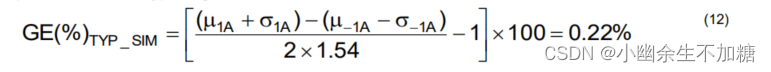
(3)DC扫描误差分析
除了蒙特卡洛模拟之外,还模拟了图3中电路的最坏情况dc扫描,同时在其典型值 (± 1σ) 内改变电阻器,这是其给定容差的1/3。例如,具有0.1% 的公差的电阻器被改变为0.033%。典型的偏移误差被模拟为0.86%,增益误差被0.24%。这些结果与蒙特卡罗模拟有很好的相关性。
(4)仿真结果
表4将仿真结果与设计目标进行了比较。

5.原理图PCB设计
(1)原理图设计
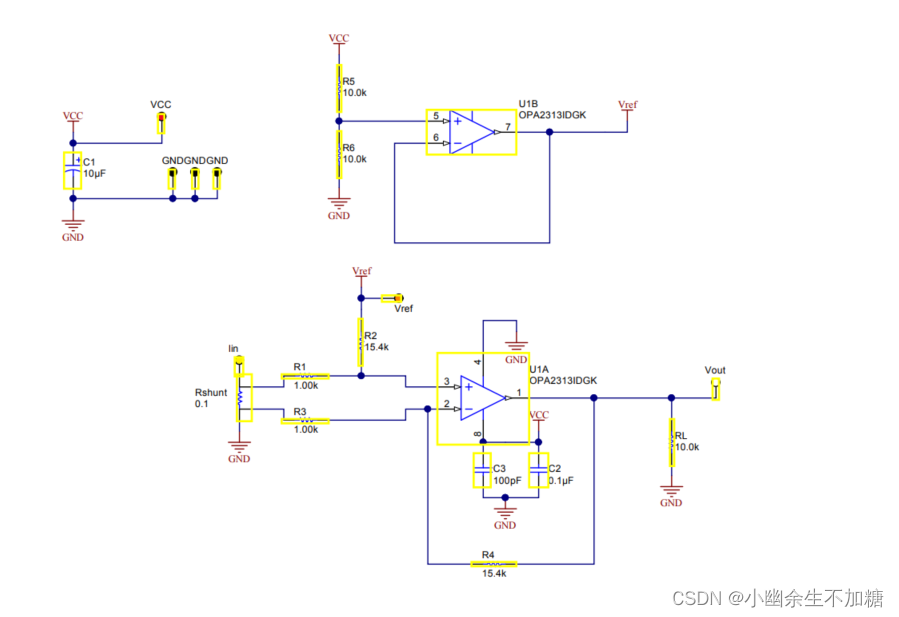
(2)PCB设计
如图所示描绘了印刷电路板 (PCB) 的布局。分流电压的迹线平衡且短。宽而短的迹线用于负载电流路径,以最大程度地减少阻抗。观察到所有其他标准PCB布局做法。