【机器学习】ID3算法构建决策树
ID3算法
ID3 提出了初步的决策树算法;C4.5 提出了完整的决策树算法;CART (Classification And Regression Tree) 目前使用最多的决策树算法;
1、ID3 算法
ID3 算法是决策树的经典构造算法，内部使用信息熵和信息增益来进行构建，每次迭代算则信息增益最大的特征属性作为分割属性。
优点:决策树构建速度快，实现简单。
缺点:计算依赖于特征数目较多的特征，而属性值最多的属性并不一定最优。ID3算法不是递增算法。ID3算法是单变量决策树，对于特征属性之间的关系不会考虑。抗噪性差。数据集中噪音点多可能会出现过拟合。只适合小规模的数据集，需要将数据放到内存中。
2、C4.5 算法
C4.5 算法是在ID3算法上的优化。使用信息增益率来取代ID3中的信息增益，在树的构造过程中会进行剪枝操作进行优化，能够自动完成对连续属性的离散化处理。
ID3当时构建的时候就没有去考虑连续值这个问题。
C4.5 算法在选中分割属性的时候选择信息增益率大的属性，公式如下:
优点:产生规则易于理解。准确率较高。(因为考虑了连续值，数据越多拟合程度就越好。)实现简单。
缺点:对数据集需要进行多次扫描和排序，所以效率较低。(比如之前例子中收入的连续值，分割次数越多，需要扫描的次数也就越多，排序次数也越多。)只适合小规模数据集，需要将数据放到内存中。
3、CART算法
使用基尼系数Gain作为数据纯度的量化指标来构建决策树算法，叫做CART算法。
GINI增益作为分割属性选择的标准，选择GINI增益最大的作为当前数据集分割属性。可以用于分类和回归两类问题。
注意:CART构建的是二叉树。
4、总结
1、ID3和C4.5算法只适合小规模数据集上使用。2、ID3和C4.5算法都是单变量决策树。3、当属性值比较多的时候请使用C4.5。4、决策树分类一般情况只适合小数据量的情况(数据可以放内存)5、CART算法是最常用的一种决策树构建算法。6、三种算法的区别只是对于当前树的评价标准不同而已，ID3使用信息增益，C4.5使用信息增益率，CART使用基尼系数。7、CART算法构建的一定是二叉树。
构建决策树三个重要的问题
（1）数据是怎么分裂的
（2）如何选择分类的属性
（3）什么时候停止分裂
从上述三个问题出发，以实际的例子对ID3算法进行阐述。
例：通过当天的天气、温度、湿度和季节预测明天的天气
表1 原始数据
|
当天天气 |
温度 |
湿度 |
季节 |
明天天气 |
|
晴 |
25 |
50 |
春天 |
晴 |
|
阴 |
21 |
48 |
春天 |
阴 |
|
阴 |
18 |
70 |
春天 |
雨 |
|
晴 |
28 |
41 |
夏天 |
晴 |
|
雨 |
8 |
65 |
冬天 |
阴 |
|
晴 |
18 |
43 |
夏天 |
晴 |
|
阴 |
24 |
56 |
秋天 |
晴 |
|
雨 |
18 |
76 |
秋天 |
阴 |
|
雨 |
31 |
61 |
夏天 |
晴 |
|
阴 |
6 |
43 |
冬天 |
雨 |
|
晴 |
15 |
55 |
秋天 |
阴 |
|
雨 |
4 |
58 |
冬天 |
雨 |
1.数据分割
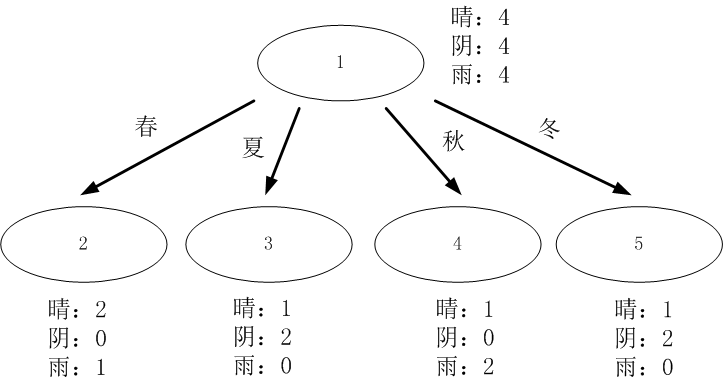
对于离散型数据，直接按照离散数据的取值进行分裂，每一个取值对应一个子节点，以“当前天气”为例对数据进行分割，如图1所示。
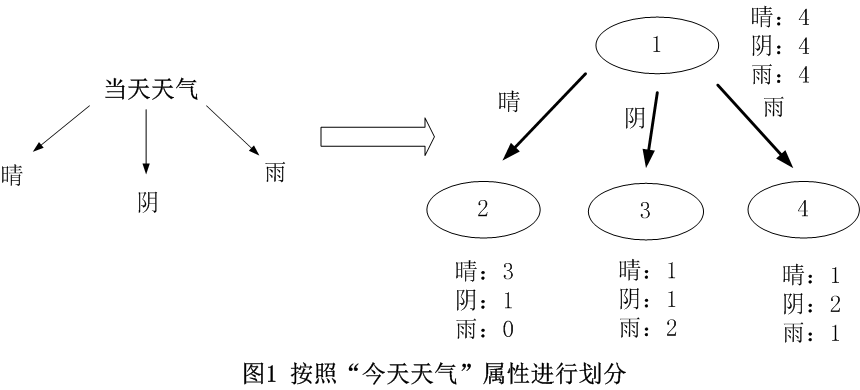
对于连续型数据，ID3原本是没有处理能力的，只有通过离散化将连续性数据转化成离散型数据再进行处理。
连续数据离散化是另外一个课题，本文不深入阐述，这里直接采用等距离数据划分的李算话方法。该方法先对数据进行排序，然后将连续型数据划分为多个区间，并使每一个区间的数据量基本相同，以温度为例对数据进行分割，如图2所示。
2. 选择最优分裂属性
ID3采用信息增益作为选择最优的分裂属性的方法，选择熵作为衡量节点纯度的标准，信息增益的计算公式如下：
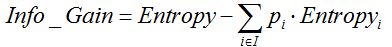
其中， 
表示父节点的熵； 
表示节点i的熵，熵越大，节点的信息量越多，越不纯； 
表示子节点i的数据量与父节点数据量之比。 
越大，表示分裂后的熵越小，子节点变得越纯，分类的效果越好，因此选择 最大的属性作为分裂属性。
对上述的例子的跟节点进行分裂，分别计算每一个属性的信息增益，选择信息增益最大的属性进行分裂。
天气属性：（数据分割如上图1所示）
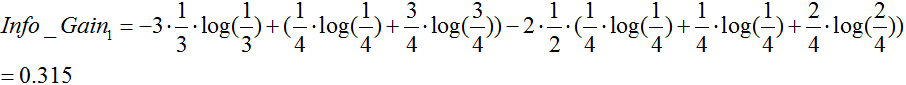
温度：（数据分割如上图2所示）
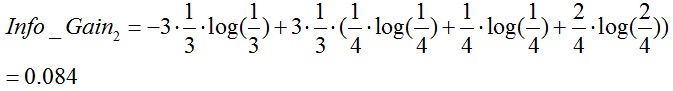
湿度：
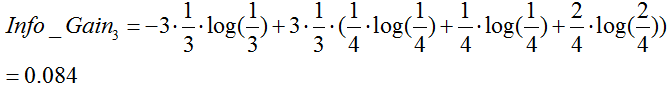
季节：
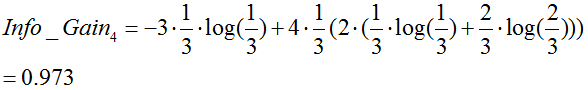
由于
最大，所以选择属性“季节”作为根节点的分裂属性。
如何使用Python计算信息熵
#输入参数： #dataSet： 数据集 def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts ={} #遍历数据集中每一个样本 for featVec in dataSet: #取每一个样本的类别标签 currentLabel = featVec[-1] #判断这个标签在字典中是否存在，不存在就初始化 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 #统计不同类别的数量 labelCounts[currentLabel] += 1 #初始化熵 shannonEnt = 0.0 #计算熵 for key in labelCounts: prob = float(labelCounts[key])/numEntries shannonEnt -= prob * log(prob,2) return shannonEnt
3.停止分裂的条件
停止分裂的条件已经在决策树中阐述，这里不再进行阐述。
（1）最小节点数
当节点的数据量小于一个指定的数量时，不继续分裂。两个原因：一是数据量较少时，再做分裂容易强化噪声数据的作用；二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
（2）熵或者基尼值小于阀值。
由上述可知，熵和基尼值的大小表示数据的复杂程度，当熵或者基尼值过小时，表示数据的纯度比较大，如果熵或者基尼值小于一定程度时，节点停止分裂。
（3）决策树的深度达到指定的条件
节点的深度可以理解为节点与决策树跟节点的距离，如根节点的子节点的深度为1，因为这些节点与跟节点的距离为1，子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度，当深度到达指定的上限大小时，停止分裂。
（4）所有特征已经使用完毕，不能继续进行分裂。
被动式停止分裂的条件，当已经没有可分的属性时，直接将当前节点设置为叶子节点。
Python构建决策树
决策树的流程为：
(1)输入需要分类的数据集和类别标签和靶标签。
(2)检验数据集是否只有一列，或者是否最后一列(靶标签数据默认放到最后一列)只有一个水平(唯一值)。
是：返回唯一值水平或者占比最大的那个水平
(3)调用信息增益公式，计算所有节点的信息增益，得到最大信息增益所对应的类别标签。
(4)建立决策树字典用以保存当次叶节点数据信息。
(5)进入循环：
按照该类别标签的不同水平，依次计算子数据集；
对子数据集重复(1),(2),(3),(4),(5), (6)步。
(6)返回决策树字典。
决策树实际上是一个大的递归函数，其结果是一个多层次的字典。
python3实现ID3算法：
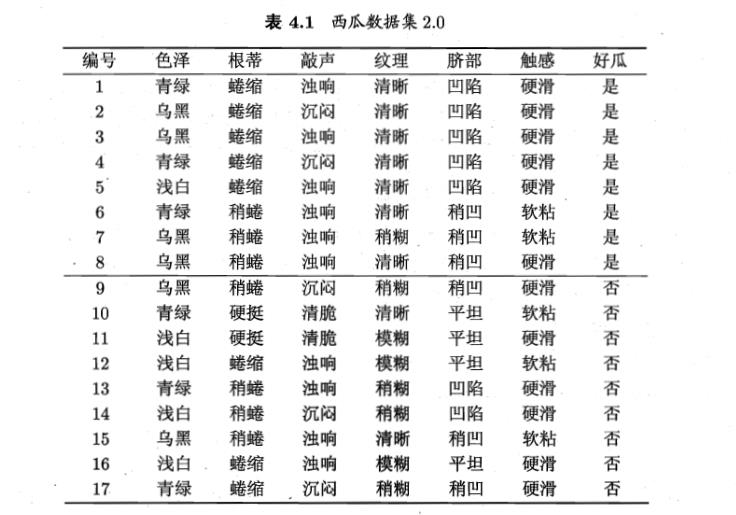
import numpy as np import pandas as pd import json #序列化与反序列树字典 class TreeHandler(object): def __init__(self): self.tree = None def save(self, tree): self.tree = tree with open("tree.txt", mode="w", encoding="utf-8") as f: tree = json.dumps(tree, indent=" ", ensure_ascii=False) f.write(tree) def load(self, file): with open(file, mode="r", encoding="utf-8") as f: tree = f.read() self.tree = json.loads(tree) return self.tree # class ID3Tree(TreeHandler): """主要的数据结构是pandas对象""" __count = 0 def __init__(self): super().__init__() """认定最后一列是标签列""" self.gain = {} def _entropy(self, dataSet): """计算给定数据集的熵""" labels = list(dataSet.columns) level_count = dataSet[labels[-1]].value_counts().to_dict() # 统计分类标签不同水平的值 entropy = 0.0 for key, value in level_count.items(): prob = float(value) / dataSet.shape[0] entropy += -prob * np.log2(prob) return entropy def _split_dataSet(self, dataSet, column, level): """根据给定的column和其level来获取子数据集""" subdata = dataSet[dataSet[column] == level] del subdata[column] # 删除这个划分字段列 return subdata.reset_index(drop=True) # 重建索引 def _best_split(self, dataSet): """计算每个分类标签的信息增益""" best_info_gain = 0.0 # 求最大信息增益 best_label = None # 求最大信息增益对应的标签(字段) labels = list(dataSet.columns)[: -1] # 不包括最后一个靶标签 init_entropy = self._entropy(dataSet) # 先求靶标签的香农熵 for _, label in enumerate(labels): # 根据该label(也即column字段)的唯一值(levels)来切割成不同子数据集，并求它们的香农熵 levels = dataSet[label].unique().tolist() # 获取该分类标签的不同level label_entropy = 0.0 # 用于累加各水平的信息熵；分类标签的信息熵等于该分类标签的各水平信息熵与其概率积的和。 for level in levels: # 循环计算不同水平的信息熵 level_data = dataSet[dataSet[label] == level] # 获取该水平的数据集 prob = level_data.shape[0] / dataSet.shape[0] # 计算该水平的数据集在总数据集的占比 # 计算香农熵，并更新到label_entropy中 label_entropy += prob * self._entropy(level_data) # _entropy用于计算香农熵 # 计算信息增益 info_gain = init_entropy - label_entropy # 代码至此，已经能够循环计算每个分类标签的信息增益 # 用best_info_gain来取info_gain的最大值，并获取对应的分类标签 if info_gain > best_info_gain: best_info_gain = info_gain best_label = label # 这里保存一下每一次计算的信息增益，便于查看和检查错误 self.gain.setdefault(self.__count, {}) # 建立本次函数调用时的字段，设其value为字典 self.gain[self.__count][label] = info_gain # 把本次函数调用时计算的各个标签数据存到字典里 self.__count += 1 return best_label def _top_amount_level(self, target_list): class_count = target_list.value_counts().to_dict() # 计算靶标签的不同水平的样本量，并转化为字典 # 字典的items方法可以将键值对转成[(), (), ...]，可以使用列表方法 sorted_class_count = sorted(class_count.items(), key=lambda x: x[1], reverse=True) return sorted_class_count[0][0] def mktree(self, dataSet): """创建决策树""" target_list = dataSet.iloc[:, -1] # target_list 靶标签的那一列数据 # 程序终止条件一: 靶标签(数据集的最后一列因变量)在该数据集上只有一个水平，返回该水平 if target_list.unique().shape[0] <= 1: return target_list[0] # ！！！ # 程序终止条件二: 数据集只剩下把标签这一列数据；返回数量最多的水平 if dataSet.shape[1] == 1: return self._top_amount_level(target_list) # 不满足终止条件时，做如下递归处理 # 1.选择最佳分类标签 best_label = self._best_split(dataSet) # 2.递归计算最佳分类标签的不同水平的子数据集的信息增益 # 各个子数据集的最佳分类标签的不同水平... # ... # 直至递归结束 best_label_levels = dataSet[best_label].unique().tolist() tree = {best_label: {}} # 生成字典，用于保存树状分类信息；这里不能用self.tree = {}存储 for level in best_label_levels: level_subdata = self._split_dataSet(dataSet, best_label, level) # 获取该水平的子数据集 tree[best_label][level] = self.mktree(level_subdata) # 返回结果 return tree def predict(self, tree, labels, test_sample): """ 对单个样本进行分类 tree: 训练的字典 labels: 除去最后一列的其它字段 test_sample: 需要分类的一行记录数据 """ classLabel = None firstStr = list(tree.keys())[0] # tree字典里找到第一个用于分类键值对 secondDict = tree[firstStr] featIndex = labels.index(firstStr) # 找到第一个建(label)在给定label的索引 for key in secondDict.keys(): if test_sample[featIndex] == key: # 找到test_sample在当前label下的值 if secondDict[key].__class__.__name__ == "dict": classLabel = self.predict(secondDict[key], labels, test_sample) else: classLabel = secondDict[key] return classLabel def _unit_test(self): """用于测试_entropy函数""" data = [ ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], # 1 ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'], # 2 ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], # 3 ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'], # 4 ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], # 5 ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '是'], # 6 ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '是'], # 7 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '是'], # 8 ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '否'], # 9 ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '否'], # 10 ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '否'], # 11 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '否'], # 12 ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '否'], # 13 ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '否'], # 14 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '否'], # 15 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '否'], # 16 ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '否'], # 17 ] data = pd.DataFrame(data=data, columns=['色泽','根蒂','敲声','纹理','脐部','触感','分类']) # return data # 到此行，用于测试_entropy # return self._split_dataSet(data, "a", 1) # 到此行，用于测试_split_dataSet # return self._best_split(data) # 到此行，用于测试_best_split # return self.mktree(self.dataSet) # 到此行，用于测试主程序mktree # 生成树 self.tree = self.mktree(data) # 到此行，用于测试主程序mktree #打印树 print(self.tree) labels = ['色泽','根蒂','敲声','纹理','脐部','触感'] #测试样本 test_sample = ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑'] #预测结果 outcome = self.predict(self.tree, labels, test_sample) print("The truth class is %s, The ID3Tree outcome is %s." % ("否", outcome)) model = ID3Tree() model._unit_test()
数据来源：《机器学习—周志华》
使用matplotlib画出决策树：
import matplotlib.pyplot as plt from pylab import * mpl.rcParams['font.sans-serif'] = ['SimHei'] plt.figure(1, figsize=(8,8)) ax = plt.subplot(111) def drawNode(text, startX, startY, endX, endY, ann): #绘制带箭头的文本 ax.annotate(text, xy=(startX+0.01, startY), xycoords='data', xytext=(endX, endY), textcoords='data', arrowprops=dict(arrowstyle="<-", connectionstyle="arc3"), bbox=dict(boxstyle="square", fc="r") ) #在箭头中间位置标记数字 ax.text((startX+endX)/2, (startY+endY)/2, str(ann)) #绘制树根 bbox_props = dict(boxstyle="square,pad=0.3", fc="cyan", ec="b", lw=2) ax.text(0.5, 0.97, '纹理', bbox=bbox_props) #绘制其他节点 drawNode('根蒂', 0.5, 0.97, 0.25, 0.8, "清晰") drawNode('触感', 0.5, 0.97, 0.50, 0.8, "稍糊") drawNode('坏瓜', 0.5, 0.8, 0.4, 0.65, "硬滑") drawNode('好瓜', 0.5, 0.8, 0.6, 0.65, "硬滑") drawNode('坏瓜', 0.5, 0.97, 0.75, 0.8, "模糊") drawNode('好瓜', 0.25, 0.8, 0.1, 0.65, "蜷缩") drawNode('色泽', 0.25, 0.8, 0.2, 0.65, "稍蜷") drawNode('好瓜', 0.25, 0.8, 0.3, 0.65, "硬挺") drawNode('好瓜', 0.2, 0.65, 0.1, 0.5, "青绿") drawNode('触感', 0.2, 0.65, 0.25, 0.5, "乌黑") drawNode('好瓜', 0.25, 0.5, 0.1, 0.35, "硬滑") drawNode('坏瓜', 0.25, 0.5, 0.4, 0.35, "软粘") #显示图形 plt.show()
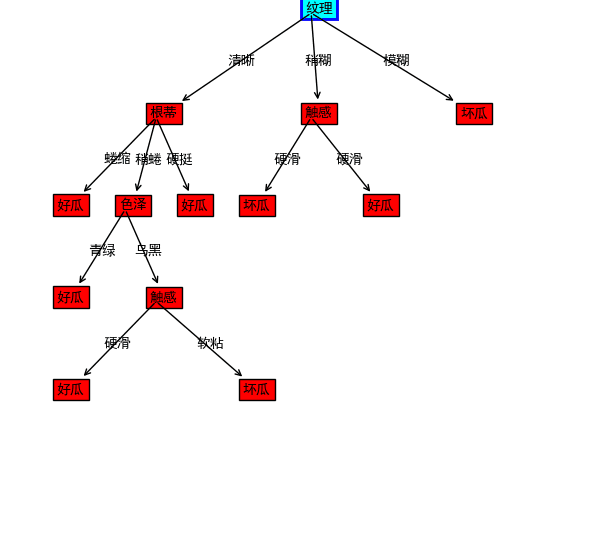
总结
ID3是基本的决策树构建算法，作为决策树经典的构建算法，其具有结构简单、清晰易懂的特点。虽然ID3比较灵活方便，但是有以下几个缺点：
（1）采用信息增益进行分裂，分裂的精确度可能没有采用信息增益率进行分裂高。
（2）不能处理连续型数据，只能通过离散化将连续性数据转化为离散型数据。
（3）不能处理缺省值。
（4）没有对决策树进行剪枝处理，很可能会出现过拟合的问题。
原文摘录：
