连续属性离散化处理
原文链接:https://zhuanlan.zhihu.com/p/63990922
一、概念
某些分类算法,要求我们对连续性的属性进行分类处理,离散化的过程主要包括确定分类的个数,并将数据集映射到这些分类中,这里涉及三种分类方法:
1)等宽法
类似于制作频数分布图,将属性分布值分为几个等分的分布区间;
2)等频法
将相同数量的记录放入每个区间;
3)基于聚类的分析方法
将属性按照K-means算法进行聚类,然后根据聚类的分类,将同一聚类的记录合并到同一组内。
下面针对:肝气郁结证型系数数据集进行三种离散化的python实现,数据集下载地址:
https://github.com/zakkitao/database/blob/master/discretization_data.xls
二、代码实现
1)导入数据集以及各种需要的库
import pandas as pd import matplotlib.pyplot as plt data = 'chapter4/demo/data/discretization_data.xls' data = pd.read_excel(data) import numpy as np
2)等宽离散法
data = data[u'肝气郁结证型系数'].copy() #将数据集转化为集合 k = 4 #k值为组数 d1 = pd.cut(data,k,labels=range(k)) #将集合分组
3)等频离散法
w = [i/k for i in range(k+1)] #计算百分比 w = data.describe(percentiles=w)[4:9] #计算各个百分位数 d2 = pd.cut(data,w,labels=range(k)) #将集合分组
4)k-means分组
from sklearn.cluster import KMeans #导入kmeans kmodel = KMeans(n_clusters = k) #确定族数 kmodel.fit(data.values.reshape(len(data),1)) #训练数据集 c = pd.DataFrame(np.sort(kmodel.cluster_centers_)) #确定中心并排序 w = c.rolling(2).mean().iloc[1:] #取移动平均值 w = [0]+list(w[0])+[data.max()] #加上最大最小值作为边界值 w = list(np.sort(w)) #再次排序 d3 = pd.cut(data,w,labels = range(k))
5)定义画图函数并生成图像
def classified_plot(d): plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False plt.figure(figsize=(7,5)) for j in range(0, k): plt.plot(data[d==j], [i for i in d[d==j]], 'o') classified_plot(d1) classified_plot(d2) classified_plot(d3)
如图:按照顺序排列的三图
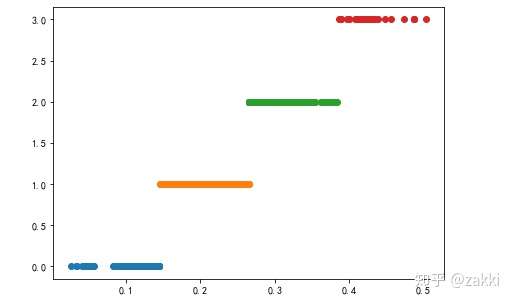
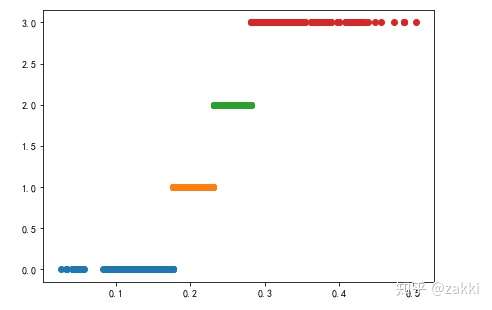
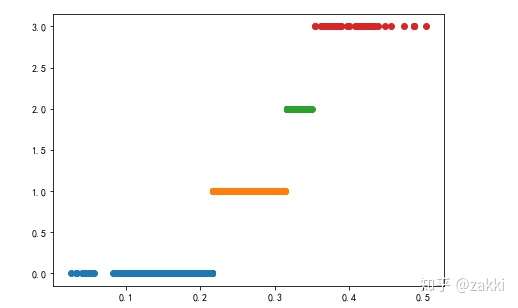


 浙公网安备 33010602011771号
浙公网安备 33010602011771号