PID应用详解
PID应用详解
阅读目录
1.PID介绍及原理
2.常用四轴的两种PID算法讲解(单环PID、串级PID)
3.常用PID算法的C语言实现
5.常用的四轴飞行器PID算法
PID介绍及原理
PID介绍
在工业应用中PID及其衍生算法是应用最广泛的算法之一，是当之无愧的万能算法，也是最经典的算法。
现在已经演变出很多智能的算法，如蚁群，神经网络等，感兴趣可以看一下刘金琨老师的《先进pid控制》
PID算法的一般形式：
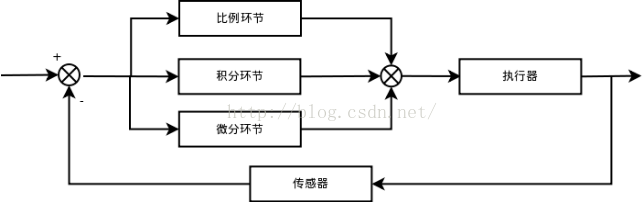
通过误差信号控制被控量，而控制器本身就是比例、积分、微分三个环节的加和。这里我们规定（在t时刻）：
1.输入量为rin(t);
2.输出量为rout(t);
3.偏差量为err(t)=rin(t)-rout(t);
pid的控制规律为：偏差控制被控制量
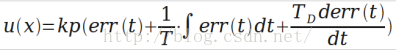
1.说明一下反馈控制的原理，通过上面的框图不难看出，PID控制其实是对偏差的控制过程;
2.如果偏差为0,则比例环节不起作用，只有存在偏差时，比例环节才起作用。
3.积分环节主要是用来消除静差，所谓静差，就是系统稳定后输出值和设定值之间的差值，积分环节实际上就是偏差累计的过程，把累计的误差加到原有系统上以抵消系统造成的静差。
4.而微分信号则反应了偏差信号的变化规律，或者说是变化趋势，根据偏差信号的变化趋势来进行超前调节，从而增加了系统的快速性。
PID原理普及
1、 对自动控制系统的基本要求：稳、准、快：
- 稳定性（P和I降低系统稳定性，D提高系统稳定性）：在平衡状态下，系统受到某个干扰后，经过一段时间其被控量可以达到某一稳定状态；
- 准确性（P和I提高稳态精度，D无作用）：系统处于稳态时，其稳态误差；
- 快速性（P和D提高响应速度，I降低响应速度）：系统对动态响应的要求。一般由过渡时间的长短来衡量。
2、 稳定性：当系统处于平衡状态时，受到某一干扰作用后，如果系统输出能够恢复到原来的稳态值，那么系统就是稳定的；否则，系统不稳定。
3、 动态特性（暂态特性，由于系统惯性引起）：系统突加给定量（或者负载突然变化）时，其系统输出的动态响应曲线。延迟时间、上升时间、峰值时间、调节时间、超调量和振荡次数。
通常：
- 上升时间和峰值时间用来评价系统的响应速度；
- 超调量用来评价系统的阻尼程度；
- 调节时间同时反应响应速度和阻尼程度；
4、 稳态特性：在参考信号输出下，经过无穷时间，其系统输出与参考信号的误差。影响因素：系统结构、参数和输入量的形式等
5、 比例（P）控制规律：具有P控制的系统，其稳态误差可通过P控制器的增益Kp来调整：Kp越大，稳态误差越小；反之，稳态误差越大。但是Kp越大，其系统的稳定性会降低。
由上式可知，控制器的输出m(t)与输入误差信号e(t)成比例关系，偏差减小的速度取决于比例系数Kp：Kp越大，偏差减小的越快，但是很容易引起振荡（尤其是在前向通道中存在较大的时滞环节时）；Kp减小，发生振荡的可能性小，但是调节速度变慢。单纯的P控制无法消除稳态误差，所以必须要引入积分I控制。原因：（R为参考输入信号，Kv为开环增益）
当参考输入信号R不为0时，其稳态误差只能趋近于0，不能等于0。因为开环增益Kv不为0。
6、 比例微分（PD）控制规律：可以反应输入信号的变化趋势，具有某种预见性，可为系统引进一个有效的早期修正信号，以增加系统的阻尼程度，而从提高系统的稳定性。（tao为微分时间常数）
如果系统中存在较大时滞的环节，则输出变化总是落后于当前误差的变化，解决的方法就是使抑制误差的作用变化“超前”，增强系统的稳定性。
7、 积分（I）控制规律：由于采用了积分环节，若当前误差e(t)为0，则其输出信号m(t)有可能是一个不为0的常量。需要注意的是，引入积分环节，可以提到系统型别，使得系统可以跟踪更高阶次的输入信号，以消除稳态误差。
8、 比例积分（PI）控制规律：在保证系统稳定的前提下，引入PI控制器可以提高它的稳态控制质量，消除其稳态误差。（ti为积分时间常数）
积分调节可以消除静差，但有滞后现象，比例调节没有滞后现象，但存在静差。 PI调节就是综合P、I两种调节的优点，利用P调节快速抵消干扰的影响，同时利用I调节消除残差。
9、 比例积分微分（PID）控制规律：除了积分环节提高了系统型别，微分环节提高了系统的动态性能。
观察PID的公式可以发现：Kp乘以误差e(t)，用以消除当前误差；积分项系数Ki乘以误差e(t)的积分，用于消除历史误差积累，可以达到无差调节；微分项系数Kd乘以误差e(t)的微分，用于消除误差变化，也就是保证误差恒定不变。由此可见，P控制是一个调节系统中的核心，用于消除系统的当前误差，然后，I控制为了消除P控制余留的静态误差而辅助存在，对于D控制，所占的权重最少，只是为了增强系统稳定性，增加系统阻尼程度，修改PI曲线使得超调更少而辅助存在。10、P控制对系统性能的影响：
- 开环增益越大，稳态误差减小（无法消除，属于有差调节）
- 过渡时间缩短
- 稳定程度变差
11、I控制对系统性能的影响：
- 消除系统稳态误差（能够消除静态误差，属于无差调节）
- 稳定程度变
12、D控制对系统性能的影响：
- 减小超调量
- 减小调节时间（与P控制相比较而言）
- 增强系统稳定性
- 增加系统阻尼程
13、PD控制对系统性能的影响：
- 减小调节时间
- 减小超调量
- 增大系统阻尼，增强系统稳定性
- 增加高频干
14、PI控制对系统性能的影响：
- 提高系统型别，减少系统稳态误差
- 增强系统抗高频干扰能力
- 调节时间增大
15、P调节、I调节降低系统稳定性 D调节增强系统稳定性 所以PI调节器的P比P调节器的P要小一些，PD调节器的P比P调节器的P要大一些16、位置式PID表达式（数字PID）：
P(n)为第n次输出，e(n)为第n次偏差值，Ts为系统采用周期，Ti为积分时间常数，Td为微分时间常数
16、消除随机干扰的措施：
- 几个采样时刻的采样值求平均后代替本次的采样值
- 微分项的四点中心差分(e(n)-e(n-3)+3e(n-1)-3e(n-2))*1/(6Ts)
- 矩形积分改为梯形积分
常用四轴的两种PID算法讲解(单环PID、串级PID)
单环PID
这里主要讲解的PID算法属于一种线性控制器，这种控制器被广泛应用于四轴上。要控制四轴，显而易见的是控制它的角度，那么最简单，同时也是最容易想到的一种控制策略就是角度单环PID控制器，系统框图如图所示：
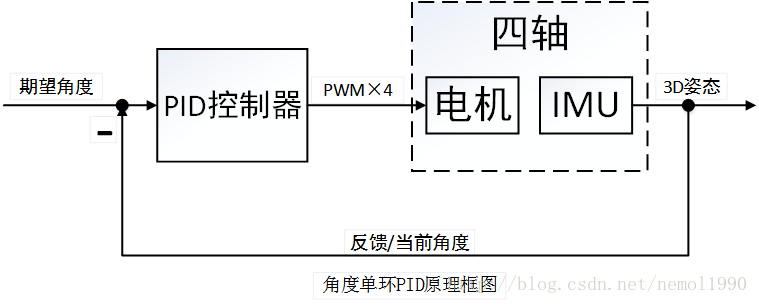
伪代码：
串级PID
上述角度单环PID控制算法仅仅考虑了飞行器的角度信息，如果想增加飞行器的稳定性(增加阻尼)并提高它的控制品质，我们可以进一步的控制它的角速度，于是角度/角速度-串级PID控制算法应运而生。在这里，相信大多数朋友已经初步了解了角度单环PID的原理，但是依旧无法理解串级PID究竟有什么不同。其实很简单：它就是两个PID控制算法，只不过把他们串起来了(更精确的说是套起来)。那这么做有什么用？答案是，它增强了系统的抗干扰性(也就是增强稳定性)，因为有两个控制器控制飞行器，它会比单个控制器控制更多的变量，使得飞行器的适应能力更强。为了更为清晰的讲解串级PID，这里笔者依旧画出串级PID的原理框图，如图所示：
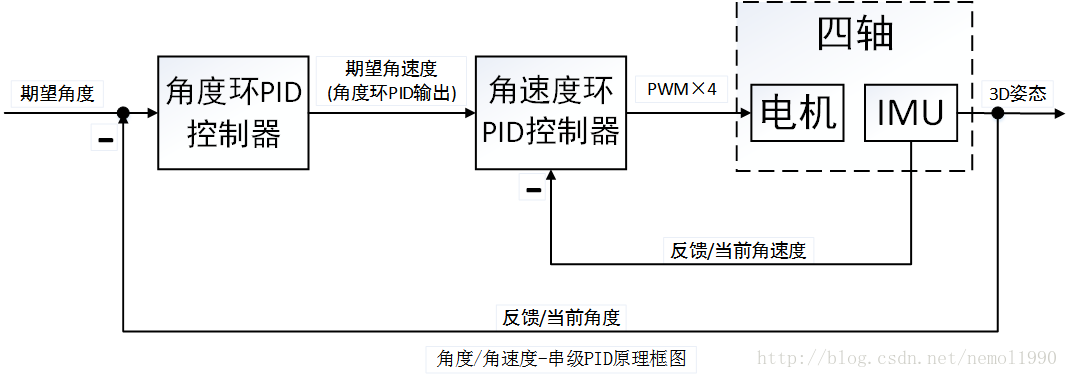
伪代码：
关于如何整定单环PID与串级PID的问题，请原谅笔者的能力有限，无法给出标准而可靠的整定流程，这里我给出三个链接，第一个为阿莫论坛的一位同学的单环PID整定现象与思考，个人觉得参考价值很大；第二、三两个分别为APM与PX4的串级PID整定现象说明，大家可以参考他们的网页说明
而笔者在整定串级PID时的经验则是：先整定内环PID，再整定外环P。
内环P：从小到大，拉动四轴越来越困难，越来越感觉到四轴在抵抗你的拉动；到比较大的数值时，四轴自己会高频震动，肉眼可见，此时拉扯它，它会快速的振荡几下，过几秒钟后稳定；继续增大，不用加人为干扰，自己发散翻机。特别注意：只有内环P的时候，四轴会缓慢的往一个方向下掉，这属于正常现象。这就是系统角速度静差。
内环I：前述PID原理可以看出，积分只是用来消除静差，因此积分项系数个人觉得没必要弄的很大，因为这样做会降低系统稳定性。从小到大，四轴会定在一个位置不动，不再往下掉；继续增加I的值，四轴会不稳定，拉扯一下会自己发散。特别注意：增加I的值，四轴的定角度能力很强，拉动他比较困难，似乎像是在钉钉子一样，但是一旦有强干扰，它就会发散。这是由于积分项太大，拉动一下积分速度快，给 的补偿非常大，因此很难拉动，给人一种很稳定的错觉。
内环D：这里的微分项D为标准的PID原理下的微分项，即本次误差-上次误差。在角速度环中的微分就是角加速度，原本四轴的震动就比较强烈，引起陀螺的值变化较大，此时做微分就更容易引入噪声。因此一般在这里可以适当做一些滑动滤波或者IIR滤波。从小到大，飞机的性能没有多大改变，只是回中的时候更加平稳；继续增加D的值，可以肉眼看到四轴在平衡位置高频震动(或者听到电机发出滋滋的声音)。前述已经说明D项属于辅助性项，因此如果机架的震动较大，D项可以忽略不加。
外环P：当内环PID全部整定完成后，飞机已经可以稳定在某一位置而不动了。此时内环P，从小到大，可以明显看到飞机从倾斜位置慢慢回中，用手拉扯它然后放手，它会慢速回中，达到平衡位置；继续增大P的值，用遥控器给不同的角度给定，可以看到飞机跟踪的速度和响应越来越快；继续增加P的值，飞机变得十分敏感，机动性能越来越强，有发散的趋势。
常用PID算法的C语言实现
位置型PID的C语言实现：
第一步：定义PID变量结构体，代码如下：
struct _pid{
float SetSpeed; //定义设定值
float ActualSpeed; //定义实际值
float err; //定义偏差值
float err_last; //定义上一个偏差值
float Kp,Ki,Kd; //定义比例、积分、微分系数
float voltage; //定义电压值（控制执行器的变量）
float integral; //定义积分值
}pid;
控制算法中所需要用到的参数在一个结构体中统一定义，方便后面的使用。
第二部：初始化变量，代码如下：
void PID_init(){
printf("PID_init begin \n");
pid.SetSpeed=0.0;
pid.ActualSpeed=0.0;
pid.err=0.0;
pid.err_last=0.0;
pid.voltage=0.0;
pid.integral=0.0;
pid.Kp=0.2;
pid.Ki=0.015;
pid.Kd=0.2;
printf("PID_init end \n");
}
统一初始化变量，尤其是Kp,Ki,Kd三个参数，调试过程当中，对于要求的控制效果，可以通过调节这三个量直接进行调节。
第三步：编写控制算法，代码如下：
float PID_realize(float speed){
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
pid.integral+=pid.err;//位置式pid是对积分的持续累加，容易造成积分饱和，是系统过调
pid.voltage=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last);
pid.err_last=pid.err;
pid.ActualSpeed=pid.voltage*1.0;
return pid.ActualSpeed;
}
注意：这里用了最基本的算法实现形式，没有考虑死区问题，没有设定上下限，只是对公式的一种直接的实现，后面的介绍当中还会逐渐的对此改进。
到此为止，PID的基本实现部分就初步完成了。下面是测试代码：
int main(){
printf("System begin \n");
PID_init();
int count=0;
while(count<1000)
{
float speed=PID_realize(200.0);
printf("%f\n",speed);
count++;
}
return 0;
}
增量型PID的C语言实现：
实现过程仍然是分为定义变量、初始化变量、实现控制算法函数、算法测试四个部分，
#include<stdio.h>
#include<stdlib.h>
struct _pid{
float SetSpeed; //定义设定值
float ActualSpeed; //定义实际值
float err; //定义偏差值
float err_next; //定义上一个偏差值
float err_last; //定义最上前的偏差值
float Kp,Ki,Kd; //定义比例、积分、微分系数
}pid;
void PID_init(){
pid.SetSpeed=0.0;
pid.ActualSpeed=0.0;
pid.err=0.0;
pid.err_last=0.0;
pid.err_next=0.0;
pid.Kp=0.2;
pid.Ki=0.015;
pid.Kd=0.2;
}
float PID_realize(float speed){
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
float incrementSpeed=pid.Kp*(pid.err-pid.err_next)+pid.Ki*pid.err+pid.Kd*(pid.err-2*pid.err_next+pid.err_last);//只和前后三次的误差值有关，也方便计算
pid.ActualSpeed+=incrementSpeed;
pid.err_last=pid.err_next;
pid.err_next=pid.err;
return pid.ActualSpeed;
}
int main(){
PID_init();
int count=0;
while(count<1000)
{
float speed=PID_realize(200.0);
printf("%f\n",speed);
count++;
}
return 0;
}
积分分离的PID控制算法C语言实现：
在普通PID控制中，引入积分环节的目的，主要是为了消除静差，提高控制精度。但是在启动、结束或大幅度增减设定时，短时间内系统输出有很大的偏差，会造成PID运算的积分积累，导致控制量超过执行机构可能允许的最大动作范围对应极限控制量，从而引起较大的超调，甚至是震荡，这是绝对不允许的。
为了克服这一问题，引入了积分分离的概念，其基本思路是当被控量与设定值偏差较大时，取消积分作用; 当被控量接近给定值时，引入积分控制，以消除静差，提高精度。其具体实现代码如下：
pid.Kp=0.2;
pid.Ki=0.04;
pid.Kd=0.2; //初始化过程
if(abs(pid.err)>200)
{
index=0;
}else{
index=1;
pid.integral+=pid.err;
}
pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last);
//算法具体实现过程可参考上面的
抗积分饱和的PID控制算法C语言实现：
所谓的积分饱和现象是指如果系统存在一个方向的偏差，PID控制器的输出由于积分作用的不断累加而加大，从而导致执行机构达到极限位置，若控制器输出U(k)继续增大，执行器开度不可能再增大，此时计算机输出控制量超出了正常运行范围而进入饱和区。一旦系统出现反向偏差，u(k)逐渐从饱和区退出。进入饱和区越深则退出饱和区时间越长。在这段时间里，执行机构仍然停留在极限位置而不随偏差反向而立即做出相应的改变，这时系统就像失控一样，造成控制性能恶化，这种现象称为积分饱和现象或积分失控现象。
防止积分饱和的方法之一就是抗积分饱和法，该方法的思路是在计算u(k)时，首先判断上一时刻的控制量u(k-1)是否已经超出了极限范围： 如果u(k-1)>umax，则只累加负偏差; 如果u(k-1)<umin，则只累加正偏差。从而避免控制量长时间停留在饱和区。直接贴出代码，不懂的看看前面几节的介绍。
float PID_realize(float speed){
int index;
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
if(pid.ActualSpeed>pid.umax) //灰色底色表示抗积分饱和的实现
{
if(abs(pid.err)>200) //蓝色标注为积分分离过程
{
index=0;
}else{
index=1;
if(pid.err<0)
{//如果超上限要嘛加负值要嘛就不加了，免得进入饱和区
pid.integral+=pid.err;
}
}
}else if(pid.ActualSpeed<pid.umin){
if(abs(pid.err)>200) //积分分离过程
{
index=0;
}else{
index=1;
if(pid.err>0)
{//如果超下限要嘛加正值要嘛就不加了免得进入饱和区
pid.integral+=pid.err;
}
}
}else{
if(abs(pid.err)>200) //积分分离过程
{
index=0;
}else{
index=1;
pid.integral+=pid.err;
}
}
pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last);
pid.err_last=pid.err;
pid.ActualSpeed=pid.voltage*1.0;
return pid.ActualSpeed;
}
变积分的PID控制算法C语言实现：
变积分PID可以看成是积分分离的PID算法的更一般的形式。在普通的PID控制算法中，由于积分系数ki是常数，所以在整个控制过程中，积分增量是不变的。但是，系统对于积分项的要求是，系统偏差大时，积分作用应该减弱甚至是全无，而在偏差小时，则应该加强。积分系数取大了会产生超调，甚至积分饱和，取小了又不能短时间内消除静差。因此，根据系统的偏差大小改变积分速度是有必要的。
变积分PID的基本思想是设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢; 偏差越小，积分越快。
这里给积分系数前加上一个比例值index：
当abs(err)<180时，index=1;
当180<abs(err)<200时，index=（200-abs(err)）/20;
当abs(err)>200时，index=0;
最终的比例环节的比例系数值为ki*index;
float PID_realize(float speed){
float index;
pid.SetSpeed=speed;
pid.err=pid.SetSpeed-pid.ActualSpeed;
if(abs(pid.err)>200) //变积分过程
{
index=0.0;
}else if(abs(pid.err)<180){
index=1.0;
pid.integral+=pid.err;
}else{
index=(200-abs(pid.err))/20;
pid.integral+=pid.err;
}
pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last);
pid.err_last=pid.err;
pid.ActualSpeed=pid.voltage*1.0;
return pid.ActualSpeed;
}
常用的四轴飞行器PID算法
四轴飞行器常用PID组合：
1.三角函数直接解算欧拉角+互补滤波+单级PID版本
效果：简单暴力，但是补滤波效果差，单级PID响应慢，打舵跟随效应差。
2.三角函数直接解算欧拉角+卡尔曼滤波+单级PID版本
效果：卡尔曼滤波噪声偏大，滞后略微严重，单级PID难操作，打舵响应慢，跟随效应差。不过比较适合初学四轴的人，难度比四元数加串级PID版本低，易于理解。
3.四元数姿态解算+互补滤波（德国开源四轴）+串级PID版本
效果：四元数难理解，基于PI控制的互补滤波不适合非专业人员，PID参数较单级PID参数难调。打舵响应极佳，稳定程度高，易于操作，是目前四轴的主流算法
常用PID：
三角函数直接解算：
加速度计输出的数值为多少个g，就是多少倍加速度，在物体在静止时会受到1个g的重力加速度，如果加速度计水平放置，那么Z轴数据就是1，XY轴就是0，原理不懂的话不用看了，好好读完高中再来研究四轴。当加速度计XY轴产生偏转时，XYZ轴的数值会产生变动，此时根据反三角函数即可解算出当前的角度。
公式：
AngleAx=atan(Angle_ax/sqrt(Angle_ay*Angle_ay+Angle_az*Angle_az))*57.2957795f;
AngleAy=atan(Angle_ay/sqrt(Angle_ax*Angle_ax+Angle_az*Angle_az))*57.2957795f;
后面的数值是180/PI 目的是弧度转角度
这种方法简单实用但是不是太准确，因为不光重力能产生加速度，运动也能产生加速度，当运动产生的加速度引入时，就会干扰解算精度，因此对运动的还原性较差。
此外，网上的版本多是用反正弦函数解算的，那样其实是错的，假使我要解算物体在XZ坐标轴所构成的平面的角度时朝Y轴偏移了一点，那么解算出来的值就是错的，原因自己画图想想吧。
互补滤波：
当我们用三角函数直接解算出姿态后，需要对其经行滤波以及和陀螺仪的数据进行融合。因为加速度是很容易受外界干扰的，一个手机开了震动模式放在水平面上，实际角度是0度，但是解算出来的值是在0度正负某个范围内呈均匀分布的，这样的值显然不适合使用，因此需要陀螺仪的帮组。陀螺仪输出的数据是多少度一秒，对这个数据积分就可以算出系统偏转过的角度。陀螺仪受震动影响小，故短时间内可以信任它，但是陀螺仪会有温飘，其误差是随着温度而改变的，陀螺仪出厂后还会存在一定的静差，而且积分也有误差，故长时间不能信任陀螺仪。由于加速度计长时间来说值得信任，故可以用互补滤波来融合二者的优点，消减二者的缺点。
公式：Angle=0.95*(Angle-Angle_gy*dt)+0.05*AngleAx; 陀螺仪数据正负号根据自己需要而改变
在上式中我们可以看出互补滤波是由两个小式子相加得到的，小式子前有一个系数，二者相加为1，我们可以理解这两个数是我们对加速度计和陀螺仪的信任度，你信任哪个的程度大点，哪个的权值就相应的变大，其输出数据在最终结果中占的比重也越大。前面一个式子是用陀螺仪积分计算角度，后面一个式子是用加速度计解算出的角度，当加速度计比重很小时就可以压制加速度噪声，也就是进行了低通滤波，前式也就是对陀螺仪进行了高通滤波。从公式中不难得出互补滤波的原理，陀螺仪占的比重偏大，短时间内以陀螺仪数据为准，加速度计占的比重较小，长时间内以加速度计来校准角度数据。
一般情况下来讲，陀螺仪比加速度计的比值取值为0.95：0.05或0.98：0.02。当然也可以根据实际情况降低陀螺仪的比重。
单极PID：
当你知道系统当前状态和期望状态后，如何将系统从当前状态调整到期望状态是个问题，在此我们可以用PID进行调整，PID分为位置式和增量式，位置式适合舵机等系统，在此使用的是增量式。
公式：PID=P*e(n)+I*[(e(n)+e(n-1)+…+e(0)]+D*[e(n)-e(n-1)]
D后面的当前误差减前次误差也可以直接使用陀螺仪的数据代替，原理一样。
单级PID整定方法参见我写的第一篇帖子！
串级PID：
单极PID适合线性系统，当输出量和被控制量呈线性关系时单极PID能获得较好的效果，但是四轴不是线性系统，现代学者认为，四轴通常可以简化为一个二阶阻尼系统。为什么四轴不是线性系统呢？首先，输出的电压和电机转速不是呈正比的，其次，螺旋桨转速和升力是平方倍关系，故单极PID在四轴上很难取得很好效果，能飞，但是不好飞。
为了解决这个问题，我们提出了串级PID这个解决方法。
串级PID就是两个PID串在一起，分为内环和外环PID。在此，我们使用内环PID控制，外环PI控制。
单极PID输入的是期望角度，反馈的是角度数据，串级PID中外环输入反馈的也是角度数据，内环输入反馈的便是角速度数据。通俗来讲，内环就是你希望将四轴以多少度每秒的速度运动，然后他给你纠正过来，外环就是根据角度偏差告诉内环你该以多少度一秒运动。这样，即使外环数据剧烈变化，四轴的效果也不会显得很僵硬。
在内环中，PID三个数据作用分别是：P（将四轴从偏差角速度纠正回期望角速度）D（抑制系统运动）I（消除角速度控制静差）
外环PI中，两个数据的作用是：P（将四轴从偏差角度纠正回期望角度）I（消除角度控制静差）
refer：
https://blog.csdn.net/gen_ye/article/details/52534609
http://bbs.elecfans.com/jishu_1615869_1_1.html
https://blog.csdn.net/mish84/article/details/51062165
更多阅读：
位置式PID与增量式PID的区别：http://www.elecfans.com/dianzichangshi/20171124585738.html
卡尔曼滤波的原理说明，附源代码 ：http://bbs.elecfans.com/jishu_484128_1_1.html
【开源】分享一个经典的串级PID算法，附源代码 ：http://bbs.elecfans.com/jishu_486485_1_1.html
教你在单片机上套公式实现卡尔曼滤波器 ；http://bbs.elecfans.com/jishu_484132_1_1.html
四元数互补滤波(目前匿名等四轴也是用这个解算方)：http://bbs.elecfans.com/jishu_4757431_1.html
