查找
0.PTA得分截图

1.本周学习总结
1.1总结查找内容
查找算法的评价指标——ASL
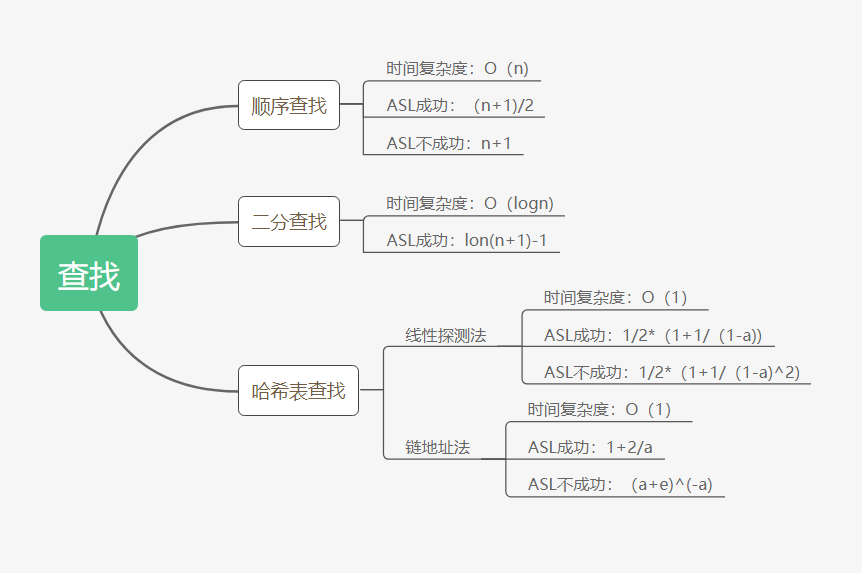
ASL,关键字平均比较的次数,也称平均搜索长度.
ASL(成功):指找到集合T中任一记录平均需要的关键字比较次数
顺序查找:

int SeqSearch(int *a,int n,int k)
{
int i=0;
while(i<n&&a[i]!=k)
{
i++;
}
if(i>=n) //没找到,返回-1
{
return -1;
}
else
{
return i;
}
}
- 时间复杂度:O(n)
- 查找成功时的平均比较次数约为表长一半
- 查找不成功时的平均查找长度为:n
二分查找
二分查找也叫折半查找,要求线性表中的元素必须从小到大排列或者从大到小排列
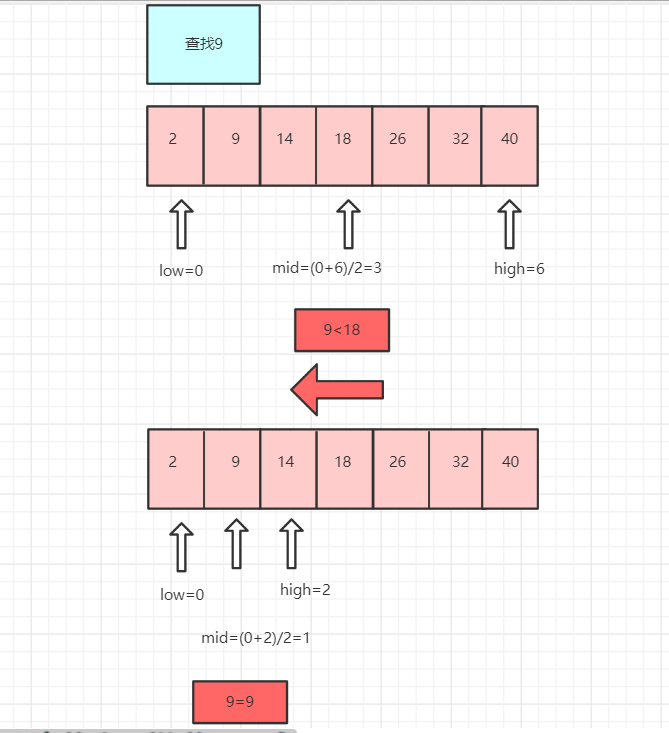
int BinSearch(int *a,int n,int k)
{
int low=0,high=n-1,mid;
while(low<=high)
{
mid=(mid+high)/2;
if(a[mid]==k)
{
return mid+1;
}
if(k<a[mid])
{
high=mid-1;
}
else
{
low=mid+1;
}
}
return -1; //没找到
}
//递归代码
int BinSearch(int *a,int low,int high,int k)
{
int mid;
if(low<high)
{
mid=(low+high)/2;
if(a[mid]==k)
return mid+1;
if(a[mid]>k)
BinSearch(a, low,mid-1, k) ;
else
BinSearch(a, low,mid+1, k) ;
}
else
return -1;
}
//时间复杂度:T(n)=T(n/2)+1
- 时间复杂度:其实这样的过程,while循环查找的方法就很像建立了一个二叉搜索树,最后搜索的是一条路径,所以时间复杂度是O(logn)
- ASL=log(n+1)-1
计算二分查找,二叉排序树的ASL
给出如下例子
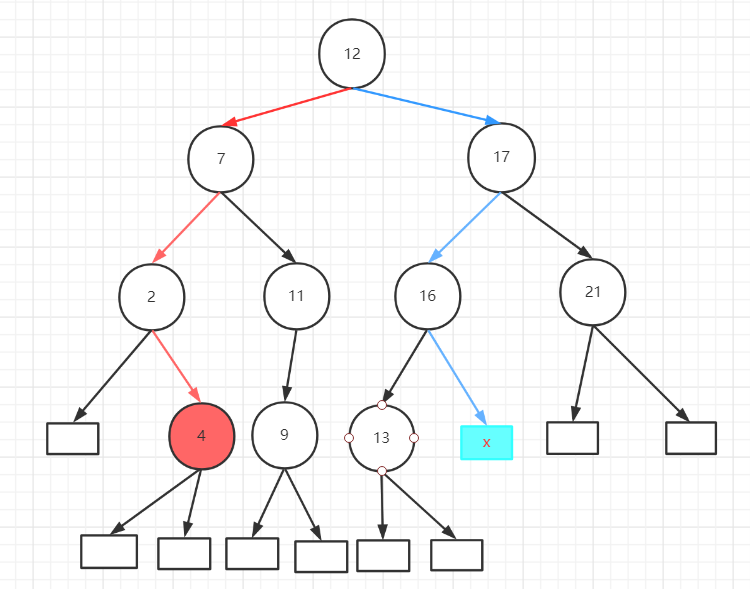
ASL(成功):(各个关键字比较的次数/有效节点)
1 * 1+2 * 2+3 *4 +4 * 3)/10=2.9
ASL(不成功):(各个空节点比较的次数/(总节点数+所有空节点)),不成功,说明肯定都找到叶子节点里去了,因此总节点数就是有效节点+空节点
(3 * 5+4 * 6)/11=3.54
二叉搜索(排序)树
特点:
若左子树不空,则右子树所有节点的值均小于根节点的值
若右子树不空,则右子树所有节点的值均大于根节点的值
左右子树也都是二叉排序树
ps:
二叉排序中,没有相同关键字的节点
中序遍历二叉搜索树,会发现得到的序列是递增的
二叉排序树结构体定义
typedef struct node
{
int key;
InfoType data;//其它数据域
struct node *lchild,*rchild;//左右孩子指针
}BSTNode,*BSTree;
建二叉排序树
int InsertBST(BSTree &p,int k)
{
if(p==NULL)//插入永远都在叶子节点插入
{
p=new BSTNode;
p->key=k;
p->lchild=p->rchild=NULL;
return 1;
}
else if(k==p->key)
{
return 0;
}
else if(k<p->key)
{
return InsertBST(p->lchild,k);
}
else
{
return InsertBST(p->rchild,k);
}
}
查找关键字
BSTNode *SearchBST(BSTNode *bt,int k)
{
if(bt==NULL||bt->key==k)
{
return bt;
}
if(k<bt->key)
{
return SearchBST(bt->lchild, k);
}
else
{
return SearchBST(bt->rchild, k);
}
}
//非递归查找
BSTNode *SearchBST1(BSTNode *bt,int k)
{
while(bt!=NULL)
{
if(k--bt->key)
{
return bt;
}
else if(k<bt->key)
{
bt=bt->lchild;
}
else
bt=bt->rchild;
}
return NULL;
}
查找最大/最小关键字节点
int maxnode(BSTNode *p)
{
while (p->rchild!=NULL)//最大值一定在最右不为空的叶子节点
p=p->rchild;
return(p->data);
}
int minnode(BSTNode *p)
{
while (p->lchild!=NULL)//最小值一定在最左不为空的叶子节点
p=p->lchild;
return(p->data);
}
二叉排序树删除叶子节点
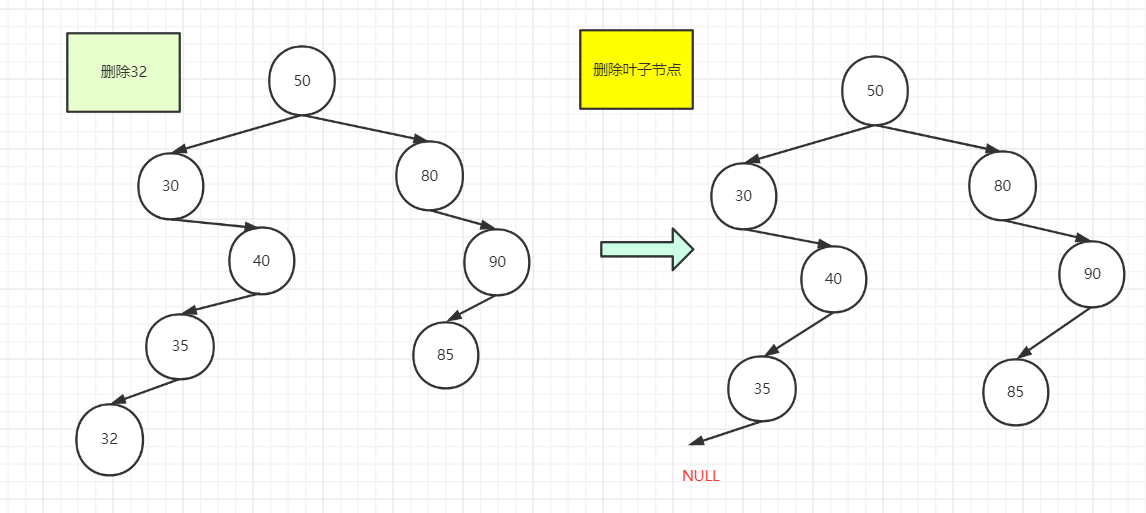
直接将双亲节点指向叶子节点的指针域指向空,接着删除叶子节点
二叉排序树删除的节点只有左子树或右子树
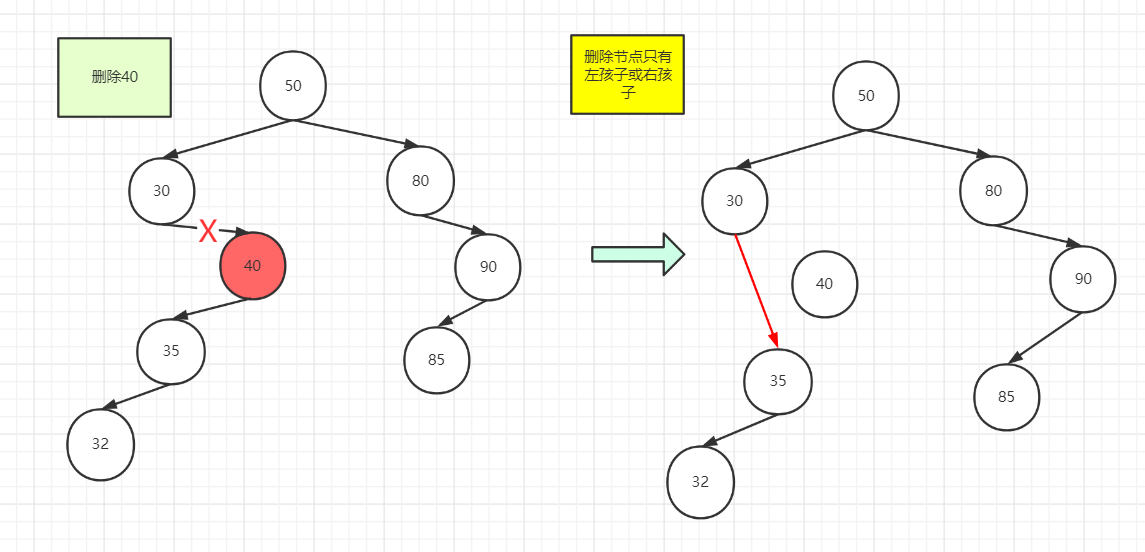
对于删除只有左孩子或右孩子的节点,只要让双亲节点的指针域指向它的左孩子或右孩子,对于上面这个图,对于30一个节点,删除它的右孩子40,那么无论是40的左孩子还是右孩子,都会比30大,因为我们要保持二叉搜索树的特点,所以直接把30这个节点的指针域指向40这个节点的左孩子或右孩子即可
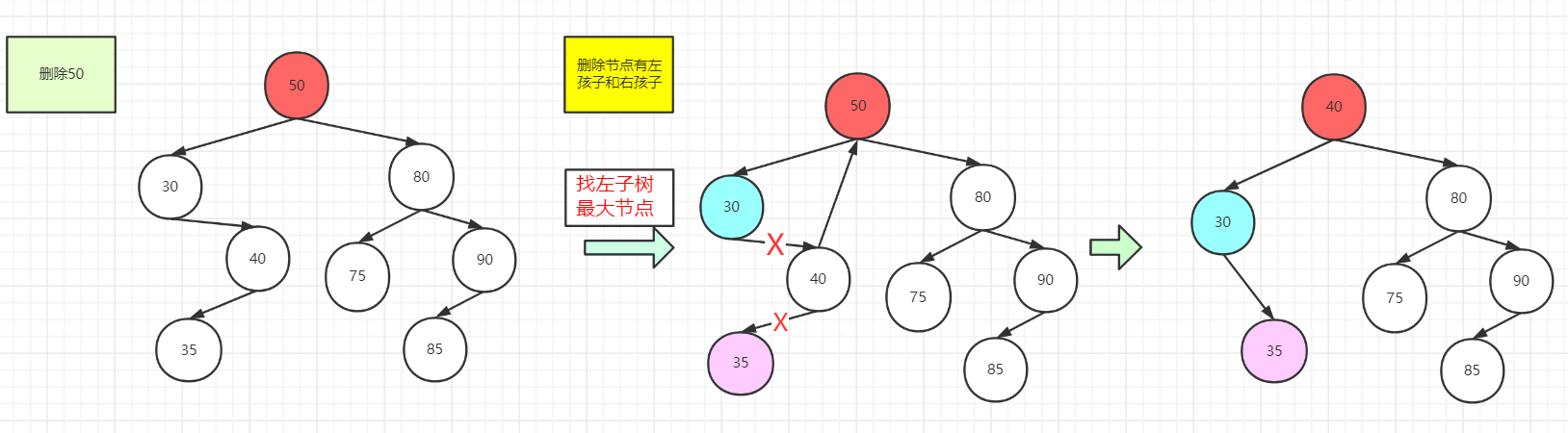
二叉排序树删除的节点既有左子树和右子树
这是删除节点中最麻烦的一个,但是我们只要始终记住二叉树左右孩子,和根节点的关系即可
删除节点,有两种办法
1.以前驱代替之,再删除该节点,前驱就是左子树中最大的节点
2.以后继代替之,再删除该节点,后继就是右子树中最小的节点
为什么这么选,就是因为要保持二叉搜索树的特性,左子树<根节点<右子树
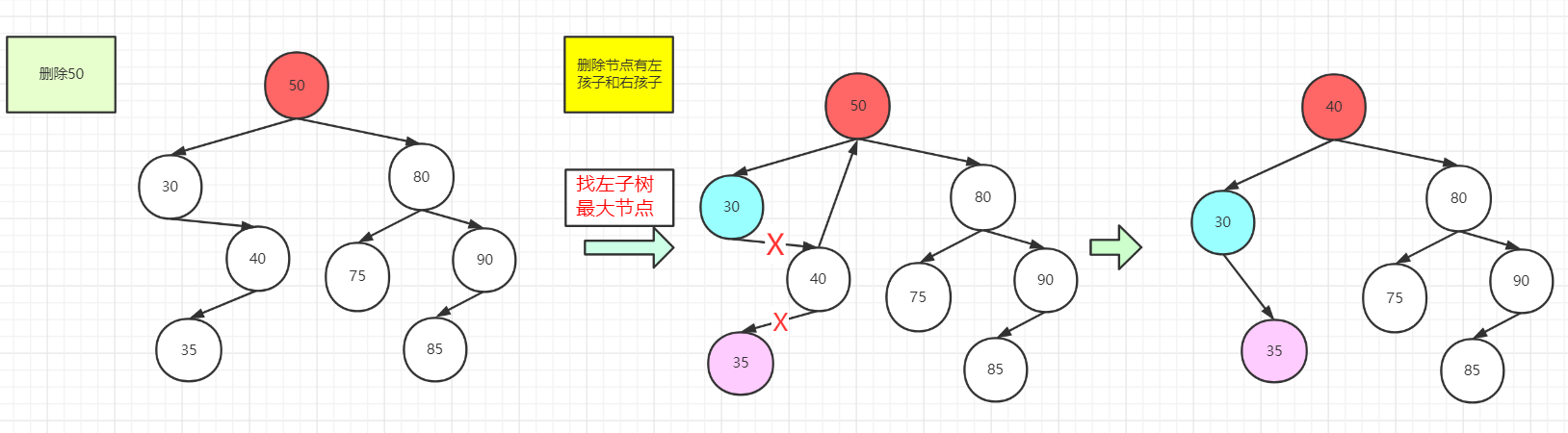
找到50,选择左子树最大节点进行代替,用图画出来其实可以很明了,直接看他左子树30,40,35,最大的就是40,直接代替50,接着我们就要安排接下来35这个节点,其实一开始学的,我很懵,因为对于剩下节点我不知道怎么安排,后来,学着学着,就有感觉来,35不是比30大嘛,就直接放它的右子树好了
对于这个图,我画的有点不好,因为对于从50到80这个指针域并没有断掉,因为删除节点,是把50这个节点的数据域改了一下,我们找到50,然后找到右子树的最小节点,80,75,90,85,最小,就是75,把50的值改为75,接着,由于75下面也没啥节点了,就不处理了,如果有的话,记住特性安排,就好了。
int DeleteBST(BSTree &bt,KeyType k) //查找要删除的节点
{ if (bt==NULL) return 0; //空树删除失败
else if(k<bt->key)
{
return DeleteBST(bt->lchild,k);
//递归在左子树中删除为k的节点
}
else if(k>bt->key)
{
return DeleteBST(bt->rchild,k);
//递归在右子树中删除为k的节点
}
else
{ Delete(bt); //删除*bt节点
return 1;
}
}
}
void Delete(BSTreee &p) //从二叉排序树中删除*p节点
{ BSTNode *q;
if (p->rchild==NULL) //*p节点没有右子树的情况
{
q=p;
p=p->lchild;
delete q;
}
else if (p->lchild==NULL) //*p节点没有左子树
{
q=p;
p=p->rchild;
delete q;
}
else Delete1(p,p->lchild);
//*p节点既有左子树又有右子树的情况
//找到左子树最大的节点,一定是左孩子的最右孩子节点
}
void Delete1(BSTNode *p,BSTNode *&r) //被删节点:p,p的左子树节点:r
{ BSTNode *q;
if (r->rchild!=NULL)//递归找最右下节点
Delete1(p,r->rchild)
else //找到了最右下节点*r
{
//将*r的关键字值赋给*p
p->key=r->key;
q=r;
r=r->lchild;
delete q;
}
}
平衡二叉树(AVL树)
引入原因:为了解决二叉搜索树极端的情况,如单支树,那时,查找的ASL,就好顺序查找一样
特点:
1.左右子树是平衡二叉树
2.所有节点的左右子树深度(高度)之差的绝对值<=1,在平衡二叉树里,用平衡因子来表示左右子树的高度之差,从而控制树的平衡
由于有平衡因子的参与,所以不会存在最坏,最极端的情况,所以时间复杂度是O(logn)
AVL四种调节
对于AVL四种调节,我们要做的,也就只有一点,就是保证它是二叉搜索树。
LL平衡旋转
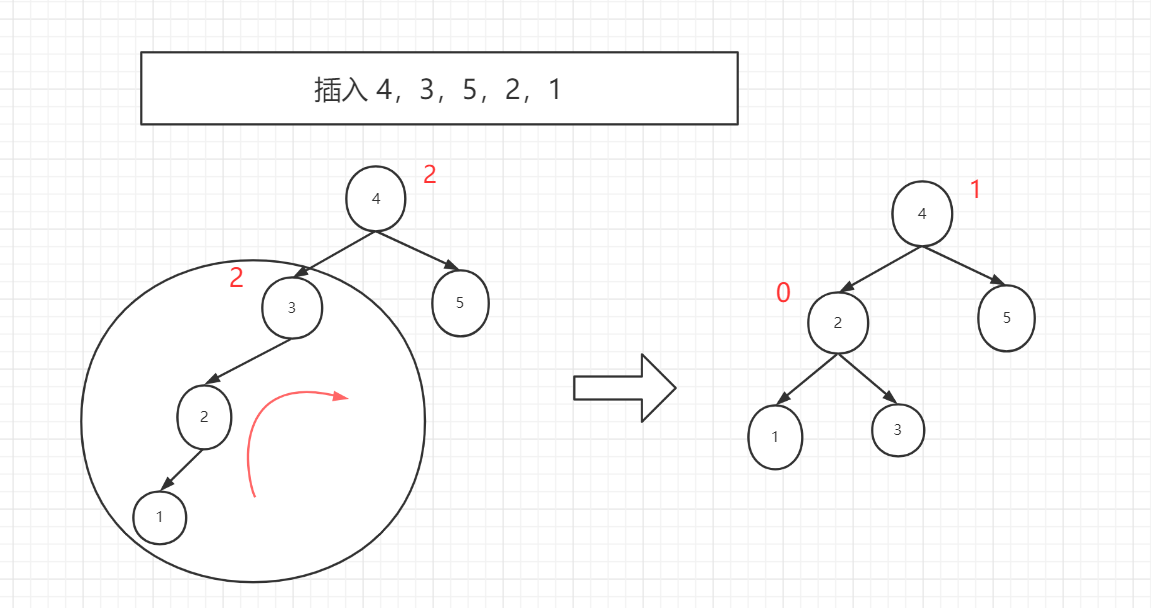
对于一棵树中,发现有两个失衡点,3和4,我们要从底部往上调节,第一个失衡点3,然后它的旋转点就是2,让2进行旋转,往往我们从下面开始,第二个失衡点也会平衡,不在失衡
RR平衡调节
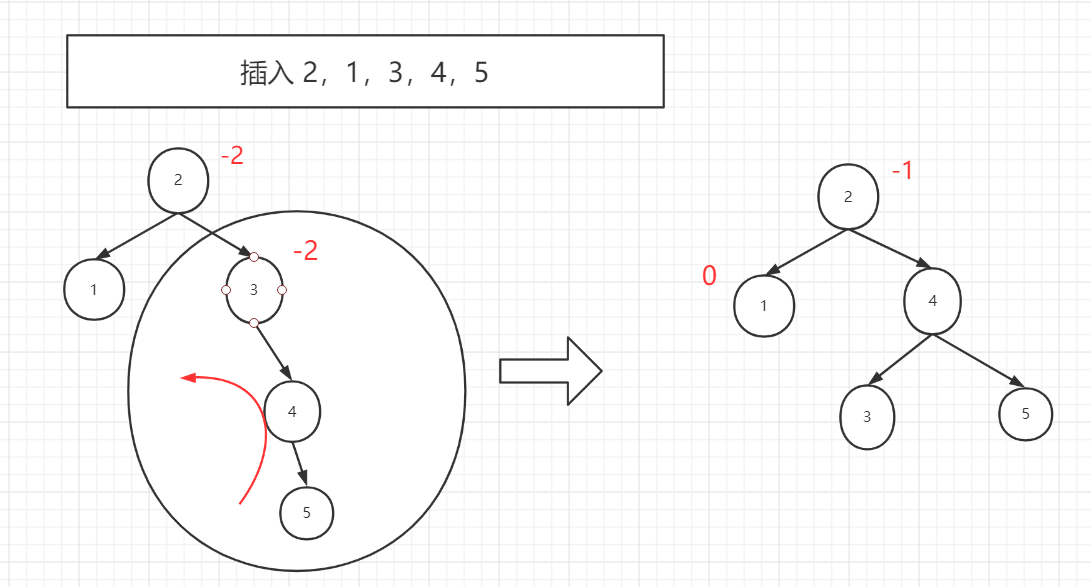
这个调整和LL调整一样,我们要做的是找到失衡点和旋转点,怎么旋转,也是要看二叉搜索树的特点,左子树<根节点<右子树
RL调整
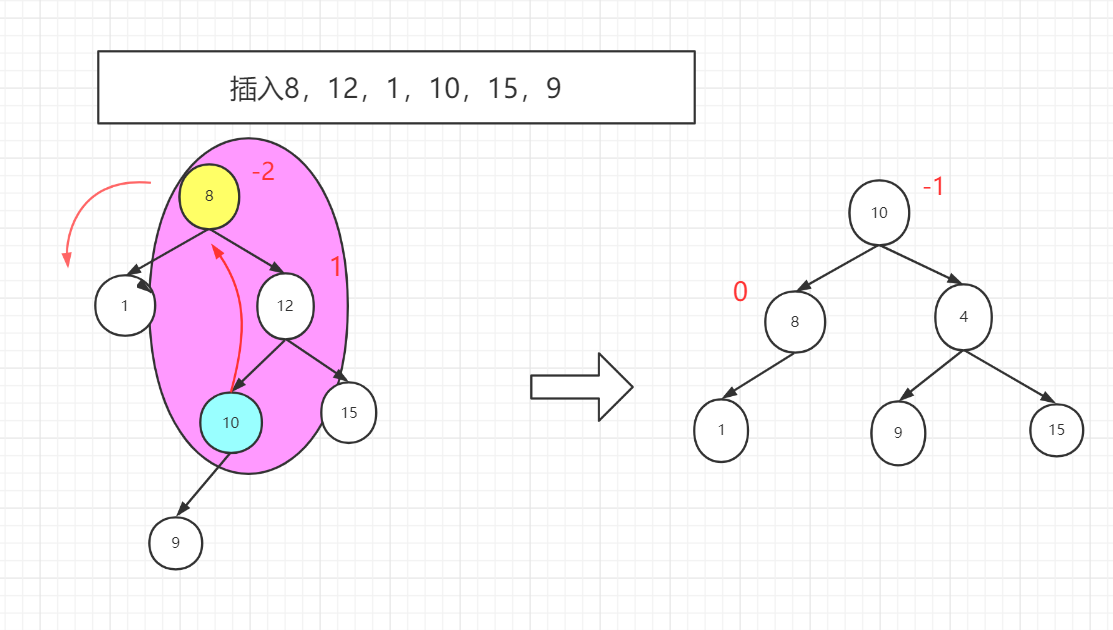
插入9之后,发现8的平衡因子变为-2,所以失衡点是-2,开始寻找旋转点,9是在8的右子树的左孩子是,所以是RL调整,旋转点是10,10代替8的位置,8往左下旋转,那么本来是10的孩子9,就要按照AVL树的特点,被安排为12的左孩子。
LR调整也是和上面一样的。
节点个数n最少的平衡二叉树
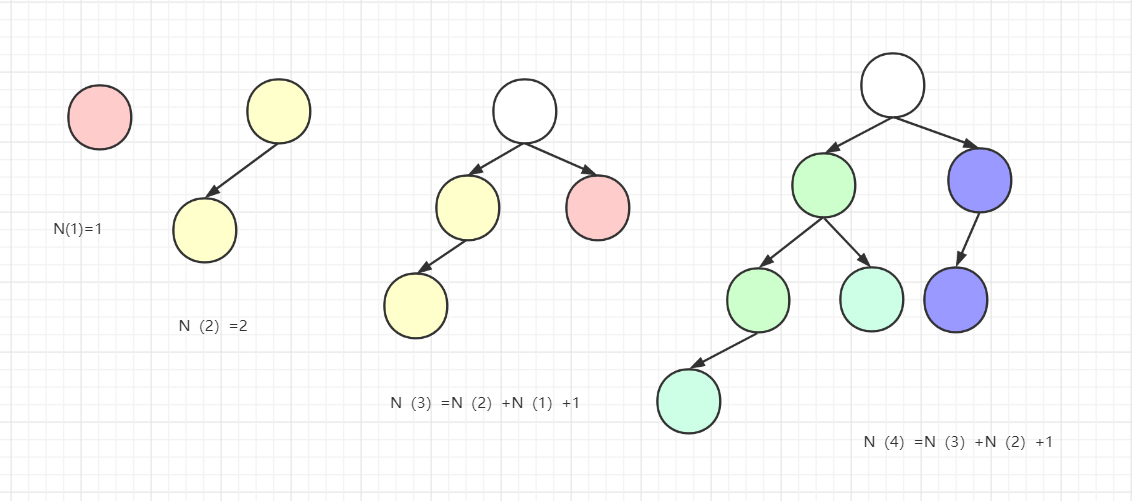
-
高度为h的平衡二叉树,节点个数为N(h)=N(h-1)+N(h-2)+1
-
平衡二叉树高度h和n的关系:h=log(n+1)
-
平衡二叉树上最好 最坏进行查找关键字的比较次数不会超过平衡二叉树的深度O(logn)
B(-)树,B+树
引用原因:BST,AVL都只适合小数据量,每个节点放一个关键字,当数据量大时,树的高度也会很大
B树和B+树:一个节点可以放多个关键字,降低树的高度,适合大数据量查找,如数据库中的数据
B-树,又叫做多路平衡查找树
一棵m阶B-树
特点:
1.每个节点最多m个孩子,意味着关键字最多有m-1个
2.除了根节点至少有两个孩子节点,其它节点都至少有m/2(上界)个孩子,说明节点最少有m/2(上界))-1个关键字。
3.B-树是所有节点的平衡因子均等于0的多路查找树,叶子节点必须在同一层
B-树的结构体定义
#define MAXN 10
typedef int KeyTypw;
typedef struct node
{
int keynum;//节点当前拥有关键字的个数
KeyType key[MAXM];//存放关键字
struct node *parent;//双亲节点指针
struct node *ptr[MAXM];//孩子节点指针数组
}BTNode;
B-树的插入
- 向B-树中插入关键字,可能引起节点的分裂,最终可能导致整个B-树的高度增一
- 插入的节点一定是叶子节点层
插入关键字后,节点关键字个数<m-1(m表示阶数)
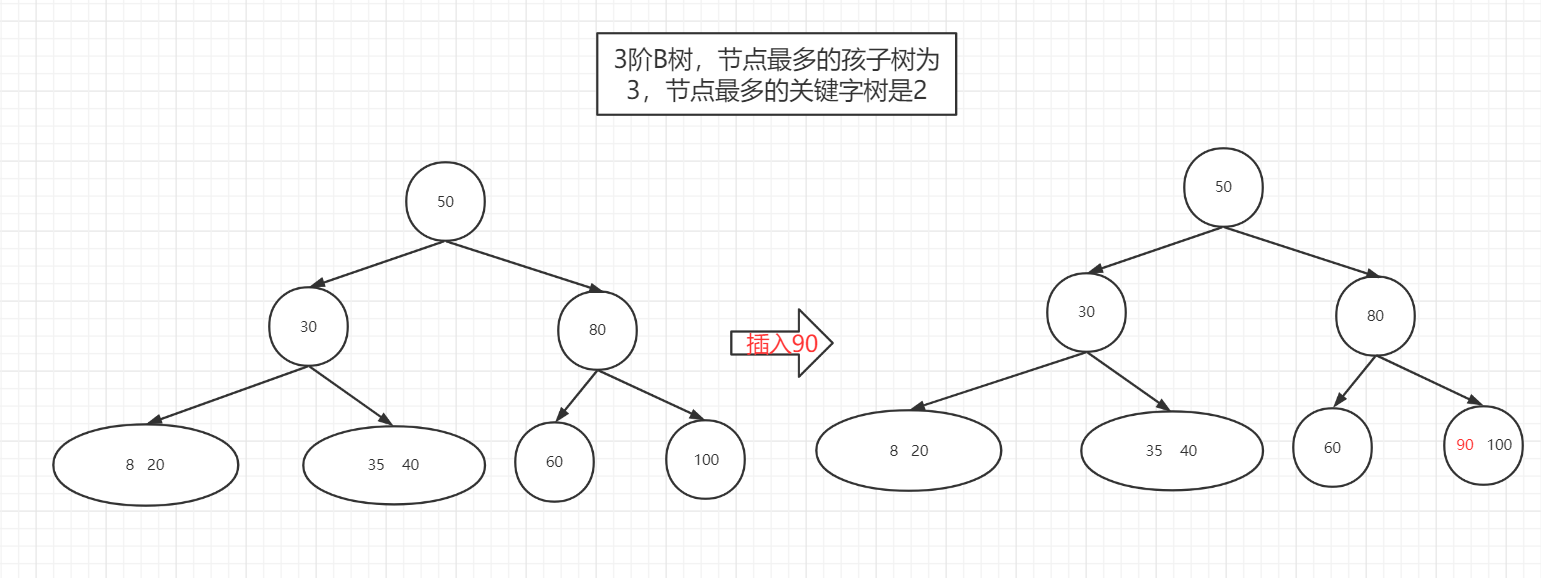
如果节点关键字个数<m-1,直接插入叶子节点即可,要注意,在节点里,插入的关键字要按顺序排列
插入关键字后,节点关键字个数=m,此时需要进行分裂

由于叶子节点插入一个新的关键字,导致节点过饱和,所以我们要把多出来的一个节点给父亲节点,而多出来的节点是按照序列排序,最中间的节点,不是最大的,也不是最小的,给了父亲节点之后,发现父亲节点可以表示的范围区间多了一个,那接下来,就是按照区间把剩下的关键字进行排序即可。
B-树的删除(m表示阶数)
- 在B-树中删除关键字,可能引起节点的合并,最终可能导致整个B-树的高度减一
未删除时节点中关键字个数>m/2(上界)-1,直接删除
删除叶子节点
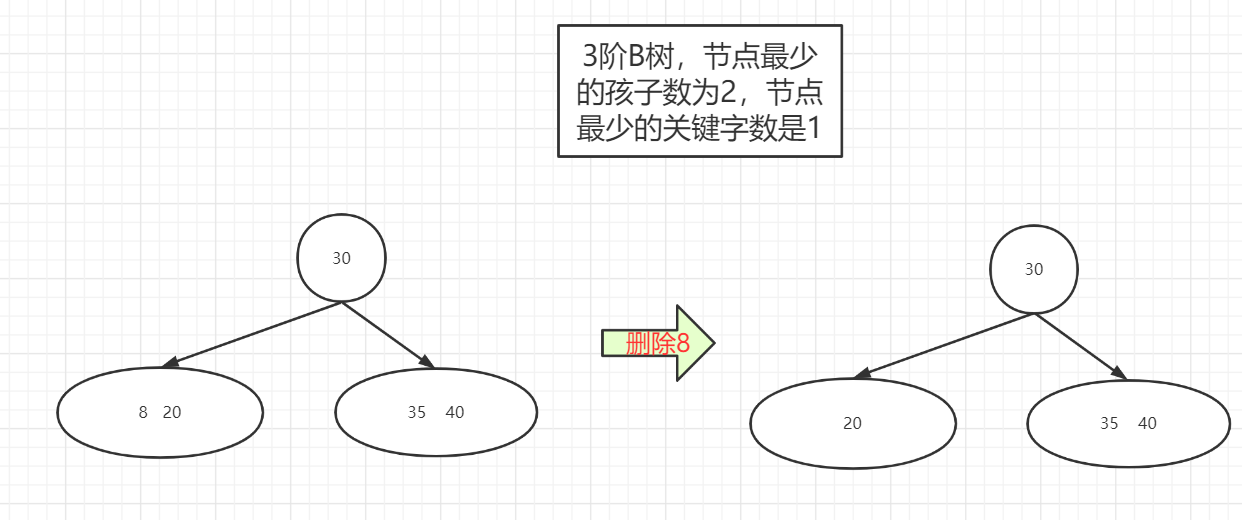
删除非叶子节点
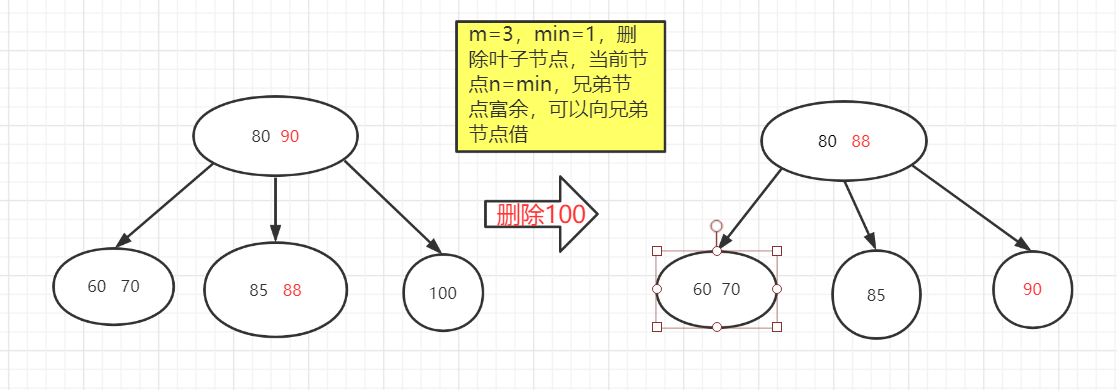
节点中关键字个数=m/2(上界)-1
删除叶子节点:
1.如果兄弟富余(节点个数>min),向兄弟借
节点方式是把兄弟节点的最小值或最大值(看情况)给父亲节点,把父亲节点的最大值或最小值给自己,这样以后,才能继续保持b树的特点
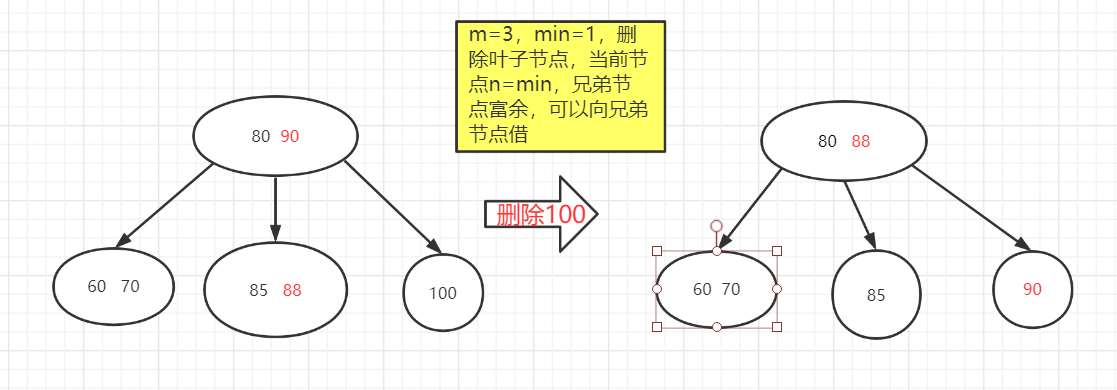
2.如果兄弟节点的关键字数也等于min,没有富余,那么只好进行合并
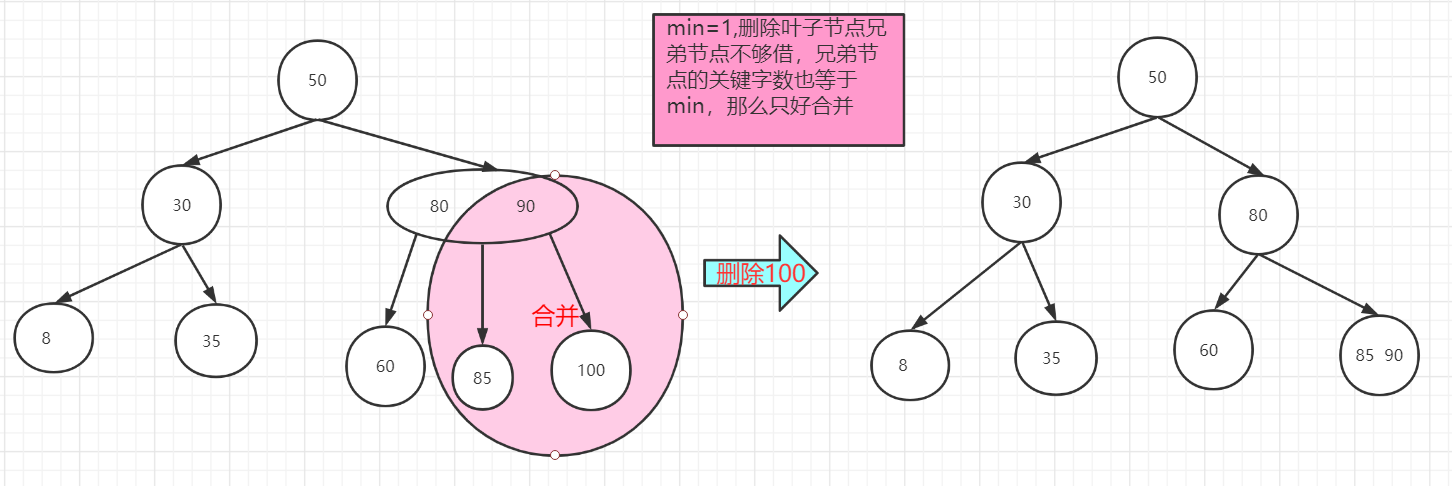
删除非叶子节点
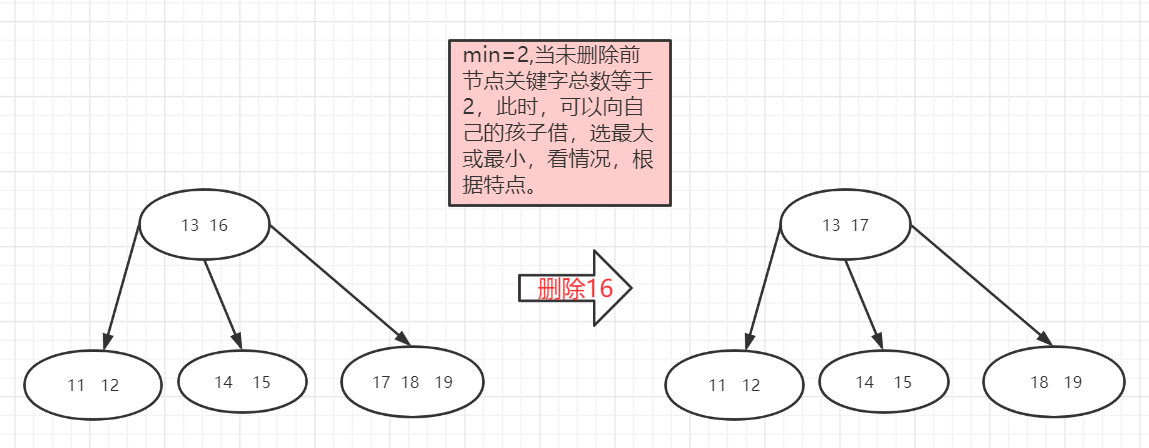
如果孩子富余,向孩子节点借,从中选择最大或最小的值,要看情况选择
B树的应用
B树常被用于对检索时间要求苛刻的场合
1.B-树索引是数据库中存取和查找文件的方法
2.硬盘中的节点也是B-树结构,B-树利用多个分支(称为子树)的节点,减少获取记录时所经历的节点数,从而达到节省存取时间的目的
B+树
B+树是大型索引文件的标准组织方式
特点:
1.每个分支节点至少有m棵子树
2.根节点或者没有子树,或者至少有两颗子树
3.除根节点,其它每个分支节点至少有m/2(上界)棵子树
4.有n棵子树的节点有n个关键字
5.所有叶子节点包含全部关键字及指向相应记录的指针
6.所有分支节点只是起到索引的作用。
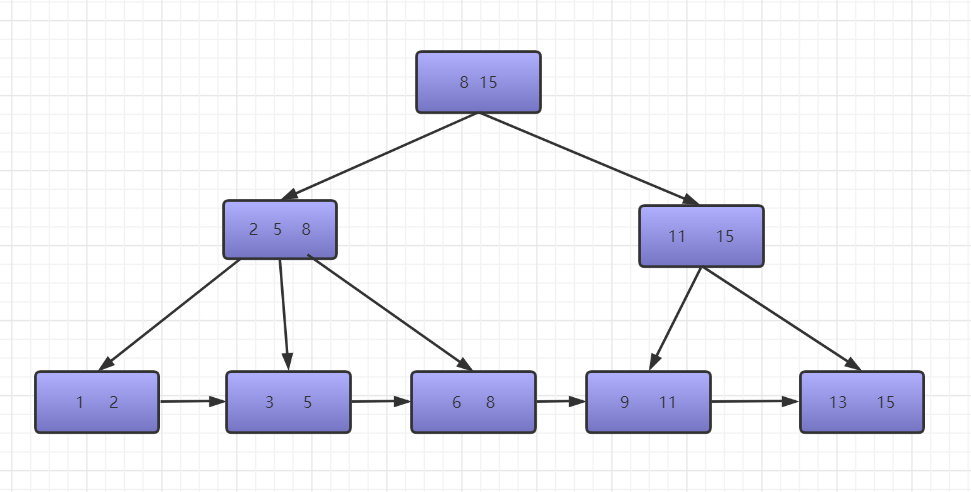
ps:
1.每一个叶子节点都有一个指针,指向下一个数据,形成一个有序链表
2.只有叶子节点才有data,其它都是索引
B+树和B树的区别
1.有k个子节点的节点必然有k个关键字
2.非叶子节点仅具有索引作用,跟记录有关的信息均存放在叶子节点中
3.树的所有叶节点构成一个有序链表,可以按照关键字的次序遍历全部记录
B+树的优点
1.B树查找并不稳定(最好的情况是查询根节点,最坏的情况是查询叶子节点),而B+树的每次查找都是稳定的。
2.由于B+树中间节点没有data数据,所以相同大小的磁盘页可以容纳更多的节点元素,所以数据量相同的情况下,B+树比B树更矮胖,查询次数更少
所以,比起B树,B+树查询性能很稳定,查询范围更广
散列查找
哈希表
哈希表是一种线性存储结构,记录关键字与存储地址存在某种函数关系的结构
装填因子=存储的记录个数/哈希表的大小,哈希表长度和装填因子有关,装填因子越小,冲突可能性就越小
哈希表的构造方法
直接定址法
哈希函数:h(k)=k+c
优点:
函数计算简单,并且不会存在哈徐冲突的情况
缺点:
1.当大数据可能分布不是那么集中时,直接定址法会造成空间的大量浪费
除留余数法
除留余数法是用关键字k除以某个不大于哈希表长度m的数p(最好是素数——所得的余数作为哈希地址的方法。
哈希函数:h(k)=k mod p
例题:
将关键字序列{7,8,30,11,18,9,14}散列存储到散列表中,散列表的存储空间是一个下标从0开始的一维数组,散列函数为:H(key)=(key×3) mod 7,要求装填(载)因子为0.7。画出所构造的散列表。
解题步骤:
第一步:算出表长:m=p/装填因子,p是模,即7.所以m=10.
第二部,按照哈希函数的关系,进行计算,并填表。
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 7,14 | 8 | 11,18 | 30,9 |
通过上面,在一些条件下,我们就可以发现,很容易引起冲突,于是我们进行改进
线性探测法解决冲突
d0=h(k); //要着重注意,这里面mod p ,p与m没有任何关系
di=(di-1 + 1)mod m;
m指的是表长
当每次一发现冲突的时候,就继续顺着哈希表往下+1进行探索,直到不发生冲突
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 7 | 14 | 8 | 11 | 30 | 18 | 9 | |||
| 探测次数 | 1 | 2 | 1 | 1 | 1 | 3 | 3 |
算探测次数:
首先,计算表长m=10,这个很重要,因为接下来是%m,不能弄错,
在计算探测次数的时候,是%表长,而计算不成功ASL时,是/p,而p是题目给的,跟表长没关系
14
d0=14*3%7=0,位置上已经有7了,移到下一个,第一次算,是按哈数函数算,mod7
d1=(0+1)%10=3,发现位置,入座,第二次算,以及接下来,都是mod表长
cnt=2;
18
d0=18*3%7=5,有人了
d1=(5+1)%10=6,有人了
d2=(6+1)%10=7,没人,可以坐了
探测平方法解决冲突
d0=h(k)
di(d0 +(-) i^2)mod m
查找的位置依次为d0, d0+1, d0-1,d0+4,d0-4,,,,,,,
特点:
可以避免出现堆积现象,它的缺点是不能糖茶到哈希表上的所有单元,但至少能探查一半
依旧是上面的题目
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 7 | 14 | 8 | 18 | 11 | 30 | 9 | |||
| 探测次数 | 1 | 2 | 1 | 3 | 1 | 1 | 2 |
首先,也是要计算m等于表长=10(根据装填因子)
18
d0=18*3%7=5 有11
d1=(5+1)%10=6 有30
d2=(5-1)%10=4 没人,可以坐
cnt=3
9
d0=9*3%7=6 有30
d1=(6+1)%10=7 没人
线性探测法计算ASL
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 关键字 | 7 | 14 | 8 | 11 | 30 | 18 | 9 | |||
| 成功探测次数 | 1 | 2 | 1 | 1 | 1 | 3 | 3 | |||
| 不成功探测次数 | 3 | 2 | 1 | 2 | 1 | 5 | 4 | 3 | 2 | 1 |
ASL(成功)的计算范围是在那些有记录数据的地方,既然要成功,肯定就在他们当中找
ASL(成功)=(有数字的关键字探测总次数)/有数据的关键字总数
ASL=(1+2+1+1+3+3)/7
ps:/的是有数据的关键字总数,而不是表的长度10
ASL(不成功),其实是从每个下标(0开始)查找到没有数据,即空的位置的次数,因为是不成功,所以是%p,肯定是在1~p-1的范围内,即p,所以是/p,而不是/表长
ASL=(3+2+1+2+1+5+4+3+2+1)/7
如从下标0开始,遇到的第一个没有数据的点是下标为2的时候,探测次数为3
从下标1开始,遇到第一个没有数据的点是下标为2的时候,探测次数为2
........
拉链法解决冲突
把具有相同地址的关键字用一条链连在一起
例题:
设一组初始记录关键字集合为(25,10,8,27,32,68),散列表的长度为8,散列函数H(k)=k mod 7,要求:
ASL(成功)是找到有关键字的链节点*比较次数/所有关键字节点的个数
ASL(成功)=(1+1+1+1+1+2)/6
ASL(不成功)是遍历了整个哈希表(左边的数组)和哈希链,也没有找到我们要找到的数据
对于有一个节点的单链表,不成功需要一次的关键词比较,总共有4个这样的单链表
对于有两个节点的链表,不成功需要两次的关键字比较,总共有1个这样的链表
ASL(不成功)=(4 * 1+1 * 2)/7
总结:
线性探测法算探测次数的时候,第一次是mod p,即按公式,接下来,是mod 表长,如果题目没给,要根据装填因子算
算ASL成功的时候,是/关键字的个数
算ASL不成功的时候,是/p,p是多少就是多少,和表长没关系
哈希表代码实现
哈希表结构体
#define MaxSize 100
#define NULLKEY -1
#define DELKEY -2
typedef char * InfoType ;
typedef struct{
int key; // 关键字域
InfoType data; //其他数据域
int count; //探查次数
}HashTable[MaxSize];
哈希表插入
int InsertHT(HashTable ha,int p,int k,int &n) //建表是边输入边插入的过程,重复调用这个函数
{
int adr,i;
adr=k % p;
if(adr==NULLKEY || adr==DELKEY) //地址为空,可插入数据
{
ha[adr].key=k;
ha[adr].count=1;
}
else
{ i=1;//计算探测次数
while(ha[adr].key!=NULLKEY && ha[adr].key!=DELKEY)
{
adr=(adr+1) % m;
i++;
}//查找插入位置
ha[adr].key=k;
ha[adr].count=i; //找到插入位置
}
n++;
}
哈希表查找
int SearchHT(HashTable ha,int p,int k)
{
int i=0,adr;
adr=k % p;
while(ha[adr].key!=NULLKEY && ha[adr].key!=k)
{
adr=(adr+1) % m;//探查下一个地址
}
if(ha[adr].key==NULLKEY)
return -1;//地址为空,找不到
if(ha[adr].key==k)
return adr; //找到关键字k
else
return -1;
}
哈希表删除
int DeleteHT(HashTable ha,int p,int k,int &n)
{
int adr;
adr=SearchHT(ha,p,k);
if(adr!=-1)
{
ha[adr].key=DELKEY;//逻辑删除,该元素贴删除标记
n--;
return 1;
}
else
return 0;
}
哈希链结构体
typedef struct _Node
{
int data;
struct Node*next;
}HashNode,*HashList;//链节点的结构体定义
哈希链初始化
void Init_hash(HashList hash)
{
int i;
Node *hash=new HashNode[HASHSIZE];
for(i=0; i<HASHSIZE; i++) {
hash[i].next = NULL;//初始化每个槽位
}
}
哈希链搜索
HashList Search_Hash(HashList &hash,int key ,int adr)
{
HashList p;
int i;
p=hash[adr].next;
while(p)
{
if(p->data==key)
{//有重复关键字出现
break;
}
p=p->next;
}
return p;
}
哈希链插入
void Insert_Hash(HashList &hash,int p)
{
int adr,key;
int i;
HashList p;
for(i=0;i<n;i++)
{
cin<<key;
adr=key%p;
p=Search_Hash(hash,key,adr);
if(p==NULL)
{
p=new HashNode;
p->data=key;
p->next=hash[adr].next;
hash[adr].next=p;
}
}
}
1.2谈谈你对查找的认识及学习体会
查找在我们生活中的应用非常广泛,我们的搜索引擎,查找软件的路径,查找聊天记录,因为太过平常,所以可能很少时候,会去想,世界每时每分都有新的信息传到互联网,而我们,只是在小小的搜索框里,就可以搜索到大部分的它们,并且是在我们按下回车的那个瞬间,为什么查找搜索的速度可以如此之快,查找这章,为我开启了一小扇窗户,让我了解了不同数据的存储结构,不同的数据结构,有不一样的应用场合,有不一样的搜索速度,通过树结构演变而来的二叉搜索树,平衡二叉树,b树,b+树,都是为了适应时代的需求,我们该感叹那些前人的智慧,我到现在都在为计算机里小小的二进制数字可以转变成多种多样的形式而感到神奇,向前人的智慧致敬。
2. PTA题目介绍
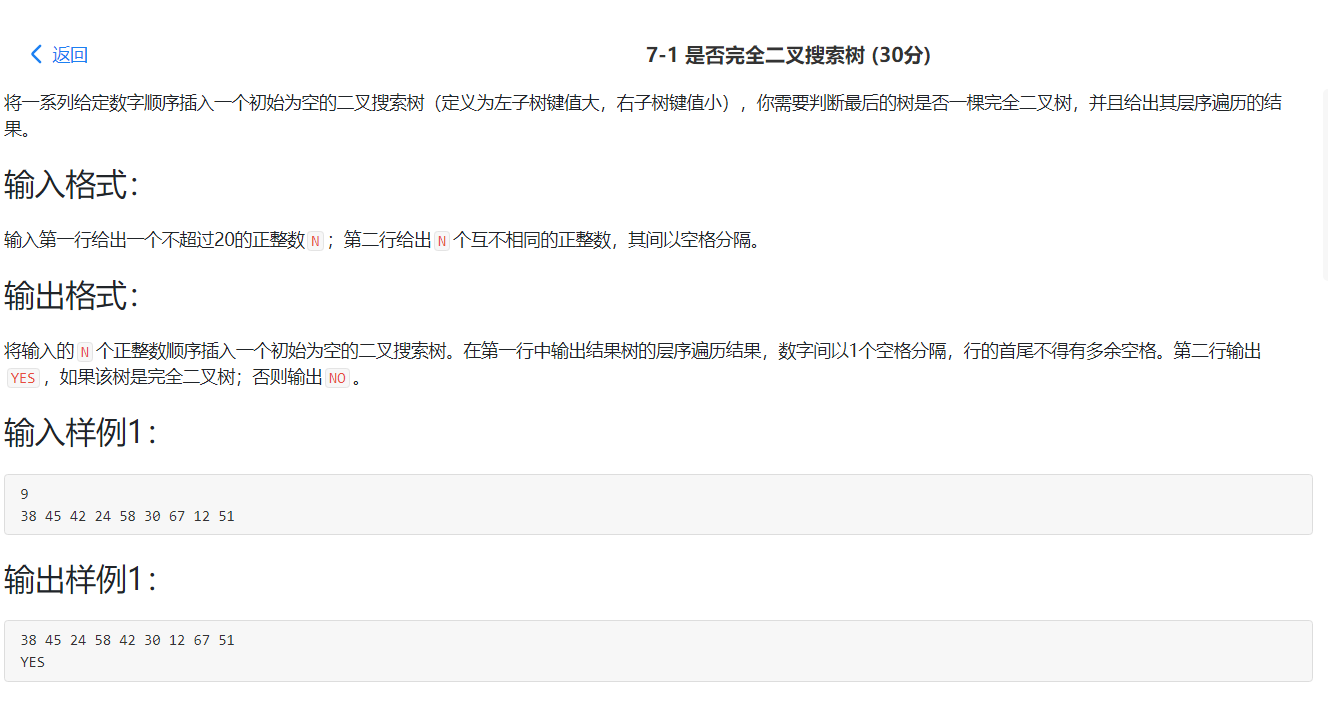
2.1 题目一:7-1是否完全二叉搜索树
2.1.1 该题的设计思路
二叉搜索树的特点:
左子树<根节点<右子树
完全二叉树的特点:
树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
首先来理解一下完全二叉树,下面左图是完全二叉树,有图不是完全二叉树

接着,我们按照层次遍历的方法把左图和右图分别入队列进行观察,遇到一个节点,就把它的左右孩子入队,然后当前节点出队。
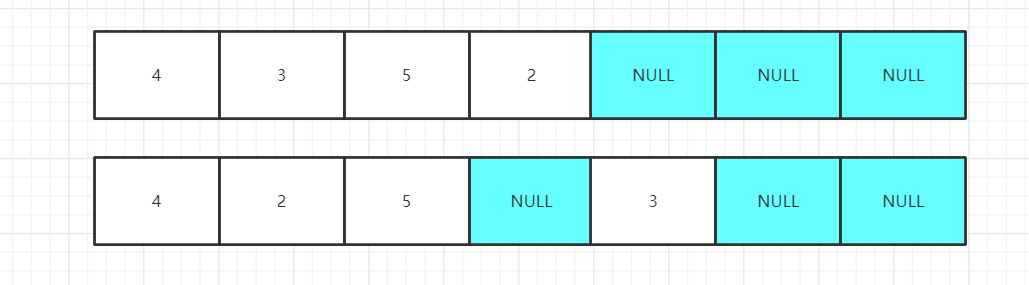
通过上面,是否发现了一个特点,如果是完全二叉树,遇到第一个NULL之后,后面就不会再出现非空节点,如果不是完全二叉树,则在NULL后面会出现非空节点。
根据上面的思路,我们要做的步骤是
1.建立一棵二叉搜索树,采用树结构
2.需要队列,来判断是否完全二叉搜索树
2.1.2伪代码
int main()
{
BinTree T;
建立一棵二叉搜索树,并返回根节点给T
如果是完全二叉树
输出层次遍历序列
输出yes
否则
输出层次遍历序列
输出no
}
BinTree BuiddTree()
{
BinTree BST;
初始化BST为空,
输入节点个数n
for i=0 to i=n-1
输入节点关键字
并Insert到BST这棵树中
}
BinTree Insert(BinTree BST, int X)
{
if BST是NULL
申请一个节点T,左右孩子置为空,并赋值为x
else if 当前节点BST对应的关键字比x小
递归往右孩子寻找
else 当前节点BST对应的关键字比x大
递归往左孩子寻找
return 根节点BST;
}
bool IsBinaryTree(BinTree t)
{
if 是空树,返回true,空树也是完全二叉树
queue<BinTree>qu;
把根节点t入队
while(t!=NULL)
{
取队头节点t,并出队
把t的左右孩子节点入队,直到遇到第一个NULL节点
}
while(队列不空)
{
检查后面是否有非空节点
取队头节点t,并出队
if(t是非空节点)
return false;
}
}
void LevelderTraversal(BinTree t)
{
queue<BinTree>Levelqu;
取根节点入队
while(队列不空)
{
取队头节点temp,并出队
if temp不为空
把左右孩子入队
并输出当前节点的关键字
}
}
2.1.3 PTA提交列表

Q1:思路错误,如何辨别完全二叉树的代码思路是错的,如果叶子节点的最右边是由关键字的,我的代码弄出来会是个yes的答案,本来还想着,用一个n来存储每一层的节点个数,对每一次层进行判断,但是我觉得如果碰到大数据的情况,n的时间效率会非常差,而且本身这样的思路效率也不好,于是后来引进了队列
Q2:层次遍历输出序列控制好,输出层次遍历并没有特定的一个函数,而是和判断完全二叉树一起的,所以会容易导致错误
2.1.4本题知识点
1.学会二叉搜索树的建立
2.如何判断完全二叉树
3.本题时间复杂度:O(n)
2.1.5 代码实现
我的代码
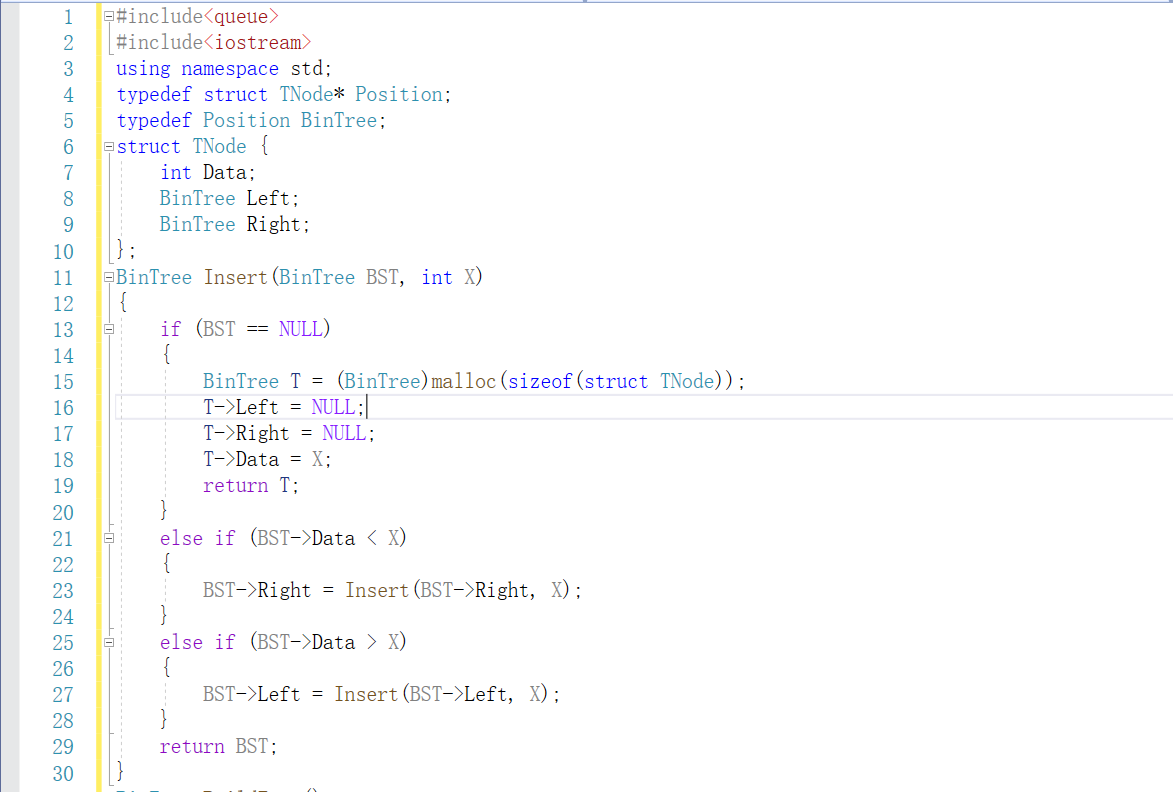
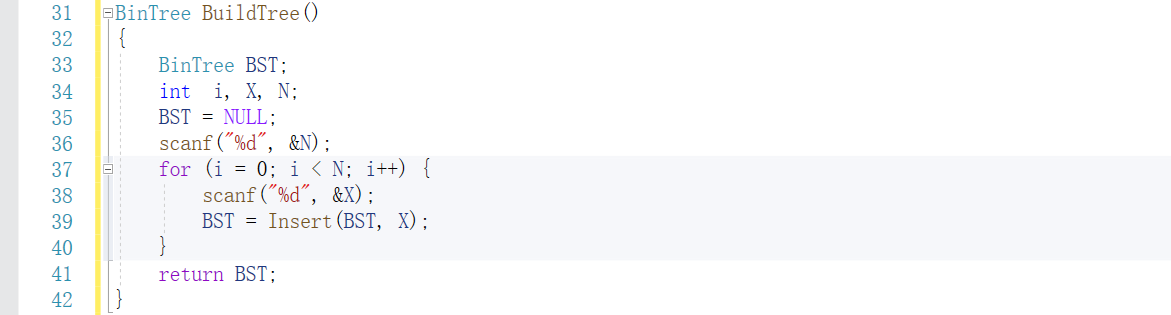

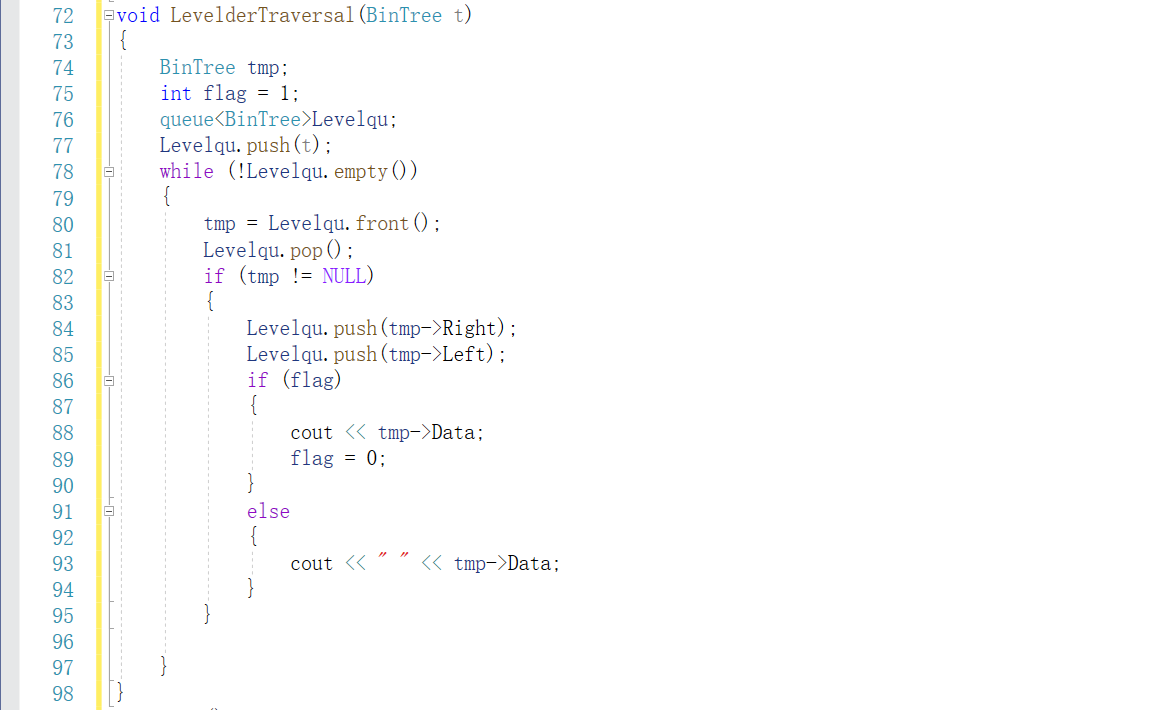

同学代码:
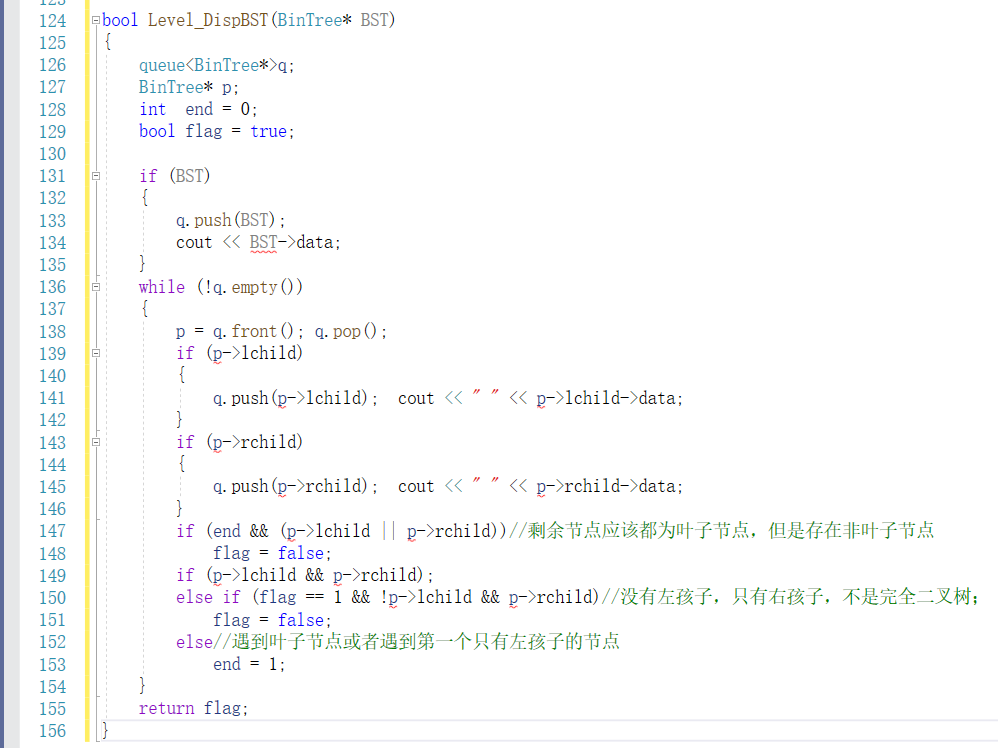
上面是同学代码的核心部分,同学代码整体上比我的简洁很多,因为它可以在做判断的时候,并输出先序遍历,思路和我的也不一样。
同学思路:
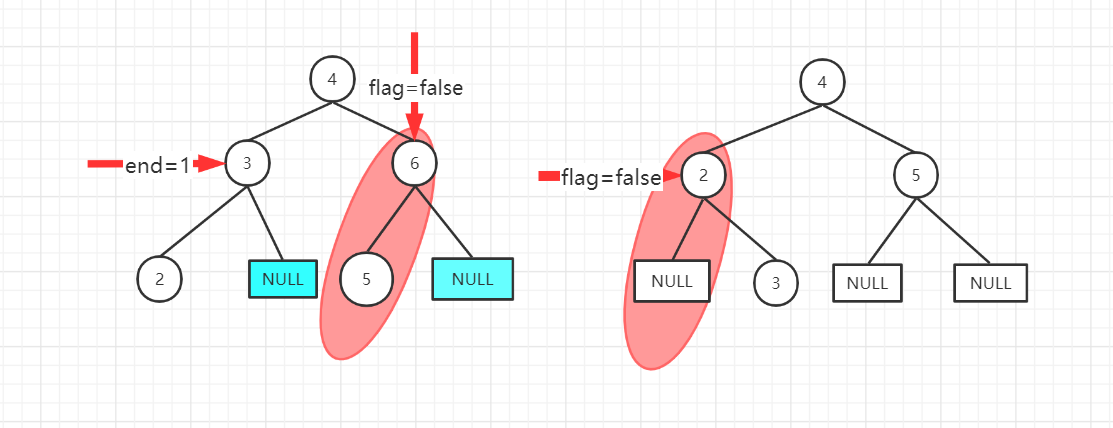
1.flag用来判断是否是完全二叉树
2.end用来找出第一个叶子节点,或者只有左孩子的节点,如果end置为1,说明后面的都将是叶子节点,那么如果后面出现了节点有左孩子或者右孩子的,那么说明就不是完全二叉树,如果出现了一个节点有右孩子而没有左孩子,也是错的。
!
2.2题目二:7-2 二叉搜索树的最近公共祖先
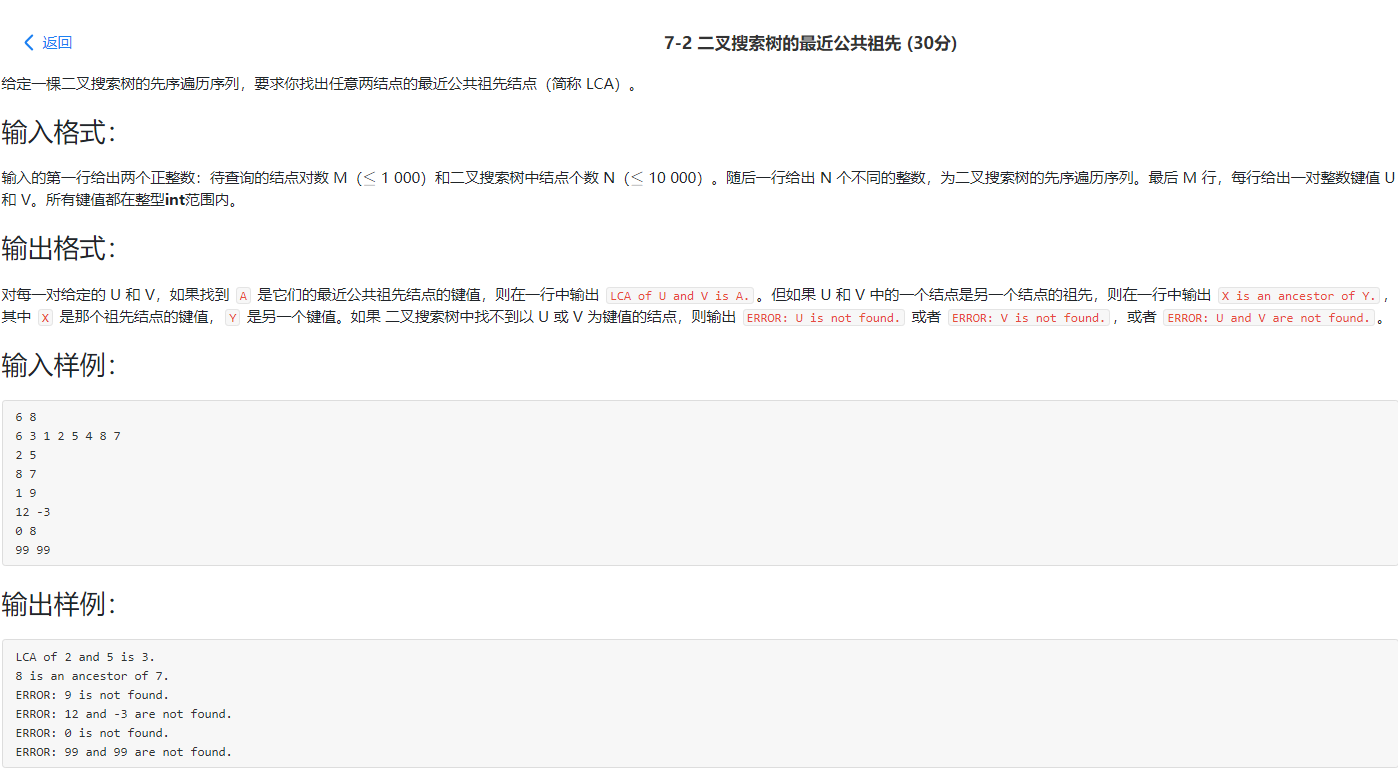
2.2.1该题的设计思路
1.解决二叉搜索树的先序遍历来建树
2.解决寻找最近公共祖先的问题
解决第一个问题:
第一种方法,根据先序遍历的序列,按照按照二叉搜索树的方法进行建树,得到的先序遍历和输入的先序遍历是一样的
Tree Insert(Tree BST, int X)
{
if (BST == NULL)
{
Tree T = (Tree)malloc(sizeof(struct TreeNode));
T->Left = NULL;
T->Right = NULL;
T->Key = X;
return T;
}
else if (BST->Key < X)
{
BST->Right = Insert(BST->Right, X);
}
else if (BST->Key > X)
{
BST->Left = Insert(BST->Left, X);
}
return BST;
}
第二种办法:
给的是先序遍历的序列,即按照根左右的办法进行遍历,我们在学到树的那一章,有学到根据先序遍历中序遍历来建一棵树的递归算法,有人可能会很奇怪,因为这道题里,只给了先序遍历的代码,并没有中序遍历,事实上,这道题,还有一个隐藏条件,就是二叉搜索的特点,它让我们不需要中序遍历,就可以建出一棵树,首先,先理解,我们递归建树的最重要要素是什么,就是"根"节点,对于每进入一个新的递归,就把当前节点看成是我们还未建树的根节点,那么,这个根节点的特点是啥,如果后面比他小的树,就是它的左子树,遇到的第一个比它大的数,就是它的右子树。

解决第二个问题:
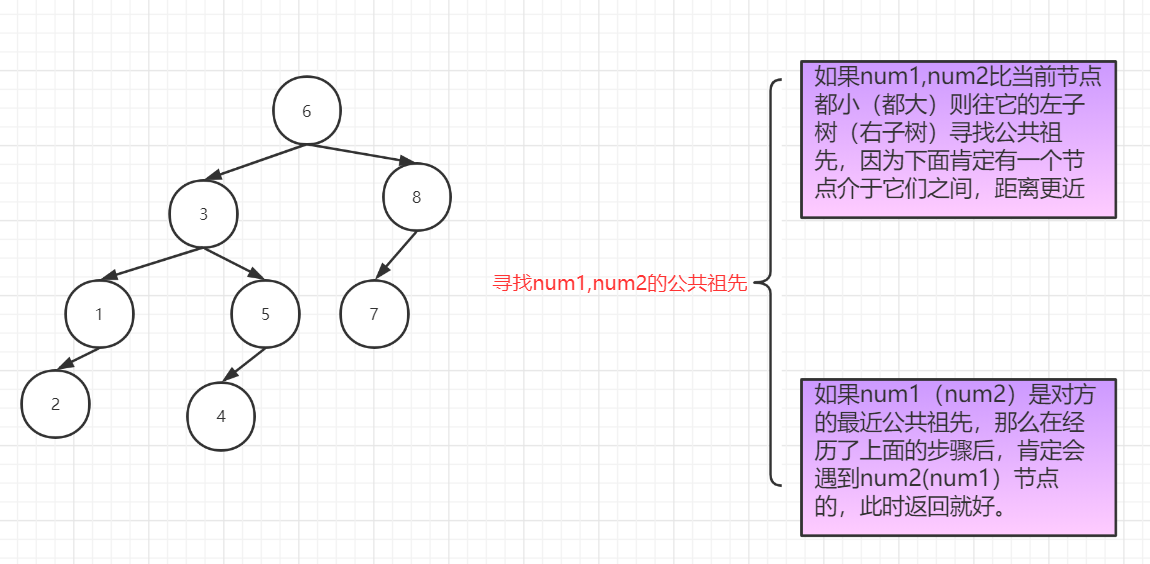
Tree CreateTree(Tree BST, int* preorder, int len)
{
int i;
if (len == 0) return NULL;
BST = (Tree)malloc(sizeof(TreeNode));
BST->Key = *preorder;
BST->Left = BST->Right = NULL;
for (i = 0; i < len; i++)
{
if (preorder[i] > BST->Key)
{
break;
}
}
BST->Left = CreateTree(BST->Left, preorder + 1, i - 1);
BST->Right = CreateTree(BST->Right, preorder + i, len - i);
return BST;
}
2.2.2伪代码
int main()
{
Tree BST=NULL;
输入n,N;
for i=1 to i=N
输入先序序列
建立一棵二叉搜索树,并返回给BST;
for i=1 to i=n
输入u,v
返回查找公共祖先LCA的结果ans
如果ans=u,那么u是v的祖先
如果ans=v,那么v是u的祖先
如果既不等u也不等v,那么ans是u和v的祖先
end for
}
int LCA(Tree T, int u, int v)
{
flagL,flagR用来标记u,v是否在树中,初始化为1
如果u不在树中,flagL置为-1
如果v不在树中,flagR置为-1
如果flagR,flagL都为-1,输出提示,并放回error
如果flagR为-1,输出提示,并放回error
如果flagL为-1,输出e提示,并放回error
如果u>v,将u与v互换
while(T!=NULL)
{
if 树节点小于u
在右子树找
else if 树节点大于v
在左子树找
else
返回公共祖先
}
}
Tree CreateTree(Tree BST, int* preorder, int len)
{
申请一个节点BST,并对其进行赋值
for i=0 to i=len-1
在preorder里找到第一个大于BST->key的值,然后break
用来区分左右子树
先递归建立左子树,范围是preorder+1到i-1
然后递归建立右子树,范围是preorder+i,len-i
}
2.2.3 PTA提交列表
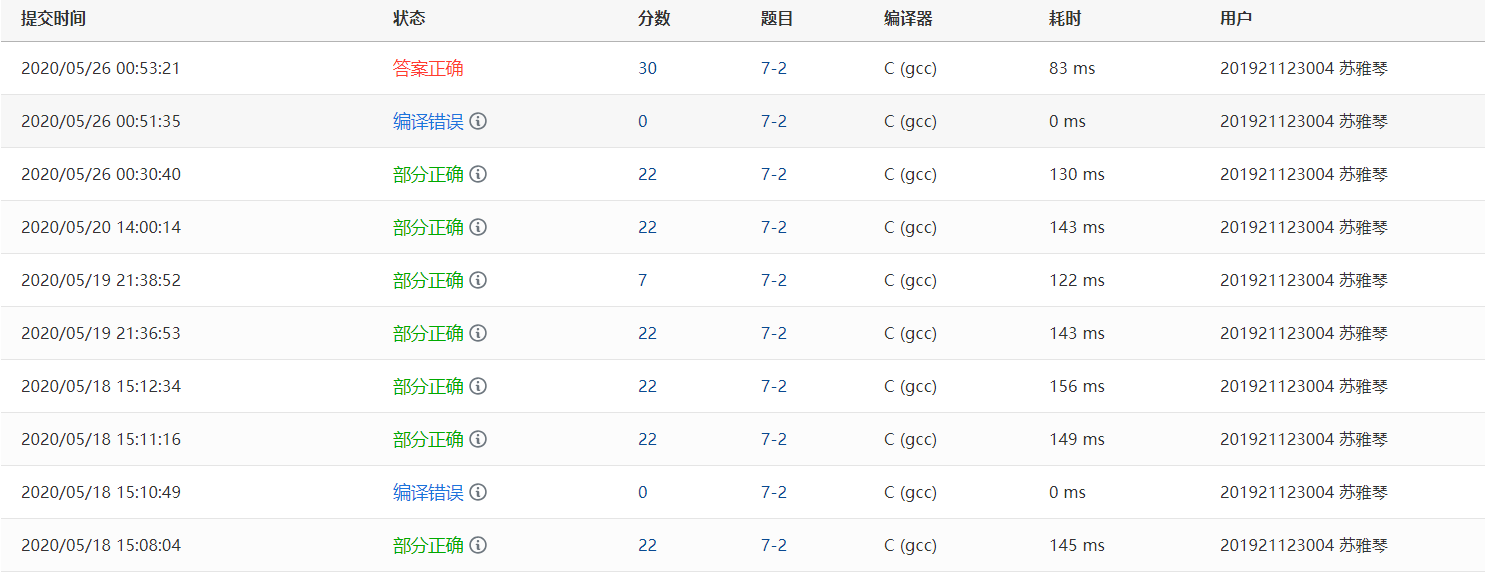
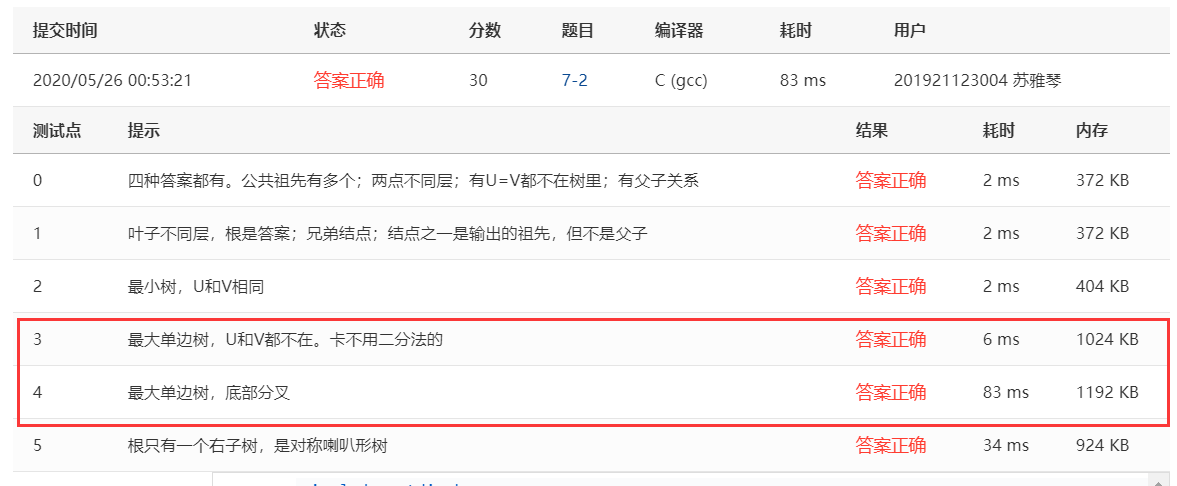
Q:这道题,我一直过不起的是第三和第四个测试点,告诉我运行超时,老师在上课有讲过思路,和他的差不多,不过有一个东西被我忽略了,就是建树,我一直以为这道题建树不是难点,却没想到这道题如果建树没建好,就会导致超时,我本来就是用上面的第一种方法建树的,但是没意思到时它出错了,所以一直在LCA里做文章,却都过不去,然后取网上查找了一下,看到一篇和我一样错误的,说一直有两个测试点过不去,他指出时因为建树的不对,我这才清楚,想想这两个建树的方法,方法一,每次都要遍历出一条路径,在叶子节点插入,这样,在数据量大的情况下,时间效率也很可怕,而方法二不用,因为总的算起来,他就递归len-1次,就是节点的个数
2.2.4 本题知识点
1.如何用二叉搜索树的先序遍历建树,并且效率更高
2.查找两个节点的最近公共祖先
3.学会二叉搜索树查找代码的实现
2.2.5 代码实现
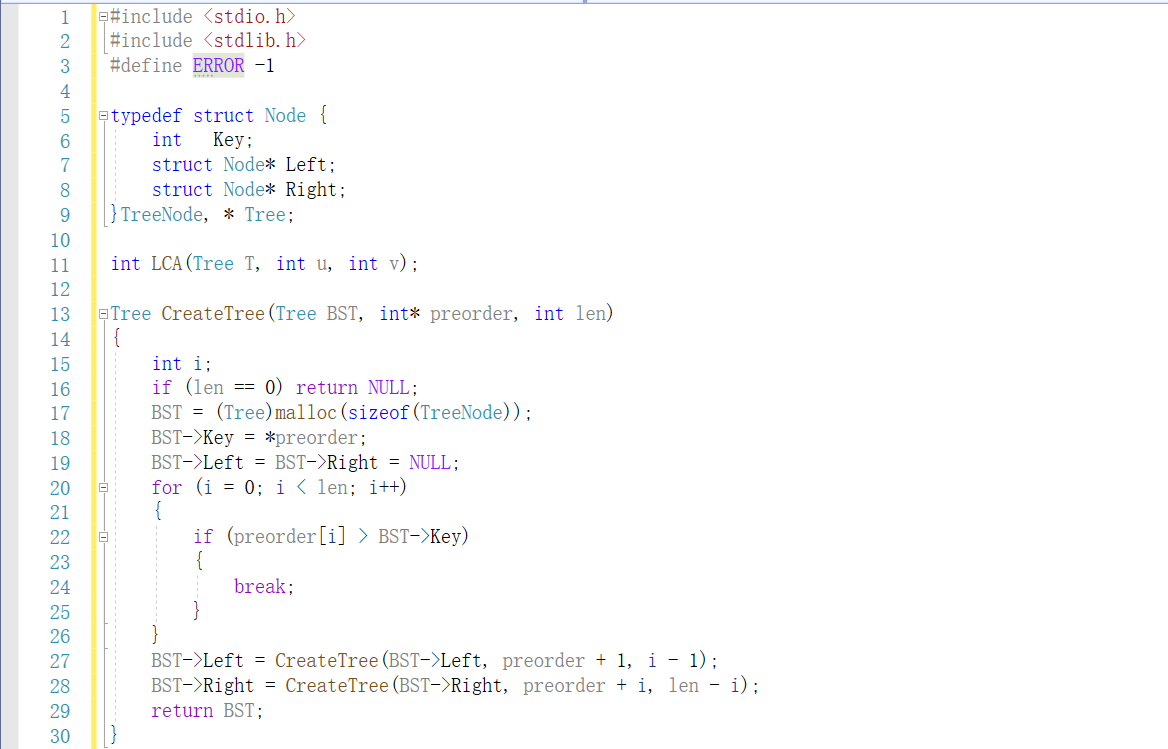

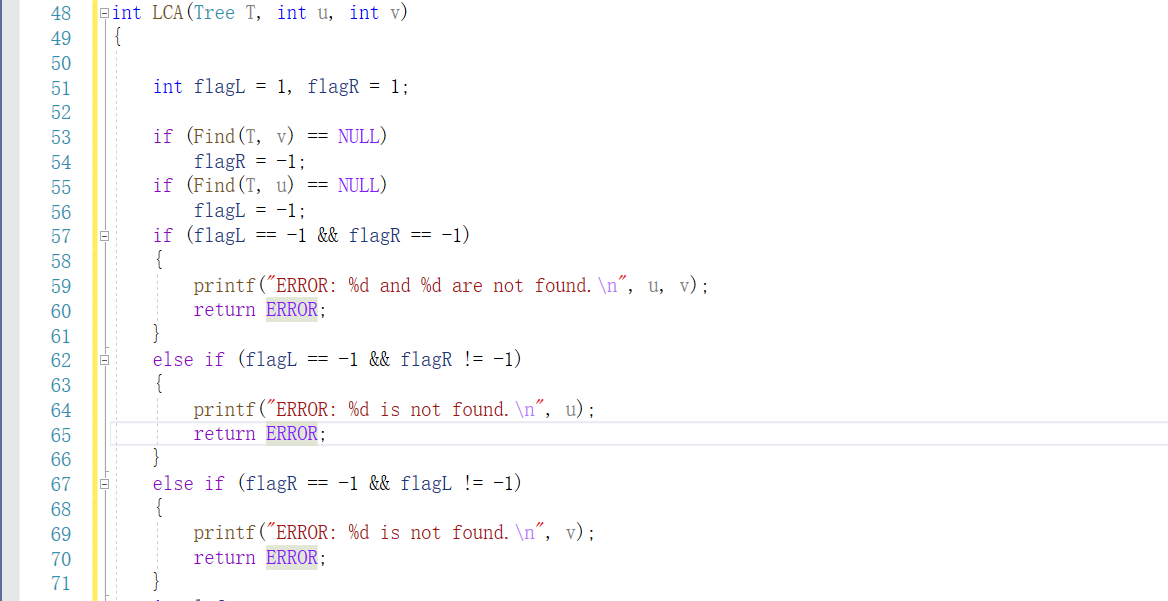

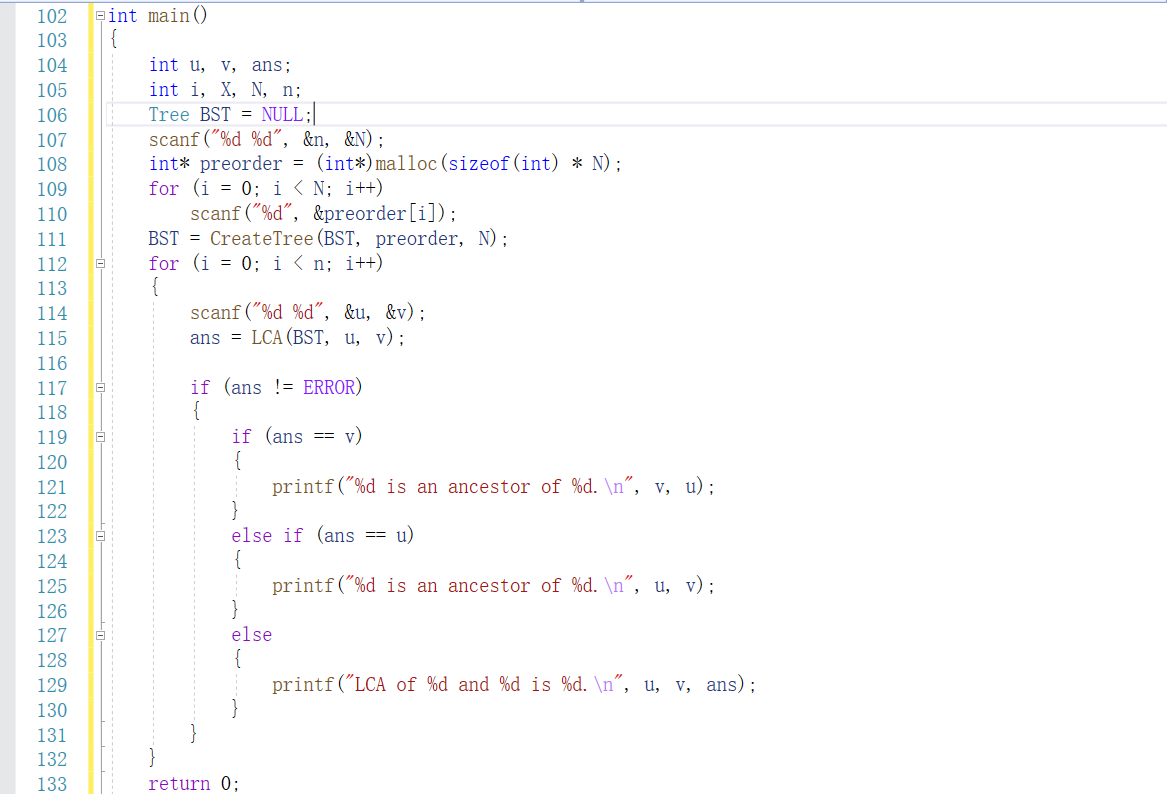
2.3题目三:7-5(哈希链) 航空公司VIP客户查询
2.3.1该题的设计思路
这道题的思路是建好哈希链就好,比较难的是对于数据的处理
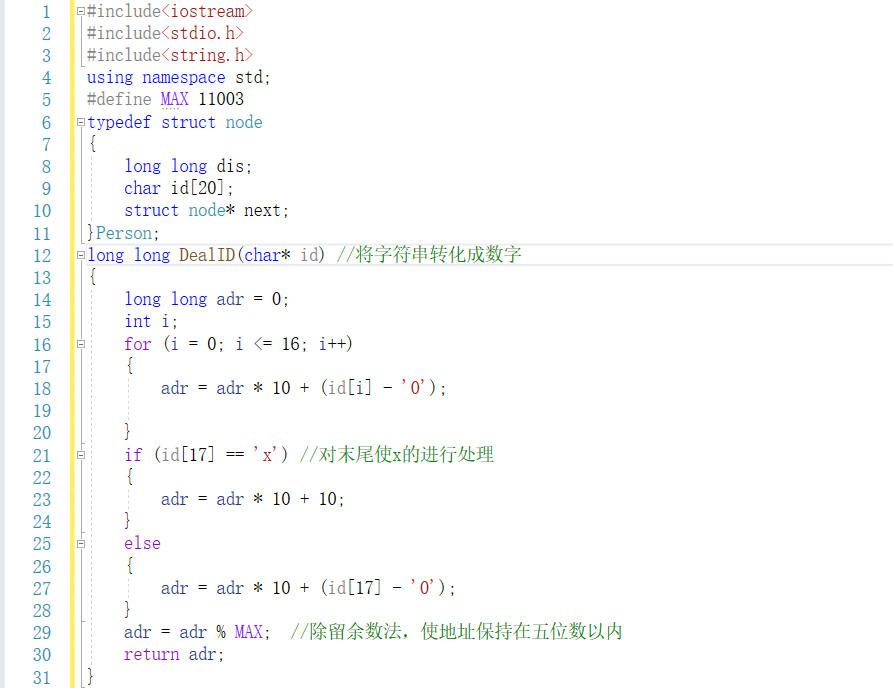
1.对于身份证的处理,将字符串转换成数字,然后根据除留余数法,将它作为地址注意一下变量的类型
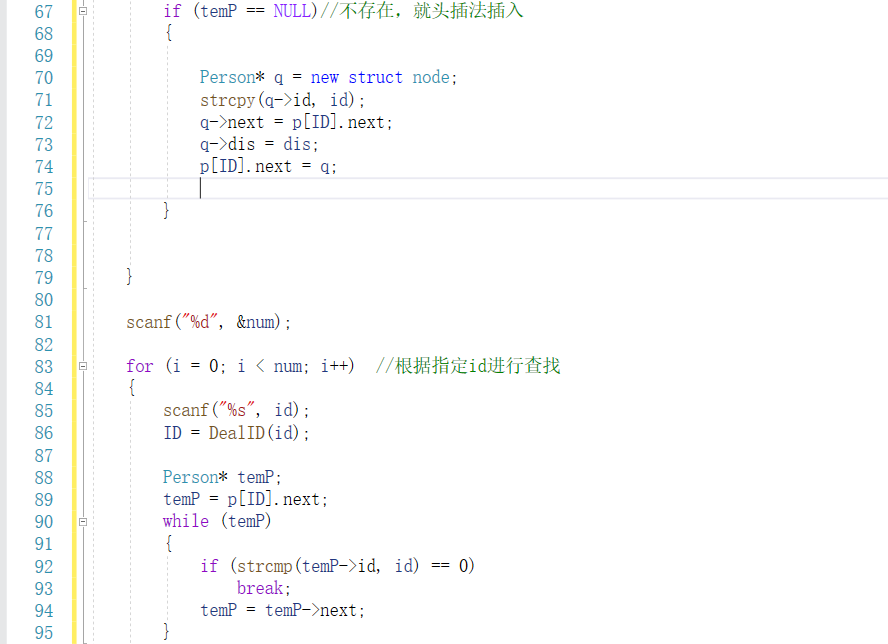
2.建哈希链,将得到的新id作为地址,然后在对应地址的哈希链里查找,如果有,加上对应的dis值,如果没有,就用头插法进行插入
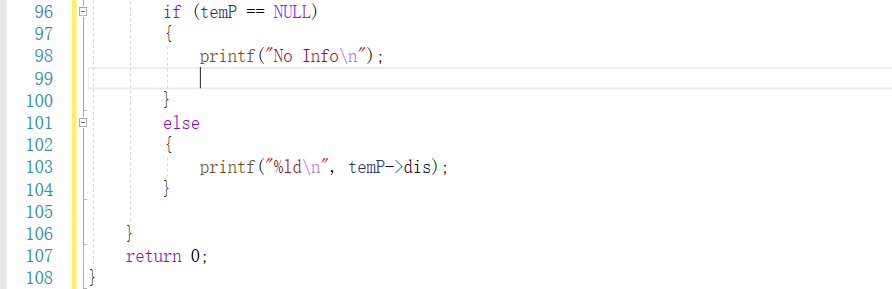
3.最后查找,也是根据转换后的id进行转换
2.3.2伪代码
int main()
{
输入个数n和k
for i=0 to i=MAX
对哈希链进行初始化
end for
for i=0 to i=n-1
输入id和dis
将字符串id转换成地址ID
指针temp,指向对应ID的第一个表头节点
while(temp)
{
对这条链进行遍历
如果有找到,加上对应的dis值
}
如果没找到,new一个新节点,通过头插法插入到地址ID对应的链里
end for
输入num
for i=0 to i=num-1
输入身份证id
将身份证转换成数字ID
同样temp指向地址ID对应的第一个表头结点
while(temp)
{
遍历,如果找到,输出dis
}
没找到,输出No Info
end for
}
2.3.3 PTA提交列表


1.一开始,没有用哈希的做法做,建了一个邻接表,把身份证用string存储起来,然后最后遍历一遍。所以最后对于测试点1和测试点2超时了,于是后来换成了哈希链做
2.换成哈希链后有一个比较懵逼的地方,就是数据处理,可能是对于哈希建法还是特别熟悉,所以将身份证转换成数字后,就有点懵逼不知道干啥了,忘记了除留余数法,当时还纠结数据这么大,怎么当下标,现在觉得被自己蠢哭了
2.3.4 本题知识点
1.这道题,容易超时的一个很大原因是用了c++的cin来输入字符串类型,一开始我是不知道的,因为数据结构开始,就老师就推荐我们用cin,因为简单,且它会自动识别类型,后来同学和我说,这道题不能用cin,因为会容易超时,后来我也去查看了网上的介绍,当数据量较大时,cin和cout的耗时可能会是scanf,printf的好几倍
原因:
因为C++为了兼容C,保证程序在使用了std::printf和std::cout的时候不发生混乱,将输出流绑到了一起,即cin绑定的是cout,每次执行 << 时都要调用flush,增加了IO负担。这就意味着,先把要输出的东西存入缓冲区,再输出缓存,从而导致效率降低,如果我们还是想用cin,cout的话,只需要把他们解除绑定即可
#include <iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);//接触绑定
}
2.第二个知识点,就是对数据巧妙地处理,因为身份证中包含x,它不是数字,所以处理的时候,可以把它看成10,或11等等,单独处理
2.3.5 代码实现




 浙公网安备 33010602011771号
浙公网安备 33010602011771号