洛谷题解P4994 终于结束的起点
Update
2020.11.20
在文末 (Some Questions) 指出的问题已经有了答案 :
-
我的代码必须开
long long，要不然#9会WA，显示Too short on line 1- 这里题目中明确提到了
对于 \(100\%\) 的数据，\(2 \leq M \leq 706150\)
- 显然，\(m^2\) 会爆
int，这也是之前考虑不周的地方。
-
在不开
long long的情况下，将i<=m*m改为i<=m^2可以AC，且用时较long long来说还短 （数据问题 ？）- 这应该是数据问题，在没有数据的情况下，暂时无法证实。
原题传送门
Description
给定 \(m\) ，求使 \(fib(n)\bmod m=0\) 且 \(fib(n+1)\bmod m=1\) 的最小 \(n\) 值 \((n>0)\)，这里的 \(fib(n)\) 为 Fibonacci 数列中的第 \(n+1\) 个数的值。
注 :
「这里的 \(fib(n)\) 为 Fibonacci 数列中的第 \(n+1\) 个数的值。」
这一句话相信不难理解，因为 Fibonacci 数列 是从 \(fib(0)\) 开始的。
附 :
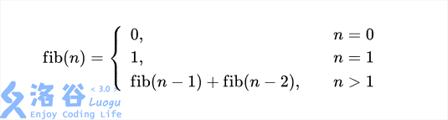
Solutions and Code
30pts
直接计算出 \(fib(n)\) ，然后按照题意进行判断。
#include<iostream>
#include<cstdio>
using namespace std;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+(ch&15);
ch=getchar();
}
x*=f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m;
inline int fib(int n){
if(n==0) return 0;
if(n==1) return 1;
if(n>1) return fib(n-1)+fib(n-2);
}
int main(){
int m;
read(m);
for(int i=1;;i++){
if(fib(i)%m==0 && fib(i+1)%m==1){
write(i);
return 0;
}
}
return 0;
}
70pts
根据 Fibonacci 数列的定义，预处理出 \(fib(i)\bmod m\) 当 \(i\in [0,m^2]\) 时的值 ，然后遍历查找。
注 : 题目中明确提到了
在 \(M^2\) 次计算后一定出现过循环。
因为这里已经取完模，所以说可以进一步从 \(i\in [0,+\infty)\) 优化成 \(i\in [0,m^2]\)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+(ch&15);
ch=getchar();
}
x*=f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n,m;
inline int fib(int n){
if(n==0) return 0;
if(n==1) return 1;
if(n>1) return fib(n-1)+fib(n-2);
}
int main(){
int m;
read(m);
int f[m*m+1];
memset(f,0,sizeof(f));
f[0]=0,f[1]=1;
for(int i=2;i<=m*m;i++){
f[i]=(f[i-2]+f[i-1])%m;
//write(f[i]),putchar(' ');
}
for(int i=1;;i++){
if(f[i]==0&&f[i+1]==1){
write(i);
return 0;
}
}
return 0;
}
100pts
利用滚动数组，把预处理的 \(f\) 数组转化成以下三个变量 : \(now,next,temp\)。
- \(now\) 表示当前数的 \(fib\) 值
- \(next\) 表示下一个数（即 \(now+1\)） 的 \(fib\) 值
- \(temp\) 表示 \(now+2\) 的 \(fib\) 值 \(\to \dfrac{(now+next)}{2}\)
其实这三个变量中，\(next\) 才是真正意义上的当前数的 \(fib\) 值，因为 \(fib(n)\) 表示的是在 Fibonacci 数列中第 \(n+1\) 个数的值
所以在判断时，应为 :
if(next==0 && temp==1){
write(i);
return 0;
}
//i from 1 to m^2
故 Code :
#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+(ch&15);
ch=getchar();
}
x*=f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
signed main(){
int m;
read(m);
int now=0,next=1;
int temp;
for(int i=1;i<=m*m;i++){
temp=(now+next)%m;
if(next==0 && temp==1){
write(i);
return 0;
}
now=next;
next=temp;
}
return 0;
}
Some Questions (To Update)
在 \(100pts\) 的做法中，我发现有这样几个问题 :
- 我的代码必须开
long long，要不然#9会WA，显示Too short on line 1
int 提交记录 - 在不开
long long的情况下，将i<=m*m改为i<=m^2可以AC，且用时较long long来说还短 （数据问题 ？）
i<=m^2 提交记录
