洛谷题解P3378 【模板】堆 暨 浅谈堆
原题传送门
\(\text{Solution}\)
一道堆的模板题,借此机会来讲一下堆的概念及基本操作。
\(1\).概念
堆为一种数据结构,即用数组来实现一棵 完全二叉树
有小根堆和大根堆两种。
- 大根堆 : 根节点点权最大
- 小根堆 : 根节点点权最小
- 所有的堆都满足一下一条性质 : 堆中某个节点的值总是不大于或不小于其父节点的值
当然,在 \(\text{STL}\) 中有其对应的数据结构(优先队列实现)
这里主要来说手写堆(用数组实现)
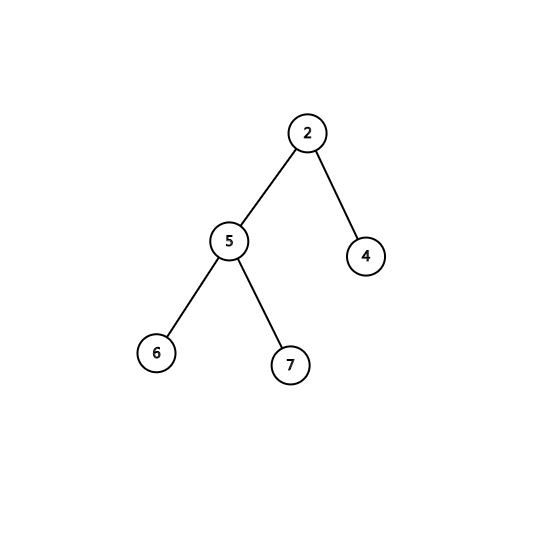
.png)
以上分别是一张小根堆示意图和一张大根堆示意图。(图中点内数字表示点权)
\(2\).操作
\((1).push\) (把一个元素 \(x\) 加入堆)
思想如下 :
- 把 \(x\) 放进堆尾
- 比较当前节点与其父节点的大小
- 如是小根堆,即当当前节点比其父节点点权小时,交换当前节点与其父节点,循环往复,直至满足小根堆的要求为止。
- 如实大根堆,即当当前节点比其父节点点权大时,交换当前节点与其父节点,循环往复,直至满足大根堆的要求为止。
则我们可以得到以下代码 :
inline void push(int p){
int fa,now;
heap[++cnt]=p; //加入堆
now=cnt; //注意初始化为当前堆尾
while(now>1){
fa=now>>1; //取其父节点
if(heap[now]<heap[fa]){ //小根堆为 "<" ,大根堆为 ">"
swap(heap[now],heap[fa]);
now=fa;
}
else return;
}
}
\((2).delete\)(删除堆中的最值节点)
对于这个问题,分两种情况讨论
- 小根堆
- 删除最小值
- 把堆尾元素的值覆盖到堆的根节点(小根堆最小值)上,相当于完成了删除操作。
- 比较当前节点与其子节点的大小,当当前节点比其儿子大时,交换当前节点与其儿子的值,循环往复,直到满足小根堆的要求为止。
- 特别地,当此节点有两个子节点时,需要找出较小的那个,完成交换
- 删除最大值
- 直接删除堆尾元素
- 删除最小值
- 大根堆
- 删除最小值
- 直接删除堆尾元素
- 删除最大值
- 把堆尾元素的值覆盖到堆的根节点(大根堆的最大值)上,相当于完成了删除操作。
- 比较当前节点与其子节点的大小,当当前节点比其儿子小时,交换当前节点与其儿子的值,循环往复,直到满足大根堆的要求为止。
- 特别地,当此节点有两个子节点时,需要找出较大的那个,完成交换
- 删除最小值
则我们可以得到以下代码 :
inline void deleted(){
heap[1]=heap[cnt--]; //覆盖,相当于删除,注意为 "cnt--"
int now=1,son; //覆盖的是堆头,从堆头开始遍历
while(now*2<=cnt){ //保证当前节点会有子节点
son=now*2; //定义左儿子
if(son<cnt && heap[son+1]<heap[son]) son++;
//找两个子节点中的最值,在 "heap[son+1]<heap[son]" 中,小根堆为 "<" ,大根堆为 ">"
if(heap[son]<heap[now]){ //小根堆为 "<" ,大根堆为 ">"
swap(heap[son],heap[now]);
now=son;
}
else return;
}
}
本题 \(Code\)
#include<iostream>
#include<cstdio>
using namespace std;
const int Maxn = 1e6+10;
inline void read(int &x){
int f=1;
char ch=getchar();
x=0;
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
x*=f;
}
int n;
int op;
int x;
int heap[Maxn],cnt;
inline void push(int p){
int fa,now;
heap[++cnt]=p;
now=cnt;
while(now>1){
fa=now>>1;
if(heap[now]<heap[fa]){
swap(heap[now],heap[fa]);
now=fa;
}
else return;
}
}
inline void deleted(){
heap[1]=heap[cnt--];
int now=1,son;
while(now*2<=cnt){
son=now*2;
if(son<cnt && heap[son+1]<heap[son]) son++;
if(heap[son]<heap[now]){
swap(heap[son],heap[now]);
now=son;
}
else return;
}
}
inline void swap(int &a,int &b){int t=a;a=b;b=t;}
int main(){
read(n);
for(int i=1;i<=n;i++){
read(op);
if(op==1){
read(x);
push(x);
}
else if(op==2) printf("%d\n",heap[1]);
else deleted();
}
return 0;
}
本文欢迎转载,转载时请注明本文链接


