codeforces 557 D. Vitaly and Cycle 组合数学 + 判断二分图

D. Vitaly and Cycle

 

 

 

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

After Vitaly was expelled from the university, he became interested in the graph theory.

Vitaly especially liked the cycles of an odd length in which each vertex occurs at most once.

Vitaly was wondering how to solve the following problem. You are given an undirected graph consisting of n vertices and m edges, not necessarily connected, without parallel edges and loops. You need to find t — the minimum number of edges that must be added to the given graph in order to form a simple cycle of an odd length, consisting of more than one vertex. Moreover, he must find w — the number of ways to add t edges in order to form a cycle of an odd length (consisting of more than one vertex). It is prohibited to add loops or parallel edges.

Two ways to add edges to the graph are considered equal if they have the same sets of added edges.

Since Vitaly does not study at the university, he asked you to help him with this task.

Input

The first line of the input contains two integers n and m (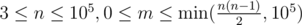 — the number of vertices in the graph and the number of edges in the graph.

Next m lines contain the descriptions of the edges of the graph, one edge per line. Each edge is given by a pair of integers a_i, b_i (1 ≤ a_i, b_i ≤ n) — the vertices that are connected by the i-th edge. All numbers in the lines are separated by a single space.

It is guaranteed that the given graph doesn't contain any loops and parallel edges. The graph isn't necessarily connected.

Output

Print in the first line of the output two space-separated integers t and w — the minimum number of edges that should be added to the graph to form a simple cycle of an odd length consisting of more than one vertex where each vertex occurs at most once, and the number of ways to do this.

Examples

Input

4 4
1 2
1 3
4 2
4 3

Output

1 2

Input

3 3
1 2
2 3
3 1

Output

0 1

Input

3 0

Output

3 1

Note

The simple cycle is a cycle that doesn't contain any vertex twice.

 

 

 

题意：

给出一个图，无重边和自环

设t为要加的最小的边数，使得图有奇数个节点的环，环中的每一个节点只经过一次

设w为加满足条件的t条边的方案数

输出t w

 

思路：

考虑这个图的每一个节点的度deg

1.最大的度 = 0，说明图没有边，图的最长路为0，那么

　　t = 3,w = C(n,3)

2.最大的度 = 1，说明图的最长路为1，那么

　　t = 2,w = m * (n - 2)

3.最大的度 > 1，说明图的最长路>1,那么

　　(1).如果原图有奇数个节点的环，那么

　　　　t = 0,w = 1

　　(2).如果原图没有奇数个节点的环，那么

　　　　t = 1,w = ?

 

如何判断原图有没有奇数个节点的环呢？

我们发现，

如果原图没有奇数个节点的环，那么原图就是一个2分图

如果原图有奇数个节点的环，那么原图就不是一个2分图

 

所以用染色法就可以知道原图是不是一个2分图啦

那上面讨论中的？的值是多少呢？

当原图是一个2分图的时候，

对于图的每一个联通分量，我们把这个联通分量的节点分成了2部分，

分别有x，y个节点，那么ans += C(x,2) + C(y,2)

 

注意，

是对每一个联通分量，分别得到x,y,然后更新ans

而不是对整个图求x,y

因为对于我们选择加入的这一条边的2个端点，一定是要在同一个联通分量中的

 

代码：

                                            
  //File Name: cf557D.cpp
  //Author: long
  //Mail: 736726758@qq.com
  //Created Time: 2016年07月08日 星期五 20时38分29秒
                                   
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <queue>

#define LL long long

using namespace std;

const int MAXN = 100000 + 3;

int deg[MAXN];
int is[MAXN];
bool flag;
queue<int> que;

struct Edge{
    int to,next;
}edge[MAXN << 1];
int head[MAXN],tot;

void init(){
    memset(head,-1,sizeof head);
    tot = 0;
    memset(deg,0,sizeof deg);
}

void addedge(int u,int v){
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
    edge[tot].to = u;
    edge[tot].next = head[v];
    head[v] = tot++;
}

void dfs(int p,int u,int x){
    is[u] = x;
    que.push(u);
    for(int i=head[u];~i;i=edge[i].next){
        int v = edge[i].to;
        if(v == p)
            continue;
        if(is[v] == x){
            flag = false;
            return ;
        }
        else if(is[v] == -1)
            dfs(u,v,x ^ 1);
    }
}

void solve(int n,int m){
    LL ans;
    int ma = -1;
    for(int i=1;i<=n;i++)
        ma = max(deg[i],ma);
    if(ma == 0){
        ans = (LL)n * (n - 1) * (n - 2) / 6;
        cout << "3 " << ans << endl;
    }
    else if(ma == 1){
        ans = (LL)m * (n - 2);
        cout << "2 " << ans << endl; 
    }
    else{
        ans = 0;
        memset(is,-1,sizeof is);
        flag = true;
        while(!que.empty())
            que.pop();
        for(int i=1;i<=n;i++){
            if(is[i] == -1){
                dfs(-1,i,0);
                int x = 0,y = 0, u;
                while(!que.empty()){
                    u = que.front();
                    que.pop();
                    if(is[u] == 0) x++;
                    else y++;
                }
                ans += (LL)x * (x - 1) / 2 + (LL)y * (y - 1) / 2;
            }
        }
        if(!flag)
            cout << "0 1" << endl;
        else
            cout << "1 " << ans << endl;
    }
    return ;
}

int main(){
    int n,m;
    while(~scanf("%d %d",&n,&m)){
        init();
        for(int i=0,u,v;i<m;i++){
            scanf("%d %d",&u,&v);
            addedge(u,v);
            deg[u]++;
            deg[v]++;
        }
        solve(n,m);
    }
    return 0;
}