红黑树笔记
问题:给一个无序的序列,找出指定值的位置?
比较简单的做法,对这个序列进行快排,接着使用二分查找。这样做确实能快速查找到,但如果我要给这个序列添加元素呢?维护这个序列的顺序的成本就大了。
此时我们可以使用一种叫二叉搜索树。
二叉搜索树
定义:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
这样我们就能解决上面遇到的给序列边加元素、边查找较快的方式。但如果这个序列初始就是递增或者递减的,那么这个树就会退化成单叉树,进行顺序查找。
例如:6、5、4、3、2、1
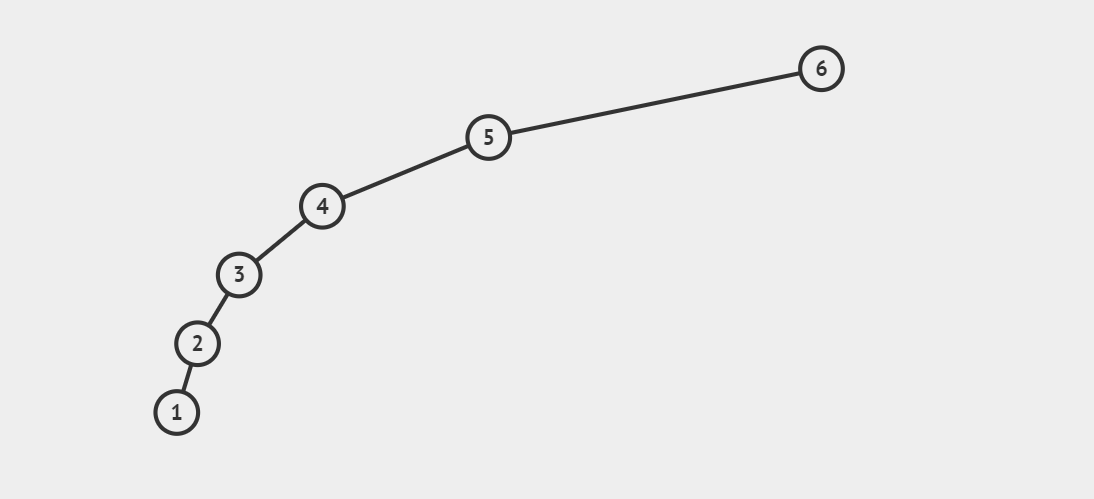
时间复杂度在:O(Log2n)到O(n)。
二叉搜索树会退化成线性,是因为没给给这个树定义一个规则,导致它可以没有边际的扩张,所以我们可以给这个树定一个规则,让他在有边界的前提下生长,对应于自然界也是如此,无规矩不成方圆。
此时平衡树就出现了。
AVL树
平衡二叉树之一。AVL树是二叉搜索树的改进。
在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是{\displaystyle O(\log {n})}
前置知识:
-
-
树的度:一棵树中,最大的节点的度称为树的度;
-
叶节点或终端节点:度为零的节点;
-
父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
-
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
-
兄弟节点:具有相同父节点的节点互称为兄弟节点;
-
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
-
树的高度或深度:树中节点的最大层次;
-
堂兄弟节点:父节点在同一层的节点互为堂兄弟;
-
节点的祖先:从根到该节点所经分支上的所有节点;
-
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
-
森林
操作步骤:每个节点都有自己的高度(叶子节点高度为0,非叶子节点的高度为左右节点最大高度+1)。新的节点N插入,首先会根据二叉搜索树的性质找到该插入的位置,接着会判断该节点X的左右节点高度差是否大于等于2,如果是的话,就要想办法给这个节点X进行平衡操作,让这个节点满足AVL性质。X节点平衡后,还需要往上判断该节点的父节点XP的左右节点是否满足条件,直到为根节点。这个通过递归就可实现。
现在的问题是:当发现节点X的左右节点树的高度差大于等于2的时候,我们应该通过怎样的平衡操作,让节点X所在树是满足AVL性质的。我们可以发现既然高度差太大,那可以将高度较高的一边,移走一些元素到另一边高度较低的一边,这样就可以解决问题了。(元素移动了位置,该树继续满足二叉搜索树的性质)
在这里引入左旋、右旋。
左旋:以某个结点(例如p)作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
右旋:以某个结点(例如p)作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变
左旋:以节点3进行左旋
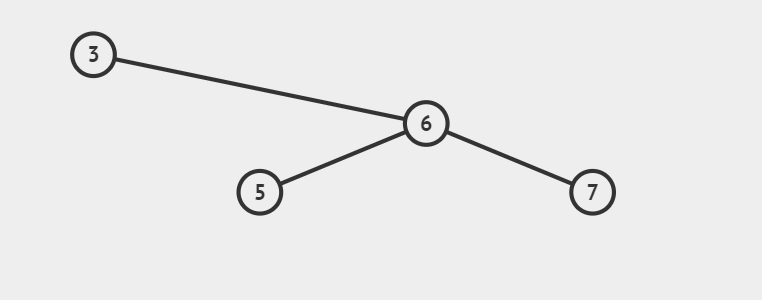
旋转后:
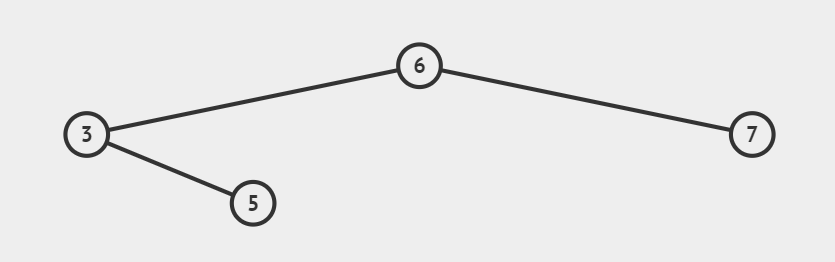
右旋:以节点6进行右旋
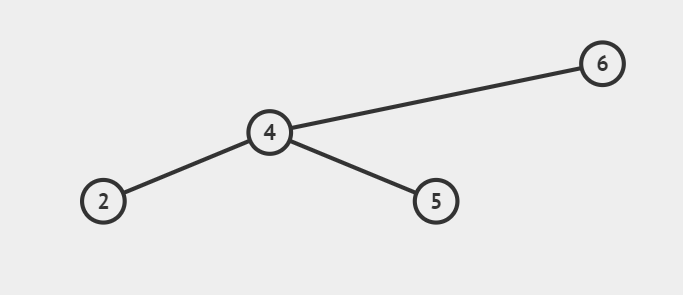
旋转后:

可以看到,旋转之后,能将树的左右子树的高度降低,而且树还继续满足二叉树的性质。
回到给AVL树新增节点的操作,首先找到插入的位置后,以该节点一直往上回溯,判断节点的左右子树高度差是否大于等于2。
这里就分以下情况:
左左型:

节点7的左子树高度为2,右子树高度为0,高度差为2。
操作:对节点7进行右旋,可以看到此时每个节点都满足AVL性质了。
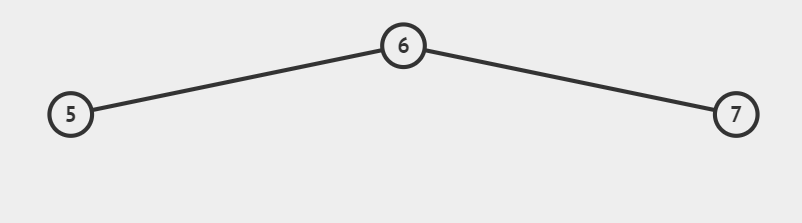
左右型:
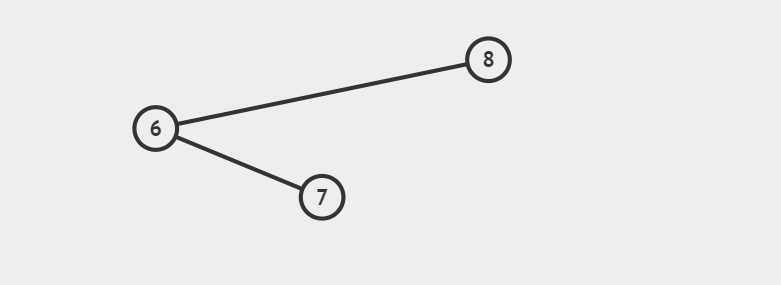
节点8的左子树高度为2,右子树高度为0,高度差为2。
操作:对节点6进行左旋,就转成左左型,最后对节点8进行右旋,可以看到此时每个节点都满足AVL性质了。
对节点6进行左旋:
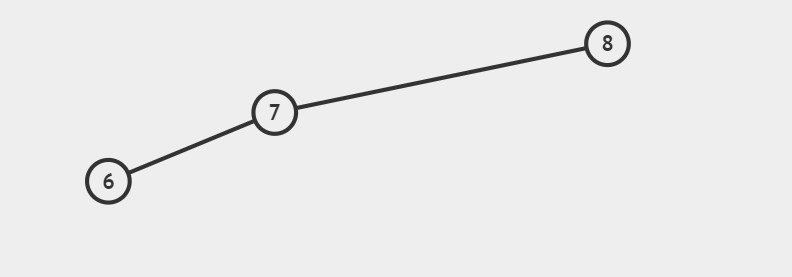
对节点8进行右旋:
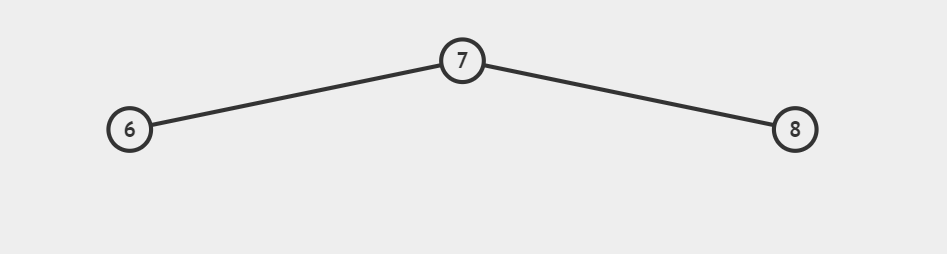
同样对于右右型,右左型亦是如此。
总结:
- 左-左型:做右旋。
- 右-右型:做左旋转。
- 左-右型:先做左旋,后做右旋。
- 右-左型:先做右旋,再做左旋。
左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。
右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
不管我们是执行插入还是删除操作,只要不满足AVL的条件,就要通过旋转来保持平衡,而旋转是非常耗时的,由此我们可以知道AVL树适合用于插入删除次数比较少,但查找多的情况。
代码:

//定义节点 class AvlNode { int data; AvlNode lchild;//左孩子 AvlNode rchild;//右孩子 int height;//记录节点的高度 } //在这里定义各种操作 public class AVLTree{ //计算节点的高度 static int height(AvlNode T) { if (T == null) { return 0; }else{ return T.height; } } //左左型,右旋操作 static AvlNode R_Rotate(AvlNode K2) { AvlNode K1; //进行旋转 K1 = K2.lchild; K2.lchild = K1.rchild; K1.rchild = K2; //重新计算节点的高度 K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1; K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1; return K1; } //右右型,进行左旋 static AvlNode R_Rotate(AvlNode K2) { AvlNode K1; K1 = K2.rchild; K2.rchild = K1.lchild; K1.lchild = K2; //重新计算高度 K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1; K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1; return K1; } //右-左型,进行右旋,再左旋 static AvlNode R_L_Rotate(AvlNode K3) { //先对其孩子进行右旋 K3.rchild = R_Rotate(K3.rchild); //再进行左旋 return L_Lotate(K3); } //左-右型,先进行左旋,再右旋 static AvlNode L_R_Rotate(AvlNode K3) { //先对孩子进行左旋 K3.lchild = L_Rotate(K3.lchild); //在右旋 return R_Rotate(K3); } //插入数值操作 static AvlNode insert(int data, AvlNode T) { if (T == null) { T = new AvlNode(); T.data = data; T.lchild = T.rchild = null; } else if(data < T.data) { //向左孩子递归插入 T.lchild = insert(data, T.lchild); //进行调整操作 //如果左孩子的高度比右孩子大2 if (height(T.lchild) - height(T.rchild) == 2) { //左-左型 if (data < T.lchild.data) { T = R_Rotate(T); } else { //左-右型 T = L_R_Rotate(T); } } } else if (data > T.data) { T.rchild = insert(data, T.rchild); //进行调整 //右孩子比左孩子高度大2 if(height(T.rchild) - height(T.lchild) == 2) //右-右型 if (data > T.rchild.data) { T = R_Rotate(T); } else { T = R_L_Rotate(T); } } //否则,这个节点已经在书上存在了,我们什么也不做 //重新计算T的高度 T.height = Math.max(height(T.lchild), height(T.rchild)) + 1; return T; } }
AVL维护成本太高了,要求每个节点的左右子树高度差不能超过1。对于此,可以发现AVL的规则太严格了,为了微乎其微的查找速度,大大增加了插入速度。
此时红黑树就出现了。
红黑树
一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是red或black(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍。它是一种弱平衡二叉树(由于是弱平衡,可以推出,相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索、插入、删除操作较多的情况下,我们就用红黑树。
1、每个节点非红即黑;
2、根节点是黑的;
3、每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的;
4、如果一个节点是红的,那么它的两儿子都是黑的;
5、对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点;
6、高度始终保持在h = logn
7、红黑树的查找、插入、删除的时间复杂度最坏为O(log n)
节点插入:
新增的节点默认都是红色。理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。
但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多 1,必须做自平衡。
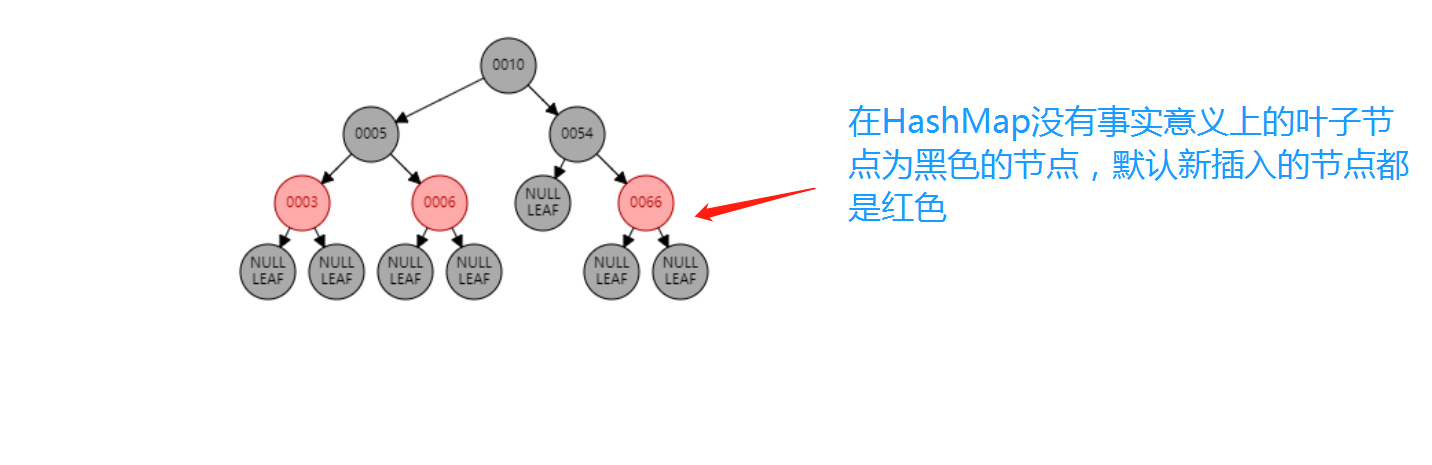
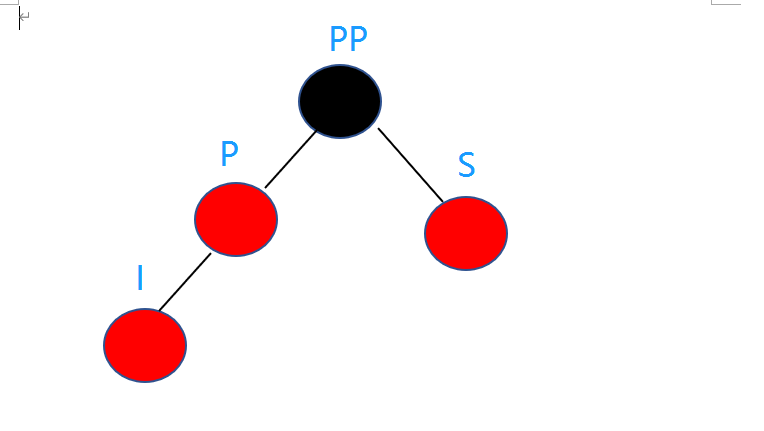
插入:
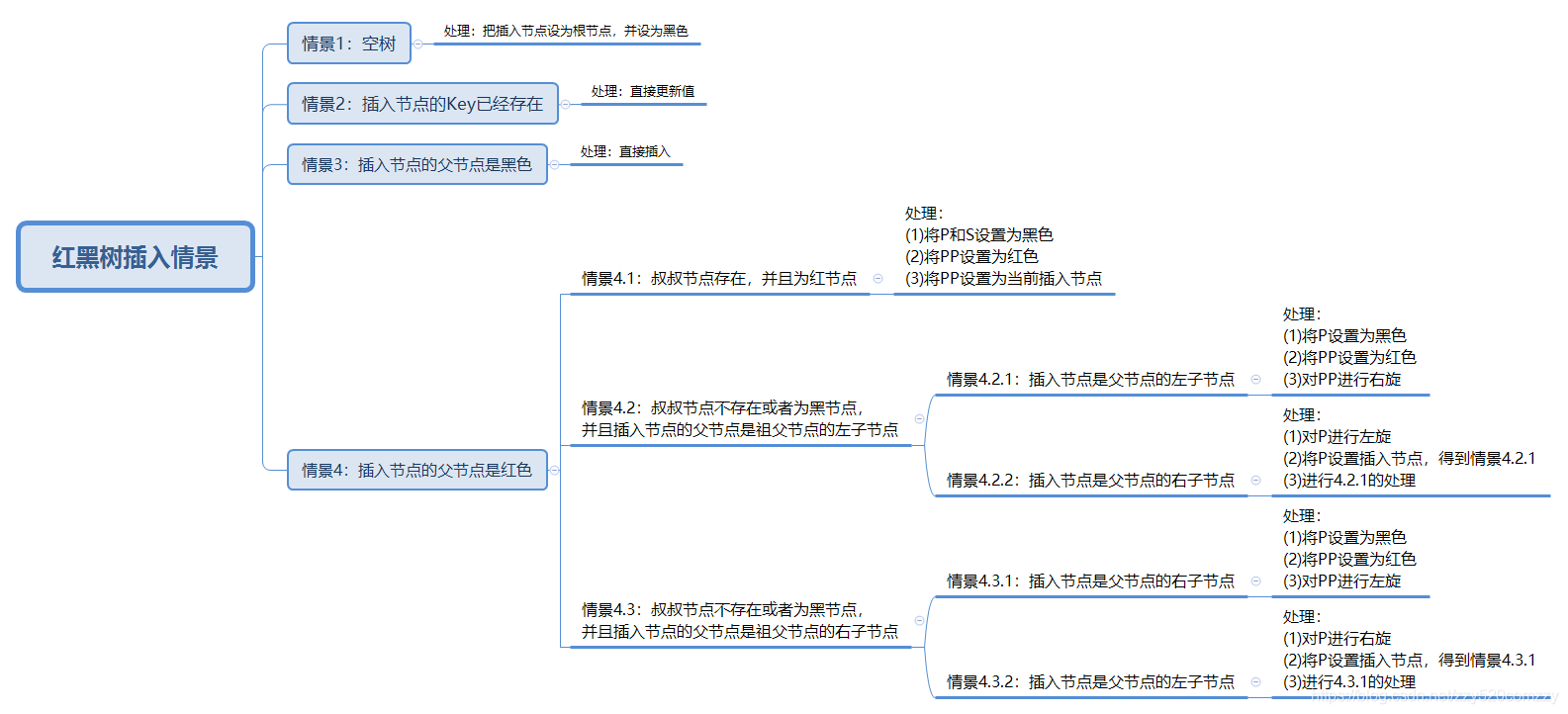
情景4:插入节点的父节点是红色。
情景 4.1:叔叔结点存在并且为红结点。
操作:将父节点5与叔叔节点15设置为黑色,祖父节点10设置为红色,因为祖父节点为根节点,故祖父节点改为黑色。
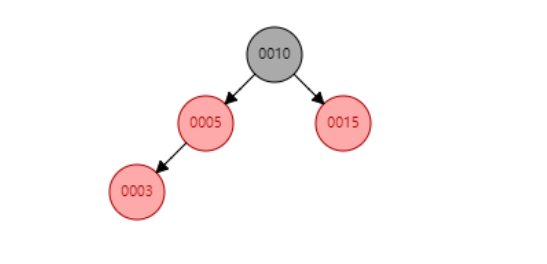
调整后:
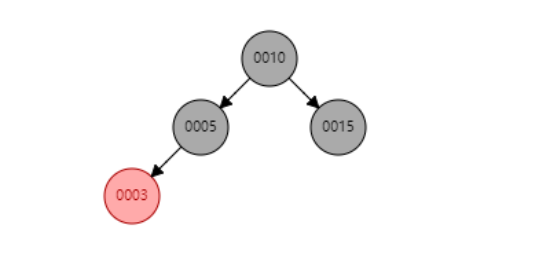
情景 4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点。
情景 4.2.1:插入结点是其父结点的左子结点。
操作:将父节点5设置为黑色,祖父节点设置为红色,对祖父节点进行右旋。
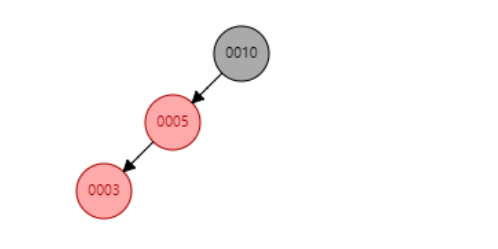
调整后:
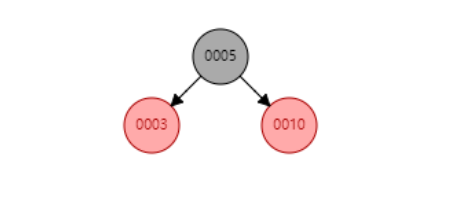
情景 4.2.2:插入结点是其父结点的右子结点。
操作:对父节点5进行左旋,得到情景4.2.1。

调整后:
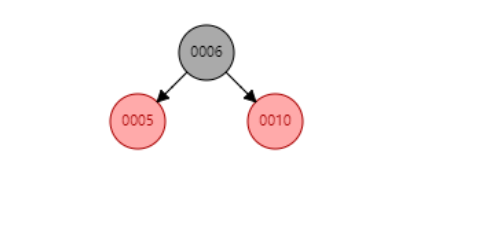
删除操作:
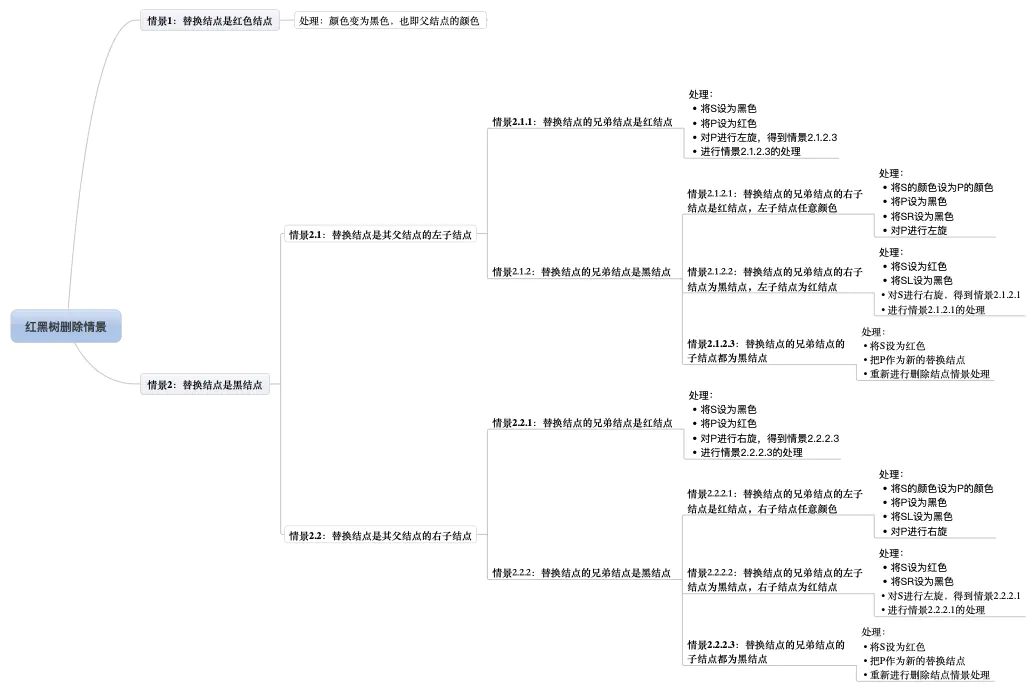
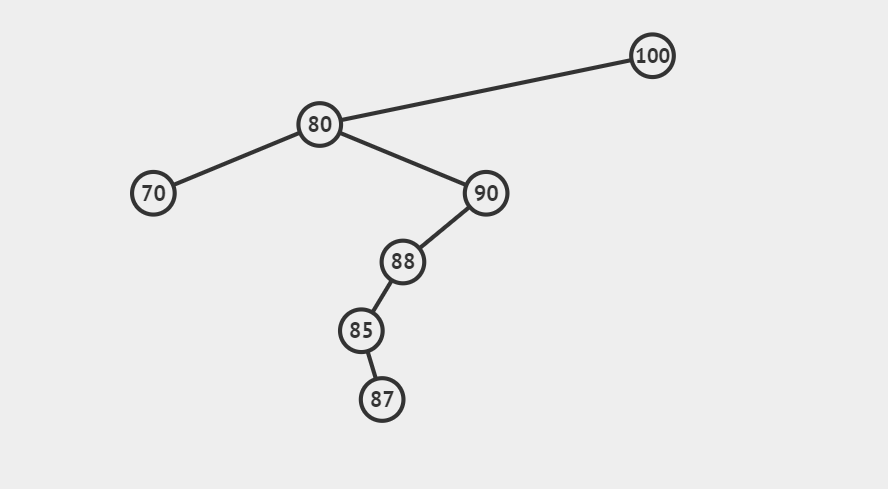
首先要找到目标节点、互换节点(删除节点)、替代节点
-
如果互换节点有子节点(互换节点 != 替代节点),先删除互换节点位置,把替代节点顶上来,再平衡。
-
如果互换节点没有子节点(互换节点 == 替代节点),先平衡,再删除
例如上图,删除节点80,那么目标节点是80,互换节点是85,替代节点是87。
二叉树目标结点找互换结点有3种情情景:
-
若目标结点无子结点,直接删除
-
若目标结点只有一个子结点,用子结点替换目标结点
-
若目标结点有两个子结点,用后继结点(大于目标结点的最小结点)替换目标结点
平衡的目的:让替换节点的树多一个黑节点或让父节点的另一颗子树少一颗黑节点。
-
删除结点是红色结点。
直接删除,用替换节点顶替,不需要走平衡调整。
如果删除节点p是叶子结点,那么直接删除即可,这样也不违反红黑树的5点性质;如果删除节点p是情景2的情况,那么直接用replacement顶替他即可,因为p是红色,直接删除了也不违背红黑树的5点性质。
-
删除节点是黑色
情景1:替代节点是红色:直接将颜色改黑色,让它所在的树的黑色节点加1,完成目标,返回
情景2:替换节点是黑色
情景2.1.1:替换结点的兄弟结点是红结点

SL必为红或者Nil
情景2.1.2.2:替换结点的兄弟结点的右子结点为黑结点,左子结点为红结点
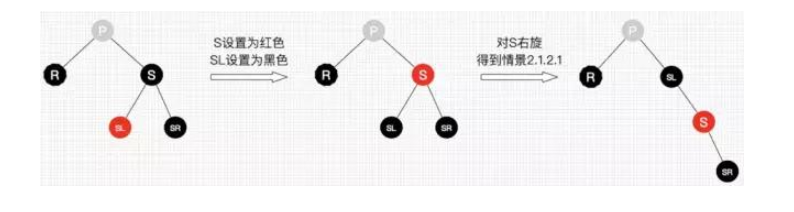
情景2.1.2.3:替换结点的兄弟结点的子结点都为黑结点

下次以P为节点,给P这颗树多一颗黑色。
插入代码:

/** * 红黑树节点平衡插入操作 * @param root 根节点 * @param x 插入节点 * @return 新root节点 */ static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { //首先插入节点x的颜色初始化为红色 x.red = true; //for循环没有结束条件,自底向上插入循环处理,直至到root或者红黑自平衡退出循环 for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { //如果xp为空,说明x已经为root了 if ((xp = x.parent) == null) { x.red = false; return x; } //否则判断父节点xp是否是黑色,或者xp是否为root else if (!xp.red || (xpp = xp.parent) == null) return root; //判断父节点xp是否是祖父节点的左孩子 if (xp == (xppl = xpp.left)) { //叔叔节点存在,并且为红节点 if ((xppr = xpp.right) != null && xppr.red) { //红黑树基础-第一篇,根据情景4.1进行变色 xppr.red = false; xp.red = false; xpp.red = true; //以xpp为插入节点,进行下一次循环 x = xpp; } //否则叔叔节点要么为空,要么为黑色 else { //如果插入节点x是父节点xp的右孩子,那么满足红黑树基础-第一篇,情景4.2.2 if (x == xp.right) { //把xp进行左旋,同时把插入节点x赋值为xp root = rotateLeft(root, x = xp); //重新设置xp和xpp xpp = (xp = x.parent) == null ? null : xp.parent; } //进行红黑树基础-第一篇,情景4.2.1的处理 if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; //xpp右旋 root = rotateRight(root, xpp); } } } } //否则父节点xp是祖父节点的右孩子 else { //叔叔节点存在,并且为红节点 if (xppl != null && xppl.red) { //红黑树基础-第一篇,根据情景4.1进行变色 xppl.red = false; xp.red = false; xpp.red = true; //以xpp为插入节点,进行下一次循环 x = xpp; } //否则叔叔节点要么为空,要么为黑色 else { //如果插入节点x是父节点xp的左孩子,那么满足红黑树基础-第一篇,情景4.3.2 if (x == xp.left) { //把xp进行右旋,同时把插入节点x赋值为xp root = rotateRight(root, x = xp); //重新设置xp和xpp xpp = (xp = x.parent) == null ? null : xp.parent; } //进行红黑树基础-第一篇,情景4.3.1的处理 if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; //xpp左旋 root = rotateLeft(root, xpp); } } } } } }
删除代码:
删除节点:

/** * Removes the given node, that must be present before this call. * This is messier than typical red-black deletion code because we * cannot swap the contents of an interior node with a leaf * successor that is pinned by "next" pointers that are accessible * independently during traversal. So instead we swap the tree * linkages. If the current tree appears to have too few nodes, * the bin is converted back to a plain bin. (The test triggers * somewhere between 2 and 6 nodes, depending on tree structure). * @param map 该hashmap * @param tab hashmap内部Node数组 * @param movable 是否需要移动root到链表头 * @param this 待删除节点p */ final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab, boolean movable) { int n; if (tab == null || (n = tab.length) == 0) return; int index = (n - 1) & hash; //root是根节点 TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl; //分别是this=p的链表指针的前驱和后继 TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev; if (pred == null) //如果要删除的p是链表的头,那么first = succ;并且tab[index] = succ; tab[index] = first = succ; else //否则链表断开this的链接 pred.next = succ; if (succ != null) //链表断开this的链接,把链表关系完善 succ.prev = pred; if (first == null) //空树 return; if (root.parent != null) //获取到真正的根root root = root.root(); if (root == null || root.right == null || (rl = root.left) == null || rl.left == null) { //根的左孩子的左孩子为空,基本上可以判断只剩2-6个node了,红黑树可以变成链表了 tab[index] = first.untreeify(map); // too small return; } TreeNode<K,V> p = this, pl = left, pr = right, replacement; //主要关注这种左右孩子都非空的场景,为什么这种这么复杂,请看我写的关于红黑树基础的其他博客 if (pl != null && pr != null) { //请看图解,我随便画了个图,节点名和变量名一致 TreeNode<K,V> s = pr, sl; //先找到大于删除节点p的最小节点,为什么这么做,请看红黑树基础-第3篇 while ((sl = s.left) != null) // find successor s = sl; //首先互换p节点和s节点的颜色,因为最终s要被换到p的位置,p要被换到s的位置 //互换后,在p位置的s因为是p的颜色,所以不影响红黑树的性质 //而换到s位置的p,颜色是原s节点的颜色 boolean c = s.red; s.red = p.red; p.red = c; // swap colors TreeNode<K,V> sr = s.right; TreeNode<K,V> pp = p.parent; if (s == pr) { // p was s's direct parent //此时s==sp==pr,其实是建立p和s的关系,将else的内容简化了 p.parent = s; s.right = p; } else { TreeNode<K,V> sp = s.parent; //建立p和sp的新父子关系,大家可以画图分析 if ((p.parent = sp) != null) { if (s == sp.left) sp.left = p; else sp.right = p; } //建立s和pr的新父子关系 if ((s.right = pr) != null) pr.parent = s; } p.left = null; //建立p和sr的新父子关系 if ((p.right = sr) != null) sr.parent = p; //建立s和pl的新父子关系 if ((s.left = pl) != null) pl.parent = s; //建立s和pp的新父子关系 //如果pp为空,之前p就是根节点,那么现在s就是根节点了 if ((s.parent = pp) == null) root = s; else if (p == pp.left) //如果原来p是pp的左孩子,互换后s就还是pp左孩子 pp.left = s; else pp.right = s; //如果sr不为空,则互换后p有右孩子,没有左孩子, if (sr != null) //单链接情况直接用孩子替换 replacement = sr; else //此时p没有孩子 replacement = p; } //单链接情况,单单只有左孩子 else if (pl != null) replacement = pl; //单链接情况,单单只有右孩子 else if (pr != null) replacement = pr; else //p是叶子结点 replacement = p; //互换后,如果p不是叶子结点,在树结构中直接把p节点干掉 if (replacement != p) { TreeNode<K,V> pp = replacement.parent = p.parent; if (pp == null) root = replacement; else if (p == pp.left) pp.left = replacement; else pp.right = replacement; p.left = p.right = p.parent = null; } //回到红黑树的平衡删除了,如果要删除的节点是红色,那么直接删除即可 //如果p是黑色的,那么此时就不满足红黑树的性质了,因为少了一个黑色节点,那么要进行balanceDeletion调整 //注意:p的颜色是原来s的颜色 TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement); //那么如果p是叶子结点,在树结构中直接把p节点干掉,detach断开连接 if (replacement == p) { // detach TreeNode<K,V> pp = p.parent; p.parent = null; if (pp != null) { if (p == pp.left) pp.left = null; else if (p == pp.right) pp.right = null; } } //是否需要把root放到链表head if (movable) moveRootToFront(tab, r); }
平衡节点代码:

/** * 平衡删除调整部分代码 * 情景?.?请见红黑树基础-第二篇-删除 这篇文章对应的解析 * @param x 替代节点 * @param root 树的根节点 * @return 调整后,新的root节点 * 变量规则,x是替代节点,xp是x的父节点,xpl是xp的左孩子,xpr是xp的右孩子 */ static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root, TreeNode<K,V> x) { for (TreeNode<K,V> xp, xpl, xpr;;) { //替代节点已经到达根节点,直接退出函数返回 if (x == null || x == root) return root; //如果x的父节点是空,说明x==root了 else if ((xp = x.parent) == null) { x.red = false; return x; } //如果替代节点是红色,直接变为黑色,返回 else if (x.red) { x.red = false; return root; } //情景2.1 else if ((xpl = xp.left) == x) { //情景2.1.1 if ((xpr = xp.right) != null && xpr.red) { xpr.red = false; xp.red = true; root = rotateLeft(root, xp); //此时,x不变,xp和xpr更新 xpr = (xp = x.parent) == null ? null : xp.right; } //如果xpr为空,那么右子树没有红节点借,找父母的兄弟去借吧,自底向上处理 if (xpr == null) x = xp; //否则,情景2.1.2,xpr是黑色 else { TreeNode<K,V> sl = xpr.left, sr = xpr.right; //如果xpr的左右孩子都是黑色,情景2.1.2.3 if ((sr == null || !sr.red) && (sl == null || !sl.red)) { //找父母的兄弟去处理,自底向上处理 xpr.red = true; x = xp; } else { //否则,左子树红色,右子树黑色 if (sr == null || !sr.red) { //情景2.1.2.2 if (sl != null) sl.red = false; xpr.red = true; root = rotateRight(root, xpr); //更新xpr和xp xpr = (xp = x.parent) == null ? null : xp.right; } //情景2.1.2.1 if (xpr != null) { xpr.red = (xp == null) ? false : xp.red; if ((sr = xpr.right) != null) sr.red = false; } //情景2.1.2.1 if (xp != null) { xp.red = false; root = rotateLeft(root, xp); } x = root; } } } //情景2.2 else { // symmetric //情景2.2.1 if (xpl != null && xpl.red) { xpl.red = false; xp.red = true; root = rotateRight(root, xp); //此时,x不变,xp和xpl更新 xpl = (xp = x.parent) == null ? null : xp.left; } //如果xpl为空,那么左子树没有红节点借,找父母的兄弟去借吧,自底向上处理 if (xpl == null) x = xp; //否则,情景2.2.2,xpl是黑色 else { //如果xpl的左右孩子都是黑色,情景2.2.2.3 TreeNode<K,V> sl = xpl.left, sr = xpl.right; if ((sl == null || !sl.red) && (sr == null || !sr.red)) { //找父母的兄弟去处理,自底向上处理 xpl.red = true; x = xp; } else { //否则,左子树黑色,右子树红色 if (sl == null || !sl.red) { //情景2.2.2.2 if (sr != null) sr.red = false; xpl.red = true; root = rotateLeft(root, xpl); //更新xpr和xp xpl = (xp = x.parent) == null ? null : xp.left; } //情景2.2.2.1 if (xpl != null) { xpl.red = (xp == null) ? false : xp.red; if ((sl = xpl.left) != null) sl.red = false; } //情景2.2.2.1 if (xp != null) { xp.red = false; root = rotateRight(root, xp); } x = root; } } } } }
AVL局限性:
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树。



