10.1 叉积 ，极角排序，扫描法求凸包

凸包：用一个凸多边形将所有点围起来，这个凸多边形就是凸包

 

1.先要引入一个数学工具，向量叉积

 

 

 

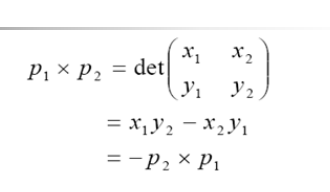
  |c|=|a×b|=|a| |b|sinα   （α为a，b向量之间的夹角）

则 |c| 为向量a ，b所组成的平行四边形的面积

这里是用叉积判断两向量的相对位置关系（非常有用！）

 

 

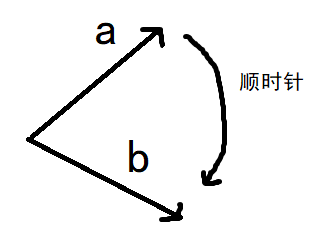
 则 a x b < 0 (a在b的逆时针方向 ） , b x a > 0（b在a的顺时针方向）

//求叉积
struct node{
    double x ,y;
    node operator -( const node & s ){
        return {x-s.x , y-s.y};
    }
}p[N] ,s[N];

inline double X( node a ,node b ){
    return a.x*b.y - b.x*a.y;
}

 

2. Graham扫描法求凸包

1）找出所有点中在最左下角的点定为极点

    //找左下边界点
     int k = 1;
     rep( i ,2 ,n ){
         if( p[i].y < p[k].y || p[i].y == p[k].y && p[i].x < p[k].x )
            k = i;
     }
     swap( p[1] ,p[k] );

 

2）利用叉积进行极角排序

//极角比较
bool cmp (  node &a , node &b ){
        double x = X(a-p[1] ,b-p[1]);
        //叉积判断向量位置关系
        if( x > 0 )return 1;
        if( x==0 && dis( a ,p[1])<dis( b ,p[1]) )return 1;
        return 0;
}

     //极角排序
     sort( p+2 ,p+n+1 ,cmp);

 

3）存凸包

s为存凸包的栈 ，t为栈顶

则由以下关系用叉积取舍s中的点

 

 

 

 

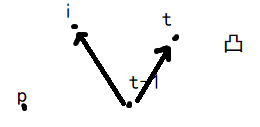
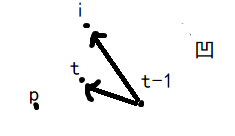
     //将凸包存在s中
     s[1] = p[1];
     s[2] = p[2];
     int t = 2;
     rep( i ,3 ,n ){
         while( t >= 2 && mul( s[t-1] ,s[t] ,p[i] )<=0 )t--;
         s[++t] = p[i];
     }

 

然后凸包就求出来了

 

模板题 ：

P2742 【模板】二维凸包 / [USACO5.1]圈奶牛

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <cstring>
#include <vector>
#include <map>
#include <unordered_map>
#define mem( a ,x ) memset( a , x ,sizeof(a) )
#define rep( i ,x ,y ) for( int i = x ; i<=y ;i++ )
#define lson l ,mid ,pos<<1
#define rson mid+1 ,r ,pos<<1|1
#define Fi first
#define Se second

using namespace std;
typedef long long ll ;
typedef pair<int ,int> pii;
typedef pair<ll ,int> pli;
const ll inf = 0x3f3f3f3f;
const int N = 1e5+5;
const ll mod = 1e9+7;

int n ,m;
//求叉积
struct node{
    double x ,y;
    node operator -( const node & s ){
        return {x-s.x , y-s.y};
    }
}p[N] ,s[N];

inline double X( node a ,node b ){
    return a.x*b.y - b.x*a.y;
}

inline double dis( node a ,node b ){
    return sqrt( (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

inline double mul( node a ,node b ,node c ){
    return X(b-a ,c-a);
}
//极角比较
bool cmp (  node &a , node &b ){
        double x = X(a-p[1] ,b-p[1]);
        //叉积判断向量位置关系
        if( x > 0 )return 1;
        if( x==0 && dis( a ,p[1])<dis( b ,p[1]) )return 1;
        return 0;
}

//Graham 扫描

int graham( ){
    //找左下边界点
     int k = 1;
     rep( i ,2 ,n ){
         if( p[i].y < p[k].y || p[i].y == p[k].y && p[i].x < p[k].x )
            k = i;
     }
     swap( p[1] ,p[k] );
     //极角排序
     sort( p+2 ,p+n+1 ,cmp);
     //将凸包存在s中
     s[1] = p[1];
     s[2] = p[2];
     int t = 2;
     rep( i ,3 ,n ){
         while( t >= 2 && mul( s[t-1] ,s[t] ,p[i] )<=0 )t--;
         s[++t] = p[i];
     }

     return t;
}

int main( ){
    scanf("%d" ,&n);
    rep( i ,1 ,n ){
        scanf("%lf%lf" ,&p[i].x ,&p[i].y );
    }
    int sz = graham( );
    
    double ans = dis(s[1] ,s[sz]);
    rep( i ,1 ,sz-1 )ans += dis( s[i] ,s[i+1] ) ;

    printf("%.2f" ,ans);
    return 0;
}