9.11 状态矩阵 与 dp
大一以来有两门课程学了矩阵：离散数学的二元关系一章的关系矩阵 和 线性代数中的矩阵
矩阵是一种特别方便的数学工具，线性代数中，它可以用来解线性方程组 ，而离散数学中，他可以描述一个由 二元关系的集合（可以看成是有向图） 所构成的状态；
而dp解决的是通过状态之间转移寻找最优解的问题。
所以当一个dp的状态由很多子状态构成 及 dp状态之间的转移较复杂 时，可以尝试用 关系矩阵 这个工具去描述它；
状态之间的转移，则用矩阵乘法去实现。
关于用矩阵乘法实现状态之间的转移，离散数学中有证明（关系矩阵的幂次，二元关系的复合），这里简单的说一下：
矩阵乘法的定义是这样的
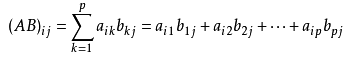
在关系矩阵中则可以表示两个二元关系的复合，为什么呢?
二元关系可以用有向图表示，用两个有向图 f ,g 复合为一个新的有向图 f * g，假设新的图中有一条边i -> j，则它是有f中的一条边i->k ，和 g 中的一条边 k->j通过一个中间节点k连接而成，而 矩阵乘法 恰好完成了枚举中间节点k这个过程，如下图
矩阵乘法行乘列这个过程，枚举了k = 1,2,3,4 这几个状态
例题：CF750E New Year and Old Subsequence
题意: 在区间$[l,r]$中删去最少的字符数使得在这个区间内不含有子序列$2016$且含有子序列$2017$如果无法满足条件,输出 -1
解析见：https://www.cnblogs.com/BCOI/p/10329108.html
和 区间dp 有点像 ， 先初始化每一点 i 的初始状态矩阵 fi ,可以看做有向图（i -> i），询问l -> r则通过线段树逐步完成 l -> r之间的转移（其实这里可以说是普通的二叉树，因为没用到线段树的关键：lazy 标记）
代码（The 2019 Asia Nanchang First Round Online Programming Contest -- c： hello 2019 ）：
#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <set> #include <queue> #include <stack> #include <string> #include <cstring> #include <vector> #define mem( a ,x ) memset( a , x ,sizeof(a) ) #define rep( i ,x ,y ) for( int i = x ; i<=y ;i++ ) #define lson l ,mid ,pos<<1 #define rson mid+1 ,r ,pos<<1|1 using namespace std; typedef long long ll ; typedef pair<int ,int> pii; typedef pair<ll ,int> pli; const int inf = 0x3f3f3f3f; const int N = 2e5+5; int n ,m; char s[N]; struct Mtx{ int a[5][5]; Mtx( ){ mem( a ,inf ); } }; Mtx updata( const Mtx & x, const Mtx & y ){
//状态之间的转移，矩阵乘法只是枚举k点的一种形式 ，实际并不是标准定义的矩阵乘法 Mtx tmp; rep( i ,0 ,4 ) rep( j ,0 ,4 ) rep(k ,0 ,4 ){ tmp.a[i][j] = min( tmp.a[i][j] ,x.a[i][k] + y.a[k][j] ); //cout<<i<<" "<<j<<tmp.a[i][j]<<endl; } return tmp; } struct Tree{ int l ,r ; Mtx m; }t[N<<2]; void pushup( int pos ){ t[pos].m = updata( t[pos<<1].m ,t[pos<<1|1].m ); } void build( int l ,int r ,int pos ){ t[pos].l = l , t[pos].r = r; int mid = (l+r>>1); if( l==r ){ rep( i ,0 ,4 ) t[pos].m.a[i][i] = 0; //最基本子的子状态的初始化 if(s[l] == '2') t[pos].m.a[0][0] = 1, t[pos].m.a[0][1] = 0; if(s[l] == '0') t[pos].m.a[1][1] = 1, t[pos].m.a[1][2] = 0; if(s[l] == '1') t[pos].m.a[2][2] = 1, t[pos].m.a[2][3] = 0; if(s[l] == '9') t[pos].m.a[3][3] = 1, t[pos].m.a[3][4] = 0; if(s[l] == '8') t[pos].m.a[3][3] = 1, t[pos].m.a[4][4] = 1; return; } build( lson ); build( rson ); pushup( pos ); } Mtx query( int pos ,int l ,int r ){ //cout<<" l ,r "<<l<<" "<<r<<endl; //cout<<t[pos].l<<" "<<t[pos].r<<endl; if( l <= t[pos].l && t[pos].r <=r )return t[pos].m; int mid = ( t[pos].l + t[pos].r )>>1; if( r <= mid ) return query( pos<<1 ,l ,r ); if( mid < l )return query( pos<<1|1 ,l ,r ); return updata( query( pos<<1 ,l ,r ) , query( pos<<1|1 ,l ,r ) ); } int main( ){ scanf("%d%d" ,&n ,&m ); scanf("%s" ,s+1 ); reverse( s+1 ,s+1+n ); // rep( i ,1 ,n )cout<<s[i]; //cout<<endl; build( 1 ,n ,1 ); while( m-- ){ int l ,r; scanf("%d%d" ,&r ,&l ); l = n+1-l; r = n+1 -r; Mtx ans = query( 1 ,l ,r ); printf( "%d\n" ,ans.a[0][4] == inf ? -1 : ans.a[0][4] ); } return 0; }
总结一下就是dp的状态可以看成一个有向图 ，然后通过关系矩阵连乘完成 一系列有向图的复合，也就是dp状态之间的转移
最关键部分是写出转移矩阵
