初等数论入门笔记
常见记号:
常见性质:
同余的性质
求gcd
1. 欧几里得算法
点击查看代码
inline int gcd( int a , int b ) { return b == 0 ? a : gcd( b , a % b ); }
2. stein算法(不需除法,适合高精)
线性同余方程
一元线性同余方程(扩展欧几里得算法;exgcd)
前置知识:
同余的性质、欧几里得算法
求解:
解任意同余方程
此时
※ 因此解同余方程
裴蜀定理:
-
表述:不定方程
-
简易证明:
∴
又∵
∴ -
推论:
扩展欧几里得算法(求解不定方程
Q: 为什么叫“扩展欧几里得算法”呢?
A: 因为这个算法在求出
由裴蜀定理可得:
若
记
因而先考虑求解
又由裴蜀定理知,此时存在
由欧几里得算法知
所以可联立上方两个式子:
整理,得:
要使上述式子恒成立,则
可以递归求解
递归边界和
解,得:当
点击查看代码
inline ll exgcd( ll a , ll b ) { if( b == 0 ) { x = 1; y = 0; return a;//递归边界同gcd一致,此时ax = gcd(a,0) = a , x = 1 } else { exgcd( b , a % b ); ll t = x;//储存x' x = y; y = t - ( a / b ) * y; } }
注意事项:大部分题目要求解出非负解,所以
推广应用(exgcd求乘法逆元)
逆元是什么,为什么要求逆元呢?
有些时候,在计数题中,我们要对有理数取模(取余)
例如计算
由分式的性质易得:
这也就是说,如果
--未完待续
线性同余方程组
筛法
1. 埃氏筛
2. 线性筛求素数
3. 线性筛求欧拉函数(求积性函数)
常见数论定理
1. 费马小定理
2. 欧拉定理
3. 中国剩余定理
本文作者:huasheng
本文链接:https://www.cnblogs.com/-hua-sheng-/p/16591748.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。


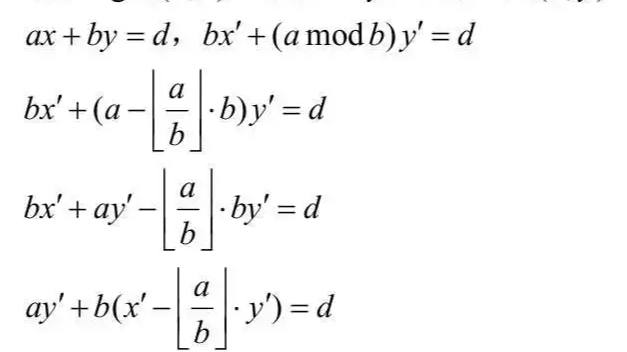 欧几里得算法,gcd
扩展欧几里得,exgcd
丢番图方程
费马小定理
欧拉定理
欧几里得算法,gcd
扩展欧几里得,exgcd
丢番图方程
费马小定理
欧拉定理



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步