bzoj2282 [Sdoi2011]消防

Description

某个国家有n个城市，这n个城市中任意两个都连通且有唯一一条路径，每条连通两个城市的道路的长度为zi(zi<=1000)。

这个国家的人对火焰有超越宇宙的热情，所以这个国家最兴旺的行业是消防业。由于政府对国民的热情忍无可忍（大量的消防经费开销）可是却又无可奈何（总统竞选的国民支持率），所以只能想尽方法提高消防能力。

现在这个国家的经费足以在一条边长度和不超过s的路径（两端都是城市）上建立消防枢纽，为了尽量提高枢纽的利用率，要求其他所有城市到这条路径的距离的最大值最小。

你受命监管这个项目，你当然需要知道应该把枢纽建立在什么位置上。

Input

输入包含n行：
第1行，两个正整数n和s，中间用一个空格隔开。其中n为城市的个数，s为路径长度的上界。设结点编号以此为1，2，……，n。
从第2行到第n行，每行给出3个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。例如，“2 4 7”表示连接结点2与4的边的长度为7。

 

Output

输出包含一个非负整数，即所有城市到选择的路径的最大值，当然这个最大值必须是所有方案中最小的。

Sample Input

【样例输入1】
5 2
1 2 5
2 3 2
2 4 4
2 5 3 



【样例输入2】
8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3

Sample Output

【样例输出1】

5
【样例输出2】

5

Hint

对于100%的数据，n<=300000，边长小等于1000。

Source

stage 2 day1

解法：

首先我们要知道以下几件事情：

1、枢纽一定在直径上。

2、如果有多条直径，每一条都是等效的，枢纽建在不同直径上对最长距离的最小值并没有影响。

3、直径的两个端点到枢纽的距离并不一定是最长的（我看有的大佬说错了）。

3（变式）、当整条直径都作为枢纽的时候，答案就变成了非直径上的点到直径的最长距离。

解释一下3：

对于以下这张图

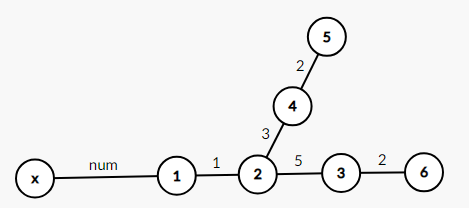
假设( x ,6)是树的直径，当前枢纽已经从 x 扩展到了2。对于2来说，离枢纽最远的点是6；但当枢纽扩展到3，离枢纽最远的点就是非直径的5。

知道这些后本题就很简单了。我们首先要找出一条直径，枚举上面的每一个点 u 作为枢纽的起点，然后向下扩展，找到满足条件最远的 v 。对于每一组（ u , v ）计算出直径的两个端点到 u 和 v 的距离，最后再对非直径上的点到直径的最远距离取一个 max 即可。

AC代码(略丑轻喷)：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

int n,s,num_edge,head[300008],dis[300008],maxx=-1,x,y,pre[300008],ans;

bool pd[300008];

struct Edge{
    int from,to,dis,next;
}edge[600008];

long long read()
{
    long long x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

void addedge(int from,int to,int dis)
{
    edge[++num_edge].next=head[from];
    edge[num_edge].from=from;
    edge[num_edge].to=to;
    edge[num_edge].dis=dis;
    head[from]=num_edge;
}

void dfs(int xx,int fa,int f)//寻找直径 
{
    for(int i=head[xx];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa) continue;
        if(f) pre[v]=xx;
        dis[v]=dis[xx]+edge[i].dis;
        dfs(v,xx,f);
    }
}

int find(int xx,int len)//判断核的大小 
{
    for(int i=head[xx];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==pre[xx]&&len>=edge[i].dis)
        {
            return find(v,len-edge[i].dis);
        }
    }
    return xx;
}

int work(int xx,int len)//寻找最长距离 
{
    int num1=dis[xx],po=find(xx,len);
    int num2=dis[x]-dis[po];
    return max(num1,num2);
}

void ask(int xx,int fa)//寻找其他点到直径上的最大距离 
{
    for(int i=head[xx];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(pd[v]) continue;
        if(v==fa) continue;
        dis[v]=dis[xx]+edge[i].dis;
        ask(v,xx);
    }
}

int main()
{
    n=read();s=read();
    for(int i=1;i<n;++i)
    {
        int a,b,c;
        a=read();b=read();c=read();
        addedge(a,b,c);
        addedge(b,a,c);
    }
    dfs(1,0,0);//寻找直径一点 
    for(int i=1;i<=n;++i)
        if(dis[i]>maxx)
        {
            x=i;
            maxx=dis[i];
        }
    maxx=-1;
    dis[x]=0;
    dfs(x,0,1);//寻找直径另一点 
    for(int i=1;i<=n;++i)
        if(dis[i]>maxx)
        {
            maxx=dis[i];
            y=i;
        }
    memset(dis,0,sizeof(dis));
    int now=y;
    dis[now]=0;
    pd[now]=1;
    while(now!=x)//处理直径上每一个点到y的距离 
    {
        for(int j=head[now];j;j=edge[j].next)
        {
            int v=edge[j].to;
            if(v==pre[now])
            {
                pd[v]=1;
                dis[v]=dis[now]+edge[j].dis;
            }
        }
        now=pre[now];
    }
    now=y;
    int ans=1e9;
    while(now!=x)//处理直径端点的距离
    {
        ans=min(ans,work(now,s));
        now=pre[now];
    }
    ans=min(ans,work(x,s));
    memset(dis,0,sizeof(dis));
    now=y;
    while(now!=x)//处理其他点到直径的距离 
    {
        ask(now,0);
        now=pre[now];
    }
    ask(x,0);
    for(int i=1;i<=n;++i)
        ans=max(ans,dis[i]);
    printf("%d",ans);
    return 0;
}

 

最后偷偷告诉你们，其实这道题每一个数据的 s 都大于直径的总长度，问题就变成了寻找非直径上的点到直径的最远距离了，两个 dfs 就可以解决。