算法作业12——图的 m 着色问题

1. 问题

图的 m 着色问题。给定无向连通图 G 和 m 种颜色，用这些颜色给图的顶点着色，每个顶点一种颜色。如果要求 G 的每条边的两个顶点着不同颜色。给出所有可能的着色方案；如果不存在，则回答“NO”。

 

2. 解析

设 G 有 n 个顶点，将顶点编号为1 ,2 ,... ,n ,则搜索空间为深度n的m 叉完全树，将颜色编号为1 , 2 ,... ,m ,结点<x₁ ,x₂ ,... ,x_k>(x₁ ,x₂ ,... ,x_k ϵ{1, ... ,m},1 ≤ k ≤ n)表示顶点1的颜色x₁ ,顶点2的颜色x₂ ,... ,顶点k的颜色x_k .

 

实例：4顶点，4颜色

四叉树：

 

 

 

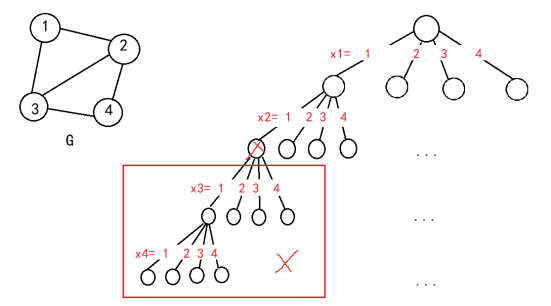
3. 设计

n //顶点数

m //颜色数

c[MAX][MAX] //邻接矩阵，0、1表示两点之间是否连通

color[MAX] //初始值0,1-m代表颜色

Flag=0 //初始表示不存在填色方法

1. 输入n,m,c[]
2. OK

If点相邻且颜色相同then return false

Else return true

1. FillColor

(1) 初始化color[]为0，表示尚未填色

(2) While：遍历n层：

While： If 第k种颜色<=m 且连通 then return break

Else 下一种颜色

If(color[k]<=m&&k==n) then 输出该种填色方法,flag=1

Else if(color[k]<=m&&k<n) then k++,向下遍历

Else color[k]=0,k--,回溯

 

If flag=0 then 输出NO

 

 

 

4. 分析

m是颜色数，n是顶点数

结点数=

 

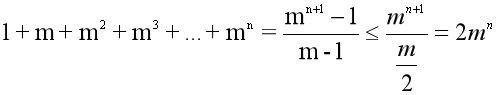
每个结点和其他结点进行n-1次比较

 

5. 源码

https://github.com/2579081436/algorithm.github.io