算法作业8——矩阵链的乘法

1. 问题

设A₁,A₂,A₃,…,A_n为 n 个矩阵的序列，其中A_i为P_i-1*P_i阶矩阵，这个矩阵链的输入用向量P=<P₀,P₁,…,P_n>给出。
给定向量 P，确定一种乘法次序，使得基本运算的总次数达到最小。

2. 解析

蛮力法

枚举所有可能的乘法次序，针对每种次序计算基本运算的次数，从中找出具有最小运算次数的乘法次序，每一种乘法次序对应了一种 在n个项中加n-1对括号。

动态规划法

A_i..j表示矩阵链相乘的子问题A_iA_i+1...A_j；

m[i..j] 表示得到乘积A_i..j所用的最少基本运算次数；

 

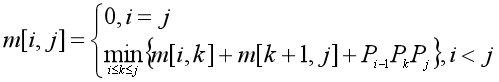
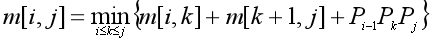满足优化原则,即m[i,j]最小值时,m[i,k]和m[k+1,j]也是最小的。

 

 

实例：P=<30,35,15,25,10,5>,n=5

 

A₁=30*35

 

A₂=35*15

 

A₃=15*25

 

A₄=25*10

 

A₅=10*5

 

 

 

（1）r=1

 

m[1,1]=0

 

m[2,2]=0

 

m[3,3]=0

 

m[4,4]=0

 

m[5,5]=0

 

（2）r=2,i=1,2,3,4 ;j=2,3,4,5

 

m[1,2]=30*35*15=15750

 

m[2,3]=35*15*25=13125

 

m[3,4]=15*25*10=3750

 

m[4,5]=25*10*5=1250

 

（3）r=3,i=1,2,3 ;j=3,4,5

 

m[1,3]=min{m[1,2]+m[3,3]+(A₁A₂)A₃, m[1,1]+ m[2,3]+A₁(A₂A₃)}

 

m[2,4]=min{m[2,3]+m[4,4]+(A₂A₃)A₄, m[2,2]+ m[3,4]+A₂(A₃A₄)}

 

m[3,5]=min{m[3,4]+m[5,5]+(A₃A₄)A₅, m[3,3]+ m[4,5]+A₁(A₂A₃)}

 

（4）r=4,i=1,2 ;j=4,5

 

m[1,4]=min{ m[1,1]+ m[2,4]+A₁(A₂A₃A₄), m[1,2]+ m[3,4]+(A₁A₂)(A₃A₄),m[1,3]+ m[4,4]+(A₁A₂A₃)A₄};

 

m[2,5]=min{ m[2,2]+ m[3,5]+A₂(A₃A₄A₅), m[2,3]+ m[4,5]+(A₂A₃)(A₄A₅),m[2,4]+ m[5,5]+(A₂A₃A₄)A₅};

 

（5）r=5,i=1 ;j=5

 

m[1,5]=min{m[1,1]+m[2,5]+A₁(A₂A₃A₄A₅),m[1,2]+m[3,5]+(A₁A₂)(A₃A₄A₅),m[1,3]+m[4,5]+(A₁A₂A₃)(A₄A₅),m[1,4]+ m[5,5]+ (A₁A₂A₃A₄)A₅};

 

3. 设计

Define max=1000000

MatrixChain(P,n)

输入：矩阵链A_i...j的输入向量P=<P_i-1,P_i,...,P_j> 1<=i<=j<=n

输出：计算A_i...j所需最小乘法运算次数m[i..j]和最后一次运算的位置s[i..j]

1. 令所有 m[i,j]初值为 0，s[i,j]的初值为 i，1<=i<=j<=n
2. For r=2 to n do //r 为当前问题规模（长度）
3. For i=1 to n-r+1 do //i 的起点不断变化，各种 r 长
4. j=i+r-1 //不同终点
5. m[i,j]=m[i+1,j]+max
6. For k=i+1 to j-1 do   //不同的划分位置
7. t=m[i,k]+m[k+1,j]+P_i-1P_kP_j
8. If t<m[i,j]
9. Then m[i,j]=t,s[i,j]=k

4. 分析

T(n)=O(n³)

5. 源码

https://github.com/2579081436/algorithm.github.io