算法作业9-1——最长公共子序列问题
1. 问题
给定序列
X=<x1,x2,...,xm>
Y=<y1,y2,...,yn>
求 X 和 Y 的最长公共子序列Z
2. 解析
Xi=<x1,x2,...,xi>
Yj=<y1,y2,...,yj>
Zk=<z1,z2,...,zk>
如果Zk是Xi和Yj的最长公共子序列
（1） xi=yj，那么zk=xi=yj，Zk-1是xi-1和Yj-1的最长公共子序列
（2） xi<>yj，zk<>xi，那么Zk是Xi-1和Yj的最长公共子序列
（3） xi<>yj，zk<>yj，那么Zk是Xi和Yj-1的最长公共子序列
递推关系：
C[i,j]表示是Xi和Yj的最长公共子序列（Zk）长度
i是X长度；j是Y的长度
实例：
3. 设计
算法1：给出最长子串长度
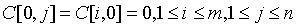
For i=1 to m
For j=1 to n
算法2：f(B,i,j)输出最长子串
If i=0 or j=0
then return 空串；
If B[i,j]=←
then 输出xi,且删除xi,删除yj
Else if B[i,j]=↑
then return f(B,i-1,j) //删除xi
Else
return f(B,i,j-1) //删除yj
4. 分析
T=O(mn),
m是X序列长度，n是Y序列长度
