算法作业6——选第k小的元素：特定分治策略

1. 问题

设L是n个元素的集合，从L中选取第k小的元素，其中1<=k<=n.这里的第k小元素是指，当L按从小到大排好序之后，排在第k个位置的元素。

2. 解析

 

 

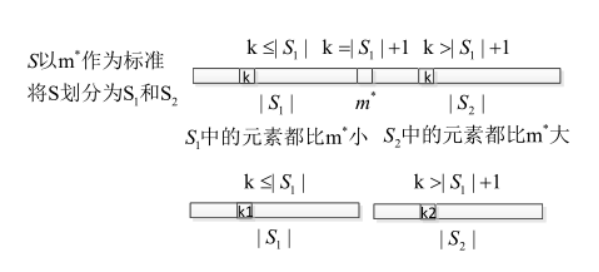
①k=|S₁|+1,m^*就是所要找的第k小的数；（以m^*为划分标准后，比m^*小的有|S₁|个,如果恰巧k=|S₁|+1,则m^* 就是所要找的第k小的数）

②k <=|S₁|，归约为在S₁中找第 k₁小的子问题，k₁在子问题中相对位置不变，即 k₁=k；

③k >|S₁|+1 ，归约为在S₂中找k₂位置的子问题，k₂ 相对于S₂子问题和 k 相对于S的关系，即 k₂= k-|S₁|-1。（在S中找k,就是在S₂中找k₂）

3. 设计

Select(S,k)

①将数组S中的元素每5个分为一组，共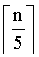组；

 

 

 

②对每个组的5个元素从大到小排序；

 

 

 

③将所有排好序后的数组中的中位数放到一个集合；

④从该集合中找到中位数m*,将S中元素分为4块：A、B、C、D，B已在S2中，C在S1中，把A、D中的每个元素和m*对比，小于m*放入S1，大于m*放入S2

⑤如果k=|S1|+1,则输出m*,如果k<=|S1|,则Select(S1,k)，否则，Select(S2,k-|S1|-1)

 

 

 

 

 

 

 

 

4. 分析

如果 A 和 D 的所有元素都小于 m*，那么它们的元素都加入 S1，且下一步算法又 在这个大的子问题 上进行递归调用，这对应了归约后子问题规模的上界，算法复杂度的最坏情况。

|A|+|D|+|C|=2r+2r+(3r+2)=7r+2=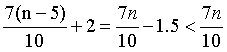

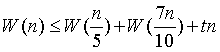
其中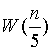，为查找 m*的时间，总规模 n 中选出 n/5 个数来找中位数tn是构造中位数集合，以及A &D和m*进行比较的时间开销，t是某个常数

 

 

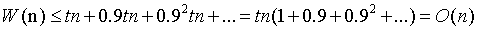
5. 源码

https://github.com/2579081436/algorithm.github.io