算法作业5——分治法求最近点对问题

1. 问题

在一个平面上，有n个点，每两个点称作一个点对，在所有点对中，求解出其中最小点对距离。

 

2. 解析

 

 

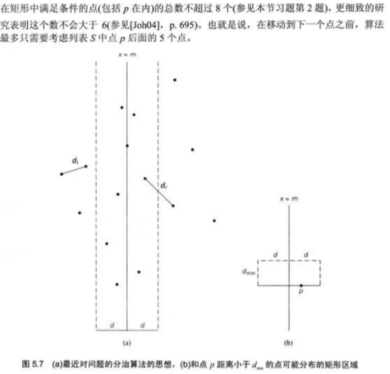
3. 设计

struct Node {
    double x, y;//X轴坐标，Y轴坐标
    
    //优先以X轴坐标升序，依次以Y轴坐标升序
    friend bool operator < (const Node& a, const Node& b) {
        if (a.x == b.x)
            return a.y < b.y;
        return a.x < b.x;
    }
};

//求两点之间的直线距离
double distance(const Node a, const Node b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
//从两个距离中，返回较小的
double Smaller(double d1, double d2)
{
    return (d1 > d2) ? d2 : d1;
}

//核心
double Closest_distance(int left, int right)
{
    double d = INF;//默认无穷大
    double distance_tmp;
    //只有一个点，最小距离即为0
    if (left == right)  return 0;

    //只有两个点，最小距离即为两点直线距离
    if (right - left == 1)  return distance(Point[left], Point[right]);

    //三个点以上
    int mid = (left + right) / 2;
    d = Smaller(Closest_distance(left, mid), Closest_distance(mid, right));

    for (int i = mid - 1; i >= left && Point[mid].x - Point[i].x < d; i--) {
        for (int j = mid + 1; j <= right && Point[j].x - Point[mid].x < d && fabs(Point[i].y - Point[j].y) < d; j++) {
            distance_tmp = distance(Point[i], Point[j]);
            if (distance_tmp < d)
                d = distance_tmp;
        }
    }

    return d;
}

 

4. 分析

 

 

5. 源码

https://github.com/2579081436/algorithm.github.io