算法作业1——Prim和Kruskal算法

1.问题

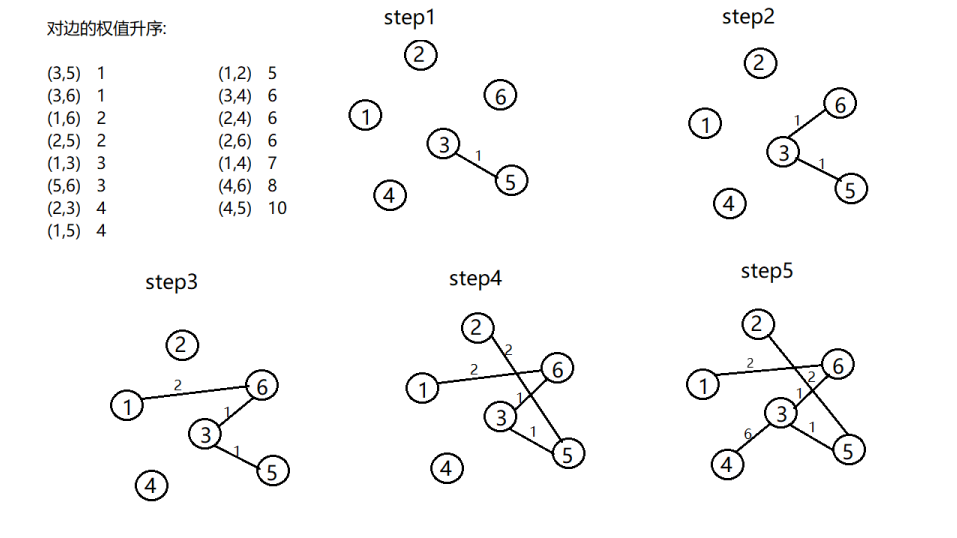
　　　　给定一个带权图G(V,E)，使用Kruskal和Prim算法得出该图的最小生成树和最小权值和。

2.解析

 

 

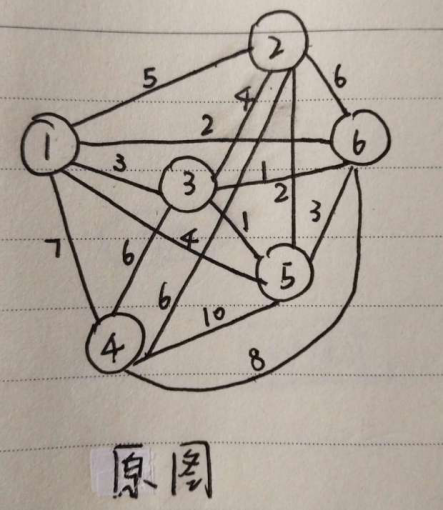
Prim构树过程

 

 

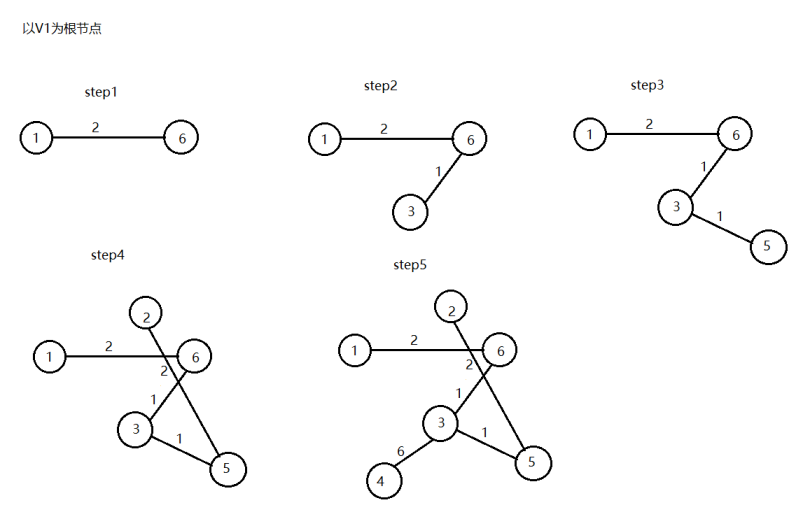
Kruskal构树过程

 

 3.设计

Kruskal伪代码：

并查集
找根节点
连接两个根节点

初始化G(v,e)  d{起点，终点，权值}

据权值，对d升序
count <- 点数
ans <- 0
for i:0 to m
if 某两个点连通 then
ans:=ans+某两点的边长
count:=count-1 
end
if count=1 then 输出最小权值和
else 没有最小生成树





Prim伪代码：
初始化距离w[][]为无穷大INF

for i:1 to n
    if 1到i点连通 then 根节点是1
距离d是1到i点的距离
end
While true do
初始化最小权值和min <- INF
k <- -1
for i:1 to n 
if 根节点到i点的最小权值和未确定then
min更新为的d[i]
k <- i
end
if  then 退出循环
根节点到i点的最小权值和确定 visited更新1
for i:1 to n
        if 根节点到i点的最小权值和未确定且当前的最小距离小于k到i的距离 then
d更新成k到i的距离
点i的根节点是k
end
end
整个图的最小权值和ans<-0
for i:1 to n
if 某个点没有遍历过 then 不存在最小生成树
else ans：ans+d
end
    输出最小生权值和

4.分析

Kruskal:T(n)=O(elog₂e)

Prim:T(n)=O(n²)

5.源码

https://github.com/2579081436/algorithm.github.io