浅谈基数排序

woc,学完发现自己貌似之前会？？？

这里简单介绍一下基数排序。(这是一个稳定的排序哦)

基数排序是桶排序的扩展具体怎么扩展我也不知道.

基本思想：

　　把整数按位切割成不同的数字,然后按每个位数分别比较。

具体做法：

　　把所有数的数位统一,高位没有的补零。

　　　然后从低位到高位,对每一位进行一次排序。这里不是用sort(#`O′)！

这里直接给出栗子：

{\(102,237,70,167,228,12,202,63,146,92\)}.

然后首先要变成这个样子.

{\(102,237,070,167,228,012,202,063,146,092\)}

具体的流程如下：(这里我比较习惯竖着写咯.)

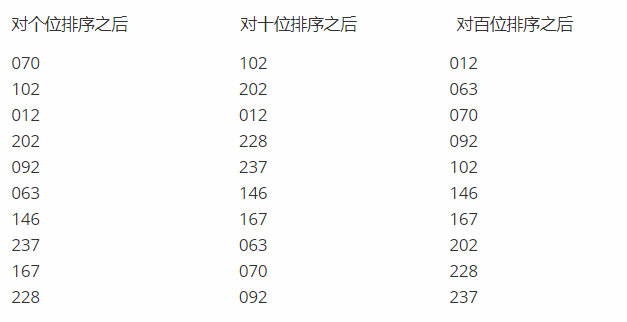
这个思想是不是超级好懂？

但是！如果我们对每一次都无序地对这些数排列的话,显然不能得到一个有序的序列。

因此我们基数排序最后需要倒着放回去。(这样能保证稳定性但我不会证明QAQ)

复杂度分析：

时间复杂度

很明显,我们需要排序的次数取决于最多是几位数.

即时间复杂度为\(O(n \times maxdigit )\)

空间复杂度

我们只需要一个临时数组来记录新位置上的数是谁,并记录每一位上的每个数的出现次数即可。

因此,空间复杂度为\(O(n)\)

代码：

剩下的就不多说了,直接放代码就好了.

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define R register

using namespace std;

const int gz=1e5+8;

inline void in(R int &x)
{
	R int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}

int n,a[gz],tmp[gz],cont[10];

inline int get()//求最大位数
{
	R int d=1,p=10;
	for(R int i=1;i<=n;i++)
		while(a[i]>=p)
			p*=10,d++;
	return d;
}

inline void radixsort()//基数排序
{
	R int d=get(),p=1;
	for(R int i=1;i<=d;i++,p*=10)//进行d次排序
	{
		memset(cont,0,sizeof cont);//每次清空计数器。
		for(R int j=1;j<=n;j++)
		{
			R int now=(a[j]/p)%10;//取出当前位上的数
			cont[now]++;//记录0~9每个数的出现次数.
		}
		for(R int j=1;j<10;j++)
			cont[j]+=cont[j-1];//求前缀和.
		for(R int j=n;j;j--)//倒放,保证顺序.
		{
			R int now=(a[j]/p)%10;
			tmp[cont[now]]=a[j];//放进临时数组.
			cont[now]--;//这个数的出现次数减一.
		}
		for(R int j=1;j<=n;j++)
			a[j]=tmp[j];//将临时数组赋给a数组.
	}
}

int main()
{
	in(n);
	for(R int i=1;i<=n;i++)in(a[i]);
	radixsort();
	for(R int i=1;i<=n;i++)
		printf("%d ",a[i]);
}