数字组合转字母|删除二叉树节点|字符串相乘|打家劫舍ii-无序数组第k大 |无序数组前k大|两个有序数组合并|中文数字转换为整数|最大连续子数组和|零钱凑数|两个有序数组寻找第k大的数
一、数字串转换为字符串
1-26个数字分别代表26个字符(A-z)输入"12326〞就可以拆分为【1,2,3,2，6】、(12, 3, 2, 6]. [1, 23, 2, 6]【1,23,26】、【12，3,26】等，将每种组合转成成对应字母输出，输出所有可能的结果
返回所有可能的转换结果
// 将数字串转换成字母串
// 将数字串转换成字母串 func numToStr(s string) []string { var result []string var path []byte // 用于存储当前路径 backtrack(s, 0, &result, path) return result } func backtrack(s string, index int, result *[]string, path []byte) { if index == len(s) { // 如果到达了字符串末尾，将当前路径添加到结果中 *result = append(*result, string(path)) return } // 一位数情况 if index < len(s) { num1 := s[index] - '0' // 转换为数字 if num1 >= 1 && num1 <= 9 { // 确保是有效的字母 (1-9) path = append(path, byte('A'+num1-1)) // 将数字转为对应字母 backtrack(s, index+1, result, path) // 继续递归 path = path[:len(path)-1] // 回溯 } } // 两位数情况 if index+1 < len(s) { num2 := (s[index]-'0')*10 + (s[index+1] - '0') // 转换为二位数字 if num2 >= 10 && num2 <= 26 { // 确保是有效的字母 (10-26) path = append(path, byte('A'+num2-1)) // 将数字转为对应字母 backtrack(s, index+2, result, path) // 继续递归 path = path[:len(path)-1] // 回溯 } } }
二、删除搜索二叉树的指定节点
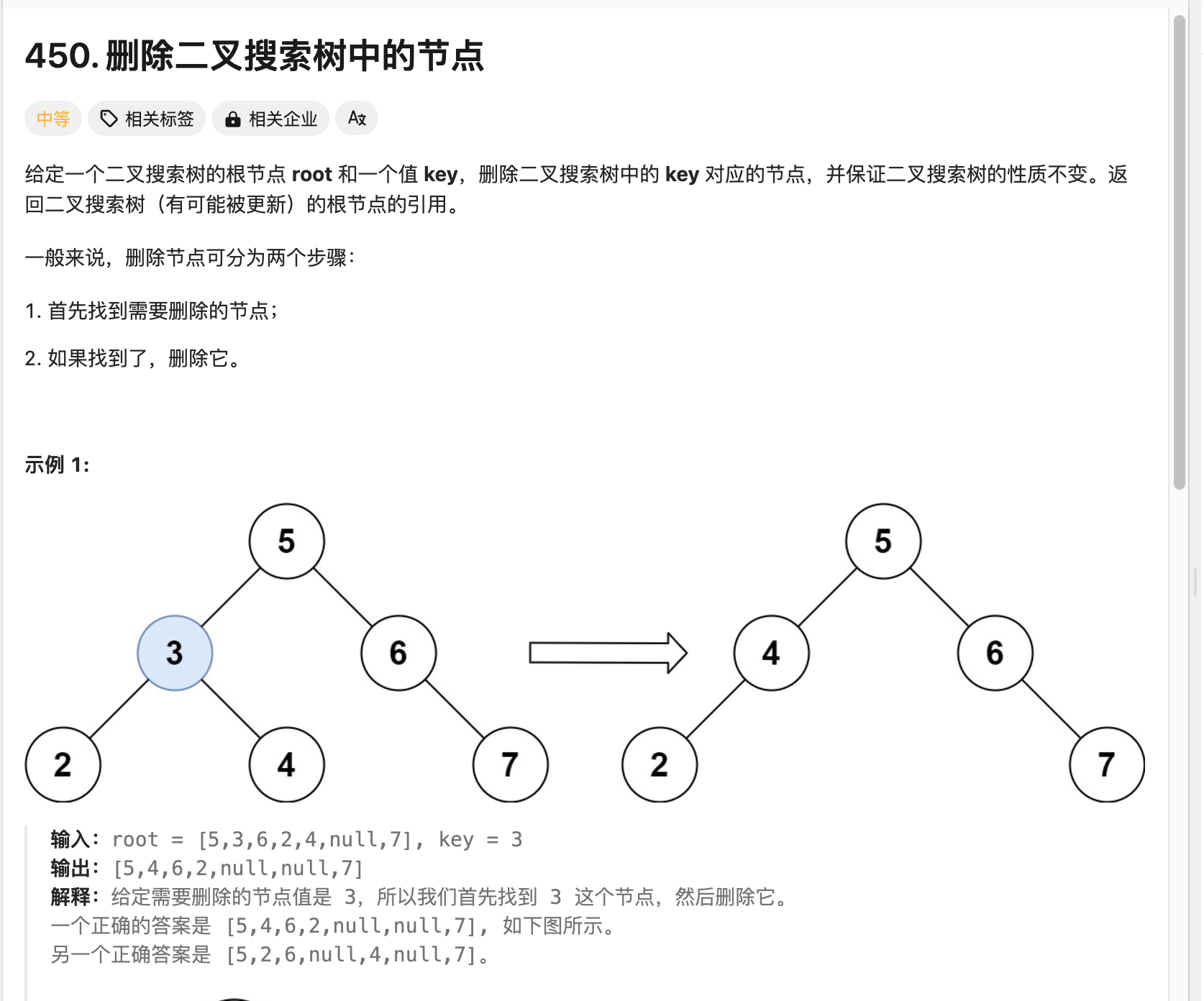
解题思路
当前节点比删除值小，右子树的根变为右子树中删除；
当前节点比删除值大，左子树的根变为左子树中删除；
当前就是要被删的节点，如果它没有左子树或没有右子树，可以直接平移嫁接。
否则需要找到左子树最大值或右子树最小值作为新的根。
链接： https://leetcode.cn/problems/delete-node-in-a-bst/solutions/1531382/-by-himymben-7sey/
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func deleteNode(root *TreeNode, key int) *TreeNode { if root != nil { if root.Val < key { root.Right = deleteNode(root.Right, key) } else if root.Val > key { root.Left = deleteNode(root.Left, key) } else { if root.Left == nil || root.Right == nil { if root.Left != nil { root = root.Left } else { root = root.Right } } else { node := root.Left for node.Right != nil { node = node.Right } node.Left = deleteNode(root.Left, node.Val) node.Right = root.Right root = node } } } return root }
三、字符串数字相乘
题目：给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。
num1和num2的长度小于110。num1和num2只包含数字0-9。num1和num2均不以零开头，除非是数字 0 本身。- 不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理
基于竖式乘法，先逐位乘算，再进位相加：
func multiply(num1 string, num2 string) string { // 有0参与直接返回0 if num1 == "0" || num2 == "0" { return "0" } // 某个为1直接返回另一个 if num1 == "1" { return num2 } if num2 == "1" { return num1 } // 定义map用于暂存每一位的临时结果 tmp := map[int]rune{} // 按照逐位相乘，错位相加的思想，遍历计算 i := 0 for _, a := range num1 { j := 0 for _, b := range num2 { tmp[i+j] += (a - 48) * (b - 48) j++ } i++ } var ( c rune res string ) // 逐位相加后连接字符串 for i := len(tmp) - 1; i >= 0; i-- { tmp[i] += c c = tmp[i] / 10 res = string([]rune{tmp[i]%10 + 48}) + res } // 将最后一个进位连接上 if c != 0 { res = string([]rune{c + 48}) + res } return res }
链接： https://segmentfault.com/a/1190000021756333?utm_source=tag-newest
四、打家劫舍ii
func rob(nums []int) int { n := len(nums) //细分情况 dp0, dp1 := [2]int{0, 0}, [2]int{0, nums[0]} if n < 2{ // 仅有一个元素的特殊情况，容易遗漏 return dp1[1] } // 照搬dp 方程 for i := 1; i < n; i++{ dp0[0], dp0[1] = max(dp0[0], dp0[1]), dp0[0] + nums[i] dp1[0], dp1[1] = max(dp1[0], dp1[1]), dp1[0] + nums[i] } return max(dp0[0], dp0[1], dp1[0]) } func max(nums ...int)int{ m := nums[0] for _, c := range nums{ if m < c{ m = c } } return m }
五、无序数组第k大
#include <iostream> #include <cstring> using namespace std; int func(int *arr, int l, int r, int k) { if (k-1 < l || k-1 > r) { return -1; } int p = l; int key = arr[r]; for (int i = l; i < r; ++i) { if (arr[i] > key) { int tmp = arr[p]; arr[p] = arr[i]; arr[i] = tmp; p++; } } if (p == k-1) { return key; } else if (p > k-1) { return func(arr, l, p-1, k); } else { arr[r] = arr[p]; return func(arr, p+1, r, k); } } int main() { int arr[] = {12,43,56,7,90,7,0,8,58,32,21}; int len = sizeof(arr) / sizeof(int); int *tmp = new int[len]; for (int i = -1; i <= len+1; ++i) { memcpy(tmp, arr, sizeof(arr)); cout << func(tmp, 0, len-1, i) << ' '; } delete[] tmp; return 0; }
链接： https://www.cnblogs.com/zuofaqi/p/10209648.html
七、无序数组前k大 快排实现
这个算法的基本思想是基于快速排序，它通过选取一个“基准”元素，将数组分成两个部分：小于基准的和大于基准的。然后根据需要的个数决定继续在哪一部分进行查找。
package main import ( "fmt" "math/rand" ) // partition将数组分为两部分，小于等于pivot的放到左侧，大于pivot的放到右侧 func partition(arr []int, left, right, pivotIndex int) int { pivotValue := arr[pivotIndex] // Swap pivot with the rightmost element arr[pivotIndex], arr[right] = arr[right], arr[pivotIndex] storeIndex := left for i := left; i < right; i++ { if arr[i] > pivotValue { // 找前k大的，所以是大于 arr[storeIndex], arr[i] = arr[i], arr[storeIndex] storeIndex++ } } // Move pivot to its final place arr[right], arr[storeIndex] = arr[storeIndex], arr[right] return storeIndex } // quickSelect返回数组中前k大的元素 func quickSelect(arr []int, left, right, k int) []int { if left <= right { // Randomly select a pivot index pivotIndex := left + rand.Intn(right-left+1) pivotIndex = partition(arr, left, right, pivotIndex) // Check the position of the pivot if pivotIndex == k { return arr[:k] } else if pivotIndex < k { return quickSelect(arr, pivotIndex+1, right, k) } else { return quickSelect(arr, left, pivotIndex-1, k) } } return nil } // FindTopK 返回无序数组中的前k大元素 func FindTopK(arr []int, k int) []int { if k <= 0 || k > len(arr) { return nil } return quickSelect(arr, 0, len(arr)-1, k) } func main() { arr := []int{3, 2, 1, 5, 6, 4} k := 2 topK := FindTopK(arr, k) fmt.Println(topK) // 输出前k大的元素 }
八、两个有序数组合并
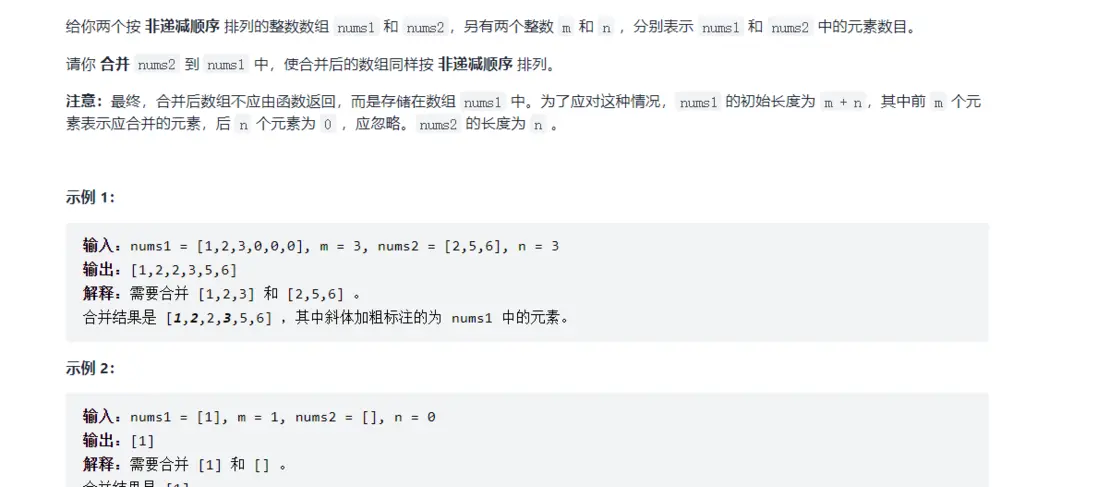
由题可知，我们需要将第二个数组的元素合并到第一个数组之后返回
两个数组都是有序的，因此对于每个想要插入数组的元素，我们只要找到首个大于这个元素的数，将其插入到这个数的前方即可
复杂度分析
时间复杂度：O（m+n）执行的循环次数为数组二的个数n，也就是插入数组一的元素个数，再加上指针搜索插入位置的移动长度，最坏情况等于数组一的长度m
空间复杂度：O（1），常数次空间
func merge(nums1 []int, m int, nums2 []int, n int) { k:=0 for i:=0;i<n;i++{ for nums1[k]<=nums2[i]{ if(k==m) {break} k++ } copy(nums1[k+1:m+1],nums1[k:m]) m++ nums1[k]=nums2[i] } }
链接： https://segmentfault.com/a/1190000041355583
九、中文数字转换为整数
下面是一个用 Go 语言实现的函数，它将中文数字（不超过一亿）转换为整数。代码中考虑了中文数字的各种形式，包括“万”、“千”、“百”等单位，并处理了零的情况。
### 代码说明：
1. **映射表**：
- `chineseNumbers` 用于存储中文数字字符到对应整数的映射。
- `units` 用于存储中文单位字符（如“十”、“百”、“千”、“万”）到其对应数值的映射。
2. **主逻辑**：
- 循环遍历输入字符串中的每个字符。
- 如果字符是中文数字，则将其添加到当前累计值 `current`。
- 如果字符是单位，更新 `current` 的值。如果遇到“万”，则将 `current` 加入到 `result` 中，并重置 `current` 为 0。
- 最后将任何剩余的 `current` 添加到结果 `result` 中。
3. **错误处理**：
- 对于无效字符，返回错误。
### 示例输出：
对于输入 `"六千四百八十五万七千四百零八"`，输出将是：
```
The integer value is: 64857408
```
func chineseToInt(s string) (int, error) { chineseNumbers := map[rune]int{ '零': 0, '一': 1, '二': 2, '三': 3, '四': 4, '五': 5, '六': 6, '七': 7, '八': 8, '九': 9, } units := map[rune]int{ '十': 10, '百': 100, '千': 1000, '万': 10000, } // 清理输入，移除多余的空格并统一为半角 s = strings.TrimSpace(s) result := 0 current := 0 for _, ch := range s { if num, exists := chineseNumbers[ch]; exists { current += num } else if unit, exists := units[ch]; exists { if unit == 10 && current == 0 { current = 1 // "十"前面没有数字时，视为 "一十" } current *= unit if unit == 10000 { result += current current = 0 } } else { return 0, fmt.Errorf("invalid character: %c", ch) } } result += current return result, nil } func main() { input := "六千四百八十五万七千四百零八" result, err := chineseToInt(input) if err != nil { fmt.Println("Error:", err) } else { fmt.Printf("The integer value is: %d\n", result) } }
十、最大连续子数组和
### 代码说明：
- **maxSubArray 函数**：
- 输入一个整数数组 `nums`。
- 使用两个变量 `maxSum` 和 `currentSum` 来跟踪最大和当前的连续子数组和。
- 使用 `start`, `end`, 和 `tempStart` 来记录当前的子数组的起始和结束索引。
- 当 `currentSum` 小于零时，重置 `currentSum` 并更新 `tempStart` 为当前元素的索引。
- 如果找到一个更大的 `currentSum`，则更新 `maxSum` 并记录新的子数组的起始和结束位置。
### 运行结果：
对于输入 `arr := []int{-2, 1, -3, 4, -1, 2, 1, -5, 4}`，输出将是：
```
Maximum subarray: [4 -1 2 1]
Maximum sum: 6
```
该代码能够处理所有情况，包括整个数组为负数。这种情况下，它将返回数组中最大的单个元素。
func maxSubArray(nums []int) ([]int, int) { if len(nums) == 0 { return nil, 0 } maxSum := nums[0] currentSum := nums[0] start := 0 end := 0 tempStart := 0 for i := 1; i < len(nums); i++ { if currentSum < 0 { currentSum = nums[i] tempStart = i // reset the start index } else { currentSum += nums[i] } if currentSum > maxSum { maxSum = currentSum start = tempStart end = i // update end index } } return nums[start : end+1], maxSum } func main() { arr := []int{-2, 1, -3, 4, -1, 2, 1, -5, 4} subArray, sum := maxSubArray(arr) fmt.Printf("Maximum subarray: %v\n", subArray) fmt.Printf("Maximum sum: %d\n", sum) }
十一、零钱凑数
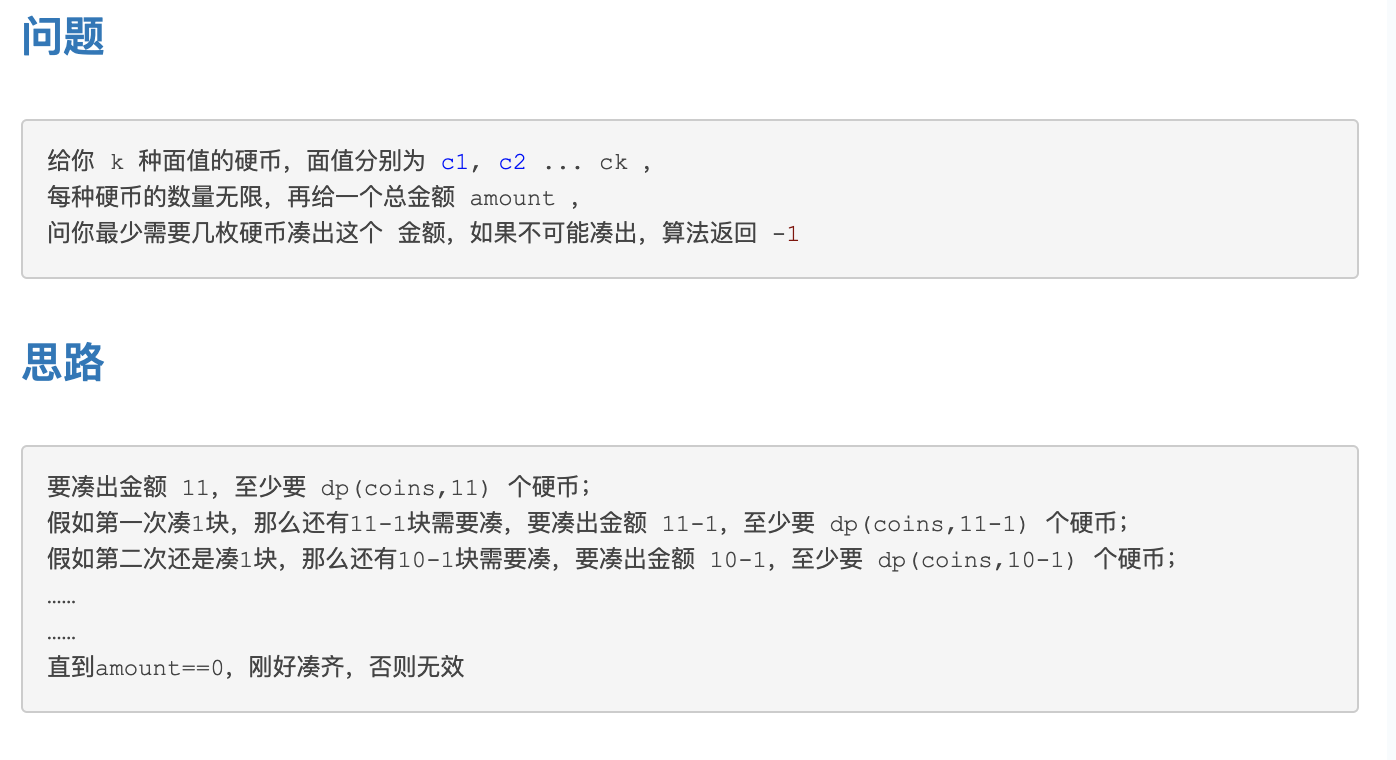
map优化
// coinChange 计算最少需要多少硬币来凑成指定金额 func coinChange(coins []int, amount int) int { // 定义备忘录 count := make([]int, amount+1) for i := range count { count[i] = math.MaxInt32 // 初始化为最大值 } count[0] = 0 // 零金额需要零个硬币 res := help(coins, count, amount) return res } // help 函数进行递归DFS遍历所有可能性 func help(coins []int, count []int, amount int) int { // 如果备忘录中已经保存结果 if count[amount] < math.MaxInt32-1 { // 直接返回 return count[amount] } minRes := math.MaxInt32 for _, coin := range coins { if amount-coin >= 0 { // 递归调用 res := help(coins, count, amount-coin) if res >= 0 && res < minRes { minRes = res + 1 } } } // 更新备忘录 if minRes == math.MaxInt32 { count[amount] = -1 } else { count[amount] = minRes } // 返回结果 return count[amount] } func main() { coins := []int{1, 2, 5} amount := 11 result := coinChange(coins, amount) fmt.Println(result) // 输出最少需要的硬币数 }
复杂度分析
时间复杂度： 时间复杂度为O(mn)，其中m为coins中元素的个数，n为要兑换的总金额。
空间复杂度： 空间复杂度为O(n)，n为要兑换的总金额。
#
链接： https://www.ldtiger.com/pages/289b40/#c-%E4%BB%A3%E7%A0%81
十二、合并两个有序数组，寻找第k大的数
我们先来分析看看： 想到对数的效率，首先想到的就是二分查找，对于这个题目二分查找的意义在哪里呢？
n和m分别表示两个数组的长度
a、如果A[n/2] == B[m/2]，那么很显然，我们的讨论结束了。A[n/2]就已经是中位数，这个和他们各自的长度是奇数或者偶数无关。
b、如果A[n/2] < B[m/2]，那么，我们可以知道这个中位数肯定不在[A[0]---A[n/2])这个区间内，同时也不在[B[m/2]---B[m]]这个区间里面。这个时候，我们不能冲动地把[A[0]---A[n/2])和[B[m/2]---B[m]]全部扔掉。我们只需要把[B[m-n/2]---B[m]]和[A[0]---A[n/2])扔掉就可以了。（如图所示的红色线框），这样我们就把我们的问题成功转换成了如何在A[n/2]->A[n]这个长度为 n/2 的数组和 B[1]-B[m-n/2]这个长度为m-n/2的数组里面找中位数了，问题复杂度即可下降了。
c、只剩下A[n/2] > B[m/2]，和b类似的，我们可以把A[n/2]->A[n]这块以及B[1]->B[n/2]这块扔掉了就行，然后继续递归。
我们也可以写出如下的代码
package main import "fmt" func findKNum(nums1,nums2 []int,k int) int{ len1,len2:=len(nums1),len(nums2) if k>=len1+len2{ return -1 } if len1>len2{ return findKNum(nums2,nums1,k) } if len1==0{ return nums2[k-1] } if k==1{ return min(nums1[0],nums2[0]) } i:=min(len1,k/2) j:=min(len2,k/2) if nums1[i-1]<nums2[j-1]{ return findKNum(nums1[i:],nums2,k-i) }else{ return findKNum(nums1,nums2[j:],k-j) } } func min(a,b int)int{ if a<b{ return a } return b } func main(){ nums1:=[]int{1,2,3,4,5,6} nums2:=[]int{1,2,3,4,5,6,7,8,9,10,11,12} fmt.Println("k:",findKNum(nums1,nums2,19)) }
