最大子数组 && 最大子矩阵

 

 

 

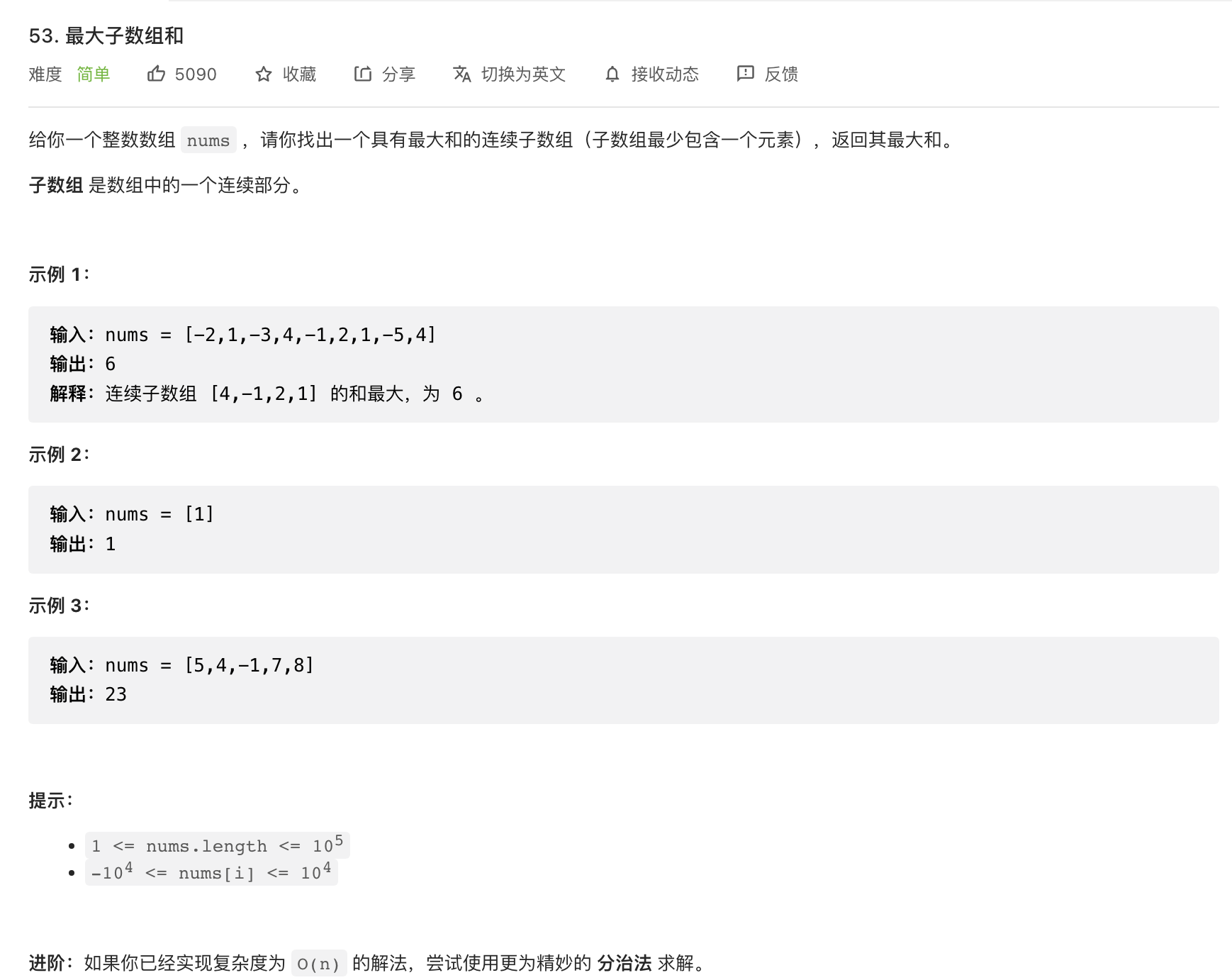
https://leetcode.cn/problems/maximum-subarray/

 

func maxSubArray(nums []int) int {
    maxAns:=-99999999999
    len:=len(nums)
    ans:=0;begin:=0
    le:=0;ri:=len-1
    for i:=0;i<len;i++{
        ans=ans+nums[i]
        if ans>=maxAns{
            maxAns=ans
            le=begin
            ri=i
        }
        if ans<0{
            ans=0
            begin=i+1
        }
    }
    fmt.Println(maxAns,le,ri)
    // tttt:=0

    // for i:=le;i<=ri;i++{
    //     tttt=tttt+nums[i]
    // }

    return maxAns
}

 

 

 

 

 

 

https://leetcode.cn/problems/max-submatrix-lcci/solution/zui-da-zi-ju-zhen-da-liang-tu-pian-zhu-s-cc13/

 

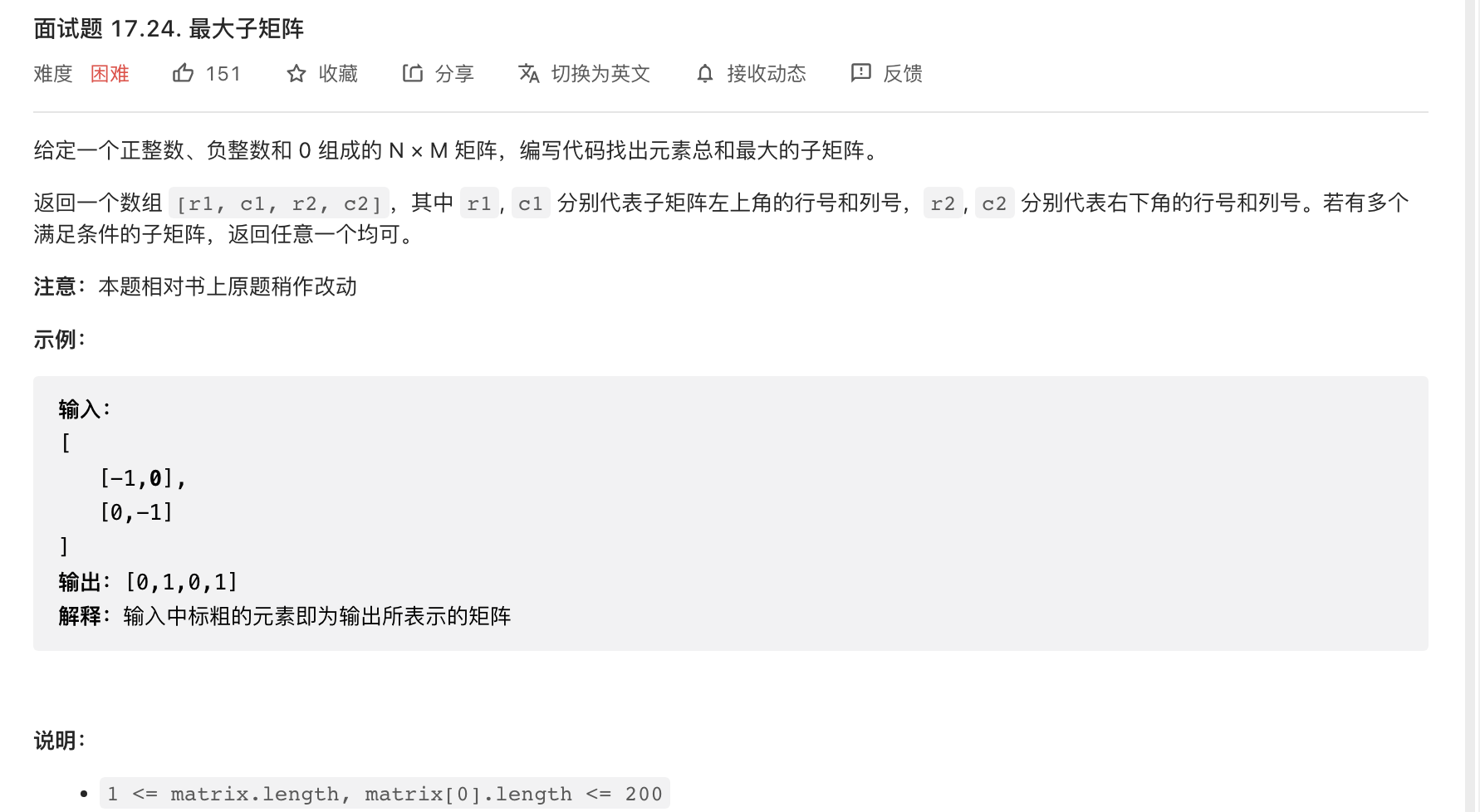
思路：

1、先求以列为维度的前缀和，preSum[i]表示第i列数据，长度为[bedinRow,endRow]的前缀和，endRow是递增的变量

2、在高为endRow-beginRow+1的矩阵中，最大矩阵和就是preSum最大子数组之和

func getMaxMatrix(matrix [][]int) []int{
    row:=len(matrix);col:=len(matrix[0])
    ans:=make([]int,4)//ans[0]和ans[1]分别表示左上角的坐标，ans[2]和ans[3]分表表示右下角的坐标
    maxAns:=matrix[0][0]

    for beginRow:=0;beginRow<row;beginRow++{//先固定矩阵的开始行
        preSum := make([]int,col)          //保存的是按列为数组的前缀和，preSum[i]长度为[beginRow，endRow]的数组中，第i列的前缀和
        for endRow:=beginRow;endRow<row;endRow++{//在固定矩阵结束行

            nowAns:=-999999999;begin:=0
            for i:=0;i<col;i++{//计算当前列数组的最大子数组和
                preSum[i]=preSum[i]+matrix[endRow][i] //其实这里的变量是endRow,计算第i列，从beginRow到endRow的前缀和
                if nowAns>0{
                    nowAns=nowAns+preSum[i]
                }else{
                    nowAns=preSum[i]
                    begin=i
                }

                if maxAns<nowAns{ //维护最大子矩阵的坐标
                    ans[0]=beginRow
                    ans[1]=begin
                    ans[2]=endRow
                    ans[3]=i
                    maxAns=nowAns
                }
            }
        }
    }
    return ans
}