二叉搜索树的插入、删除、查找

二叉查找树有以下性质：

（1）若左子树不空，则左子树上所有节点的值均小于它的根节点的值

（2）若右子树不空，则右子树上所有节点的值均大于它的根节点的值

（3）左、右子树也分别为二叉排序树

（4）没有键值相等的节点

 

插入（递归）

　　插入的数据之后要满足二叉树的性质1和2，所以要先找到插入位置，且插入的位置一定是在叶子节点的下面

　　所以插入分两个步骤：

　　1、确定插入位置是在那个叶子节点下面

　　2、新建一个节点，让叶子节点指向新建的节点

　　

node* insert(node* root,int x)
{
    //插入的位置一定是在叶子节点，这里是先递归找到叶子节点，
    if(root==NULL)
    {
        //然后新建一个节点，让叶子节点指向这个节点
        node *temp=(struct node*)malloc(sizeof(struct node));
        temp->data=x;
        temp->left=NULL;
        temp->right=NULL;
        return temp;
    }
    if(x<root->data)
    {
        root->left=insert(root->left,x);
    }
    else
        root->right=insert(root->right,x);
    return root;//插入的时候是递归，所以最后会返回根节点
}

 

查找（递归）

　　从根节点不断往下找就行

　　

bool search(node * root,int x)
{
    //递归到子节点任然没找到，说明不存在这个节点
    if(root==NULL)
        return false;
    else if(x<root->data)
        return search(root->left,x);
    else if(x>root->data)
        return search(root->right,x);
    else
        return true;
}

 

删除（递归）

　　删除的时候比较复杂，因为删除的节点不一定是在叶子节点上，有可能在其它位置，删除一个节点后还要维持二叉树的完整和树的性质

　　

　　如何维持二叉查找树的完整和性质呢?

　　1、先说如何维持树的完整性：

　　找到被删除节点的位置之后，我们不直接把这个节点删除，而是从被删除节点的子树中找到一个后继节点，用后继节点的值去替换被删除的节点，

　　然后删除后继节点（这里有一个递归，会递归到子节点，最后变成删除叶子节点，删除叶子节点就不会影响树的完整）

 

　　2、如何维持二叉查找树的性质，也就是如何找后继节点（这个性质是：左节点比根节点小，右节点比根节点大）

　　1、如果被删除的这个节点既有子树，又有右子树

　　　　从右子树中找一个最小值，这个最小值就是后继节点

　　　　举个例子解释一下：

　　　　

 

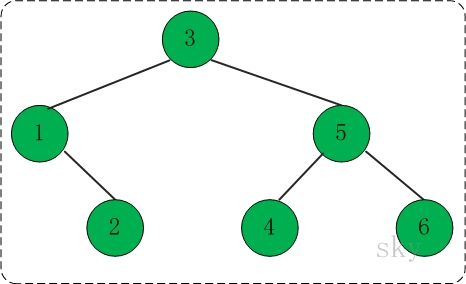
 　　　　如果我要删除值为3的节点，从节点3的右子树中找一个最小值是4，4比右子树中的所有值都大，同时比左子树中所有值都小，所以可以让4去替代3成为根节点

　　代码

//在右子树中查找后继节点（右子树中的最小值）
node* FindMin(node *root)
{
    if(root==NULL)
        return NULL;
    else if(root->left==NULL)
        return root;
    else
        return FindMin(root->left);
}

　　2、如果被删除的这个节点既有只有左子树

　　　　从左节点中找一个最大值成为后继节点，原理同上

　　代码

　　

//在左子树中查找后继节点（左子树中的最大值）
node* FindMax(node *root)
{
    if(root==NULL)
        return NULL;
    else if(root->right==NULL)
        return root;
    else
        return FindMax(root->right);
}

 

　　3、如果被删除的这个节点既有只有右子树

　　从右子树中找一个最小值成为后继节点

 

删除的代码

//删除值为x的节点
node* delet(node* root,int x)
{
    //递归出口是叶子节点
    if(root==NULL)
    {
        return root;
    }
    else
    {
        if(x<root->data)
            root->left=delet(root->left,x);
        else if(x>root->data)
            root->right=delet(root->right,x);
        else
        {
            //左右节点都存在
           if(root->left&&root->right)
           {
                node* temp=FindMin(root->right);
                //把当前节点的值修改成后继节点的值
                root->data=temp->data;
                //在右子树中找后继节点的位置，并删除
                root->right=delet(root->right,root->data);
           }
           else
           {
                //只存在一个子节点
                if(root->left==NULL)
                    root=root->right;
                if(root->right==NULL)
                    root=root->left;
           }
        } 
    }
    return root;//返回根节点
}

 

 

遍历（递归）

　　树的遍历有三种方式：前序、后序、中序

　　

void inOrder(node* root)//以中序序列输出
{
    if(root->left != NULL ) //输出左节点
        inOrder(root->left);
    cout << root->data << " ";//输出根节点
    if(root->right != NULL ) 
        inOrder(root->right);//输出右节点
}
void preOrder(node* root)//以先序序列输出
{
    cout << root->data << " ";//根
    if(root->left!=NULL)
        preOrder(root->left);//左
    if(root->right!=NULL)
        preOrder(root->right);//右
}
void houOrder(node* root)//后序序列输出
{
    if(root->left!=NULL)//左
        houOrder(root->left);
    if(root->right!=NULL)//右
        houOrder(root->right);
    cout << root->data << " ";//根
}

 

 

完整代码

#include<iostream>
#include<stdlib.h>
#include<string.h>
using namespace std;
struct node
{
    int data;
    struct node* left;
    struct node* right;
};
//查找值为x的节点是否在二叉树
bool search(node * root,int x)
{
    //递归到子节点任然没找到，说明不存在这个节点
    if(root==NULL)
        return false;
    else if(x<root->data)
        return search(root->left,x);
    else if(x>root->data)
        return search(root->right,x);
    else
        return true;
}
//向树中插入一个节点
node* insert(node* root,int x)
{
    //插入的位置一定是在叶子节点，这里是先递归找到叶子节点，
    if(root==NULL)
    {
        //然后新建一个节点，让叶子节点指向这个节点
        node *temp=(struct node*)malloc(sizeof(struct node));
        temp->data=x;
        temp->left=NULL;
        temp->right=NULL;
        return temp;
    }
    if(x<root->data)
    {
        root->left=insert(root->left,x);
    }
    else
        root->right=insert(root->right,x);
    return root;//插入的时候是递归，所以最后会返回根节点
}
//在左子树中查找后继节点（左子树中的最大值）
node* FindMax(node *root)
{
    if(root==NULL)
        return NULL;
    else if(root->right==NULL)
        return root;
    else
        return FindMax(root->right);
}

//在右子树中查找后继节点（右子树中的最小值）
node* FindMin(node *root)
{
    if(root==NULL)
        return NULL;
    else if(root->left==NULL)
        return root;
    else
        return FindMin(root->left);
}

//删除值为x的节点
node* delet(node* root,int x)
{
    //递归出口是叶子节点
    if(root==NULL)
    {
        return root;
    }
    else
    {
        if(x<root->data)
            root->left=delet(root->left,x);
        else if(x>root->data)
            root->right=delet(root->right,x);
        else
        {
            //左右节点都存在
           if(root->left&&root->right)
           {
                node* temp=FindMin(root->right);
                //把当前节点的值修改成后继节点的值
                root->data=temp->data;
                //在右子树中找后继节点的位置，并删除
                root->right=delet(root->right,root->data);
           }
           else
           {
                //只存在一个子节点
                if(root->left==NULL)
                    root=root->right;
                if(root->right==NULL)
                    root=root->left;
           }
        } 
    }
    return root;//返回根节点
}
void PrintBSTree(node *root)//前序遍历输出
{
    if(root==NULL)
        return ;
    else
    {
        cout<<root->data<<' ';
        PrintBSTree(root->left);
        PrintBSTree(root->right);
    }
}
void inOrder(node* root)//以中序序列输出
{
    if(root->left != NULL ) //输出左节点
        inOrder(root->left);
    cout << root->data << " ";//输出根节点
    if(root->right != NULL ) 
        inOrder(root->right);//输出右节点
}
void preOrder(node* root)//以先序序列输出
{
    cout << root->data << " ";//根
    if(root->left!=NULL)
        preOrder(root->left);//左
    if(root->right!=NULL)
        preOrder(root->right);//右
}
void houOrder(node* root)//后序序列输出
{
    if(root->left!=NULL)//左
        houOrder(root->left);
    if(root->right!=NULL)//右
        houOrder(root->right);
    cout << root->data << " ";//根
}

int main()
{
    int x,n;
    node* root=new node;
    root=NULL;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>x;
        root=insert(root,x);
    }
    
    preOrder(root);
    cout<<endl;
    delet(root,4);
    preOrder(root);
    cout<<endl;
    
    return 0;
}