hdu 1533 Going Home 最小费用最大流 （模板题）

Going Home

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7405    Accepted Submission(s): 3907

Problem Description

On a grid map there are n little men and n houses. In each unit time, every little man can move one unit step, either horizontally, or vertically, to an adjacent point. For each little man, you need to pay a $1 travel fee for every step he moves, until he enters a house. The task is complicated with the restriction that each house can accommodate only one little man.

Your task is to compute the minimum amount of money you need to pay in order to send these n little men into those n different houses. The input is a map of the scenario, a '.' means an empty space, an 'H' represents a house on that point, and am 'm' indicates there is a little man on that point.

You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.

 

 

Input

There are one or more test cases in the input. Each case starts with a line giving two integers N and M, where N is the number of rows of the map, and M is the number of columns. The rest of the input will be N lines describing the map. You may assume both N and M are between 2 and 100, inclusive. There will be the same number of 'H's and 'm's on the map; and there will be at most 100 houses. Input will terminate with 0 0 for N and M.

 

 

Output

For each test case, output one line with the single integer, which is the minimum amount, in dollars, you need to pay.

 

 

Sample Input

2 2

.m

H.

5 5

HH..m

.....

.....

.....

mm..H

7 8

...H....

...H....

...H....

mmmHmmmm

...H....

...H....

...H....

0 0

 

 

Sample Output

2

10

28

题意：一群人在操场玩耍，突然下起了大雨，大家匆忙找房子躲雨，每走一步会消耗一卡路里，问所有人躲到房子里面最少会花费多少卡路里。

m代表人,H代表房子，一间房子只能容纳一个人，如果房子里面有人，其他人可以从房子经过，但躲不了雨。

 

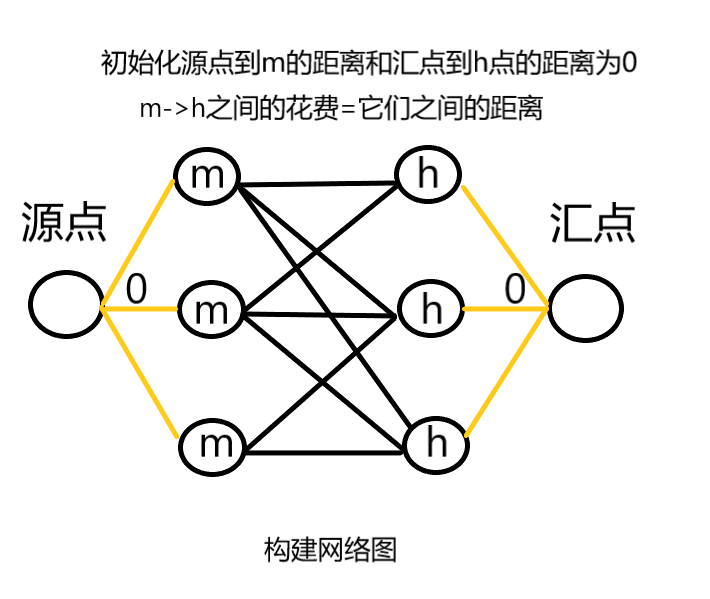
题解：输入中的每个人和房子可以组成一条条边，我们用一个源点和汇点把所有边统一起来，组成一个网络图，在这个网络图中求需要的最小花费

 

 

#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
#include<queue>
#define ll long long
#define mx 0x3f3f3f3f
using namespace std;
int cap[500][500],cost[500][500],flow[500][500];//cap是容量，cost是花费，flow是流量
int pre[500],dis[500],vis[500],cnt[500];//pre是记录增广路的前驱节点，dis[i]是记录源点到节点i的最小距离
//vis[i]标记点是否在队列中，cnt[i]记录点i进入队列的次数
char str[500][500];
struct node
{
    int x;
    int y;
}s[500],e[500];

int n,m;
int st,endd,nn,mm;//st是源点，endd是汇点
int mn_cost,mx_flow;
int spfa()
{
    for(int i=0;i<n;i++)
        dis[i]=mx;
    memset(vis,0,sizeof(vis));
    memset(cnt,0,sizeof(cnt));
    
    queue<int>p;
    p.push(st);//st是起点
    vis[st]=1;
    cnt[st]=1;
    dis[st]=0;
    while(!p.empty())
    {
        int now=p.front();
        p.pop();
        vis[now]=0;
        for(int i=0;i<n;i++)
        {
            if(cap[now][i]>flow[now][i]&&dis[i]>dis[now]+cost[now][i])//这里将费用看成是长度，求源点到汇点的最小距离
            {
                dis[i]=dis[now]+cost[now][i];
                pre[i]=now;
                if(vis[i]==0)
                {
                    p.push(i);
                    vis[i]=1;
                    cnt[i]++;
                    if(cnt[i]>n)
                        return 0;
                }
            }
        }
    }
    if(dis[endd]>=mx)
        return 0;
    return 1;
}
void bfs(int n)//顶点数
{
    memset(flow,0,sizeof(flow));
    mx_flow=0;
    mn_cost=0;
    while(spfa())
    {
        int f=mx;
        for(int i=endd;i!=st;i=pre[i])
            f=min(f,cap[pre[i]][i]-flow[pre[i]][i]);

        for(int i=endd;i!=st;i=pre[i])//更新流量
        {
            flow[pre[i]][i]+=f;
            flow[i][pre[i]]-=f;
        }
        mn_cost+=dis[endd]*f;
        mx_flow+=f;

    }
}
int main()
{
    while(~scanf("%d%d",&nn,&mm)&&nn&&mm)
    {
        //这道题需要自己将输入转化，建立一个有向图
        int cnt1=0,cnt2=0;
        for(int i=0;i<nn;i++)
        {
            scanf("%s",str[i]);
            for(int j=0;j<mm;j++)
            {
                if(str[i][j]=='m')//起点
                {
                    cnt1++;
                    s[cnt1].x=i;
                    s[cnt1].y=j;
                }
                if(str[i][j]=='H')//终点
                {
                    cnt2++;
                    e[cnt2].x=i;
                    e[cnt2].y=j;
                }
            }
        }
        n=cnt1+cnt2+2;//加上源点和汇点，共有n个点，[0,n-1]
        st=0;//源点
        endd=cnt1+cnt2+1;//汇点
        memset(cap,0,sizeof(cap));
        memset(cost,0,sizeof(cost));
        for(int i=1;i<=cnt1;i++)//初始化源点到任意起点的花费为0，容量为1；
        {
            cap[0][i]=1;
            cost[0][i]=0;
            cost[i][0]=0;
        }
        for(int i=1;i<=cnt2;i++)//初始化汇点到所有终点的花费为0，容量为1；
        {
            cap[i+cnt1][endd]=1;
            cost[i+cnt1][endd]=0;
            cost[endd][i+cnt1]=0;
        }
        for(int i=1;i<=cnt1;i++)//初始化起点到终点的花费和容量
        {
            for(int j=1;j<=cnt2;j++)
            {
                cap[i][cnt1+j]=1;
                cost[i][cnt1+j]=abs(s[i].x-e[j].x)+abs(s[i].y-e[j].y);
                cost[cnt1+j][i]=-cost[i][cnt1+j];
            }
        }
        bfs(n);
        printf("%d\n",mn_cost);
    }
    return 0;
}