最小生成树（Kruskal+Prim）--模板

最小生成树-----在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

 

应用场景

1、假设以下情景，有一块木板，板上钉上了一些钉子，这些钉子可以由一些细绳连接起来。假设每个钉子可以通过一根或者多根细绳连接起来，那么一定存在这样的情况，

即用最少的细绳把所有钉子连接起来。

2、更为实际的情景是这样的情况，在某地分布着N个村庄，现在需要在N个村庄之间修路，每个村庄之前的距离不同，问怎么修最短的路，将各个村庄连接起来。

以上这些问题都可以归纳为最小生成树问题，用正式的表述方法描述为：给定一个无方向的带权图G=(V, E)，最小生成树为集合T, T是以最小代价连接V中所有顶点所用边E的最小集合。 集合T中的边能够形成一颗树，这是因为每个节点（除了根节点）都能向上找到它的一个父节点。

 

一、kruskal（克鲁斯卡尔）

先对所有边进行排序，以权值最小的边所在的点为根节点开始处理，用一个for循遍历所有排序后的边，若这条边的两个点的根节点不同，累加上权值，再把这两个点合并，一直处理到最后即可
需要用到并查集知识（并查集的加边操作记得用路径压缩，避免超时），和结构体的排序

模板：

int p[100005],r[100005];
int n,ans;
struct node
{
  int x;//x,y是坐标，v是权值
  int y;
  int v;
}a[100005];
bool cmp(node b,node c)
{
  return b.v<c.v;
}
int find(int x)//查找元素x的老板是谁
{
    if (x == p[x])
        return x;
    else
        return p[x] = find(p[x]);
}

void join(int x, int y)//路径压缩合并两个集合
{
    int xRoot = find(x);
    int yRoot = find(y);

    if (xRoot == yRoot) //老板相同，不合并
        return;
    //cnt=cnt-1;
    if (r[xRoot] < r[yRoot]) //r[i]是元素i所在树的高度，矮树的根节点认高树的根节点做老板
        p[xRoot] = yRoot;
    else if (r[xRoot] > r[yRoot])
        p[yRoot] = xRoot;
    else
    {
        p[yRoot] = xRoot;//树高相同，做老板的树高度要加一
        r[xRoot]++;
    }
}
void kruskal()
{
  for(int i=1;i<=n;i++)//初始化根节点
    p[i]=i;
  sort(a+1,a+n*(n-1)/2+1,cmp);
  for(int i=1;i<=n*(n-1)/2;i++)
  {
    if(find(a[i].x)!=find(a[i].y))
    {
      join(a[i].x,a[i].y);
      ans=ans+a[i].v;
    }
  }
}

 

 

二、Prime(普里姆)

由顶点开始（可以随便找一个为顶点）形成一个点集，每次从剩余点中找一个与这个点集最近的点（权值最小的点）并加入点集，直到结束

以下流程图转载自https://blog.csdn.net/lqcsp/article/details/14118871，谢谢博主^-^

   知道了普利姆算法的核心步骤，下面我就用图示法来演示一下工作流程，如图：

 

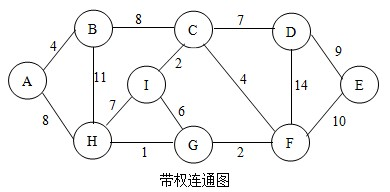
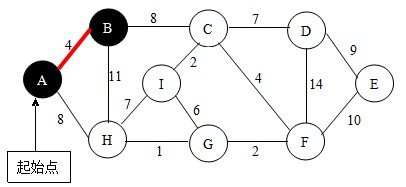
首先，确定起始顶点。我以顶点A作为起始点。根据查找法则，与点A相邻的点有点B和点H，比较AB与AH，我们选择点B，如下图。并将点B加入到U中。

 

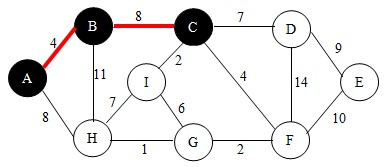
继续下一步，此时集合U中有{A,B}两个点，再分别以这两点为起始点，根据查找法则，找到边BC（当有多条边权值相等时，可选任意一条），如下图。并将点C加入到U中。

 

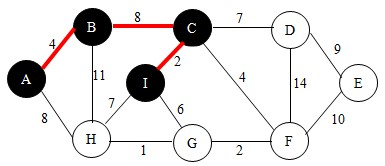
继续，此时集合U中有{A,B,C}三个点，根据查找法则，我们找到了符合要求的边CI，如下图。并将点I加入到U中。

 

继续，此时集合U中有{A,B,C,I}四个点，根绝查找法则，找到符合要求的边CF，如下图。并将点F加入到集合U中。

 

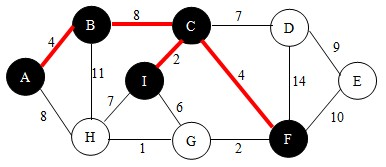
继续，依照查找法则我们找到边FG,如下图。并将点G加入到U中。

 

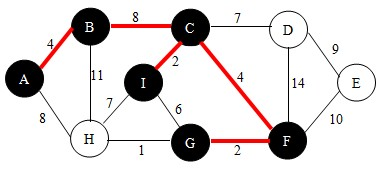
继续，依照查找法则我们找到边GH,如下图。并将点H加入到U中。

 

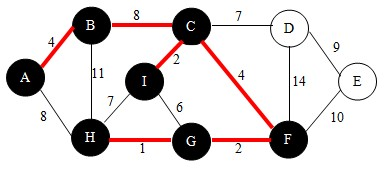
继续，依照查找法则我们找到边CD,如下图。并将点D加入到U中。

 

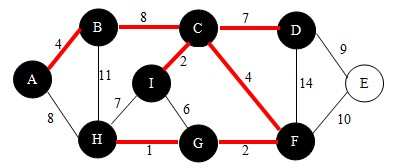
继续，依照查找法则我们找到边DE,如下图。并将点E加入到U中。

 

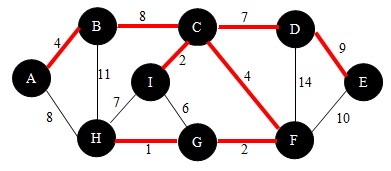
此时，满足U = V，即找到了这颗最小生成树。

模板：

void prim()
{
  ans=0;
  memset(vis,0,sizeof(vis));
  for(int i=2;i<=n;i++)//初始化
    dis[i]=a[1][i];
  dis[1]=0;
  vis[1]=1;

  for(int i=1;i<n;i++)//最后一个点不需要处理，直接加入即可，所以不要（也不能）取等
  {
    int k=0,mn=9999999;
    for(int j=1;j<=n;j++)//找出还没有被标记的点中离起点权值最小的点
    {
      if(!vis[j]&&dis[j]<mn)
      {
        mn=dis[j];
        k=j;
      }
    }
    vis[k]=1;
    ans=ans+mn;
    for(int j=1;j<=n;j++)//更新最小值，k和起点都在处理过的集合里面，更新到起点的最小值
    {
      if(!vis[j]&&dis[j]>a[k][j])
        dis[j]=a[k][j];
    }
  }

}

 

 模板题：hdu1233 还是畅通工程 https://www.cnblogs.com/-citywall123/p/10999949.html