哈希(hash)理解
转载自https://www.cnblogs.com/mingaixin/p/4318837.html
一、什么是哈希?(一种更复杂的映射)
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入,通过散列算法(哈希函数),变换成固定长度的输出,该输出就是散列值(哈希值)。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出(冲突),所以不可能从散列值来唯一的确定输入值。
映射是一种对应关系,而且集合A的某个元素只能对应集合B中的一个元素。但反过来,集合B中的一个元素可能对应多个集合A中的元素。如果B中的元素只能对应A中的一个元素,这样的映射被称为一一映射。这样的对应关系在现实生活中很常见,比如:
A -> B
人 -> 身份证号
日期 -> 星座
这里的映射都是直接的映射,没有经过函数处理,而哈希就是经过哈希函数处理后的映射
先说明几个概念:
- 键值(函数自变量)、哈希值(因变量):
上面两个映射中,人 -> 身份证号是一一映射的关系。在哈希表中,上述对应过程称为hashing。A中元素a对应B中元素b,a被称为键值(key),b被称为a的hash值(hash value)。
2.哈希表(存储映射关系)、哈希函数(映射法则f(x)):
哈希表是从一个集合A到另一个集合B的映射。哈希表的核心是一个哈希函数(hash function),这个函数规定了集合A中的元素如何对应到集合B中的元素
假设集合A中的元素的元素都是三位以上的整数,哈希函数f(x)的法则为取这个数的个位数作为哈希值,即f(x)=x%10;那么在哈希表中对应的关系就是a[x]=x*%10
3.冲突(碰撞):
两个不同的键值,根据同一哈希函数计算出的哈希值相同的现象叫做冲突(碰撞)。
例如:a[122]=2, a[123]=3,a[124]=4, a[222]=2和a[122]=2的哈希值相同,产生冲突
二、常见的哈希函数
1.直接定址法:直接以关键字k或者k加上某个常数(k+c)作为哈希地址(哈希值)。
f(k)=k*a+b,其中a,b为合理的常数;
2.数字分析法:提取关键字中取值比较均匀的数字作为哈希地址。
例如有某些人的生日数据如下:
年. 月. 日
75.10.03
85.11.23
86.03.02
86.07.12
85.04.21
96.02.15
经分析,第一位,第二位,第三位重复的可能性大,取这三位造成冲突的机会增加,所以尽量不取前三位,取后三位比较好
3.除留余数法:如果知道Hash表的最大长度为m,可以取不大于m的最大质数p,然后对关键字进行取余运算,将所得余数作为哈希表地址。
f(k)=k%p,在这里p的选取非常关键,p选择的好的话,能够最大程度地减少冲突,p一般取不大于m的最大质数。
4.分段叠加法:按照哈希表地址位数将关键字分成位数相等的几部分,其中最后一部分可以比较短。然后将这几部分相加,舍弃最高进位后的结果就是该关键字的哈希地址。
假设知道图书的ISBN号为8903-241-23,可以将address(key)=89+03+24+12+3作为Hash地址。
5.平方取中法:如果关键字各个部分分布都不均匀的话,可以先求出它的平方值,然后按照需求取中间的几位作为哈希地址。
假如有以下关键字序列{421,423,436},平方之后的结果为{177241,178929,190096},那么可以分别取{72,89,00}作为{421,423,436}的Hash地址
6.伪随机数法:采用一个伪随机数当作哈希函数。
f(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。
三、解决碰撞的方法
通过构造性能良好的哈希函数,可以减少冲突,但一般不可能完全避免冲突,因此解决冲突是哈希法的另一个关键问题。创建哈希表和查找哈希表都会遇到冲突,两种情况下解决冲突的方法应该一致。下面以创建哈希表为例,说明解决冲突的方法。常用的解决冲突方法有以下四种:
- 开放定址法:
开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。
这种方法也称再散列法,其基本思想是:当关键字key的哈希地址p=f(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍然冲突,再以p为基础,产生另一个哈希地址p2,…,直到找出一个不冲突的哈希地址pi ,将相应元素存入其中。这种方法有一个通用的再散列函数形式:f i=(f(key)+di)%m i=1,2,…,n,其中f(key)为哈希函数,m 为表长,di称为增量序列。增量序列的取值方式不同,相应的再散列方式也不同。主要有以下三种:
1.线性探测再散列
di=1,2,3,…,m-1
这种方法的特点是:冲突发生时,顺序查看表中下一单元,直到找出一个空单元或查遍全表。
2.二次探测再散列
di=12,-12,22,-22,…,k2,-k2 ( k<=m/2)
这种方法的特点是:冲突发生时,在表的左右进行跳跃式探测,比较灵活。
3.伪随机探测再散列处理
di=伪随机数序列。
具体实现时,应建立一个伪随机数发生器,(如i=(i+p) % m),并给定一个随机数做起点。
下面举例说明上述三种处理方法
假设已知哈希表长度m=11,哈希函数为:f(key)= key % 11,则f(47)=3,f(26)=4,f(60)=5,假设下一个关键字为69,则f(69)=3,与47冲突。
如果用线性探测再散列处理冲突:
下一个哈希地址为f1=(3 + 1)% 11 = 4,仍然冲突,再找下一个哈希地址为f2=(3 + 2)% 11 = 5,还是冲突,继续找下一个哈希地址为f3=(3 + 3)% 11 = 6,此时不再冲突,将69填入5号单元。
如果用二次探测再散列处理冲突:
下一个哈希地址为f1=(3 + 12)% 11 = 4,仍然冲突,再找下一个哈希地址为f2=(3 - 12)% 11 = 2,此时不再冲突,将69填入2号单元。
如果用伪随机探测再散列处理冲突:
假设伪随机数序列为:2,5,9,……..,则下一个哈希地址为f1=(3 + 2)% 11 = 5,仍然冲突,再找下一个哈希地址为f2=(3 + 5)% 11 = 8,此时不再冲突,将69填入8号单元。
从上述例子可以看出,线性探测再散列容易产生“二次聚集”,即在处理同义词的冲突时又导致非同义词的冲突。例如,当表中i, i+1 ,i+2三个单元已满时,下一个哈希地址为i, 或i+1 ,或i+2,或i+3的元素,都将填入i+3这同一个单元,而这四个元素并非同义词。线性探测再散列的优点是:只要哈希表不满,就一定能找到一个不冲突的哈希地址,而二次探测再散列和伪随机探测再散列则不一定。
- 链地址法
- 将哈希表的每个单元作为链表的头结点,所有哈希地址为i的元素构成一个同义词链表。即发生冲突时就把该关键字链在以该单元为头结点的链表的尾部。
这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表,并将单链表的头指针存在哈希表的第i个单元中,因而查找、插入和删除主要在同义词链中进行。若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。链地址法适用于经常进行插入和删除的情况。
- 再哈希法
- 当哈希地址发生冲突用其他的函数计算另一个哈希函数地址,直到冲突不再产生为止。
再散列法其实很简单,就是再使用哈希函数去散列一个输入的时候,输出是同一个位置就再次散列,直至不发生冲突位置
缺点:每次冲突都要重新散列,计算时间增加。
- 建立公共溢出区
- 将哈希表分为基本表和溢出表两部分,发生冲突的元素都放入溢出表中。
这种方法的基本思想是:将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表.(注意:在这个方法里面是把元素分开两个表来存储)
四、简单应用
一、字符串哈希
介绍:关于字符串hash,一句话概括,就是把字符串有效的转化为一个整数,下面介绍一种转化方法:
进制哈希:
首先让我们先回想一下二进制数。
对于任意一个二进制数,我们将它化为10进制的数的方法如下(以二进制数1101101为例):
进制hash用的也是一样的原理
假设两个较大的素数p和mod,把字符串内的每一个字母按前缀和的方式处理,每一次都乘以素数p,再加上当前字符str[i](转化成整数),最后把求得的和对mod取模的值,就是转化后这个字符串对应的哈希值。
假设sum[0]=str[0]
sum[i]=( sum[i-1]*p+str[i] )%mod (i>=1);
for example:
取p=13, mod=101,求字符串str=“abc"对应的整数
sum[0]=str[0]-'a'+1; 表示a映射1。
sum[1]=(sum[0]*13+(int)b)%101=15;表示ab映射15。
sum[2]=(sum[1]*13+(int)c)%101=97; 表示abc映射97。
这样,我们就可以记录下每一个字符串所对应的整数,若下一次出现一个字符串,查询整数是否出现过,就可以完成验证。
但是也有可能出现两个字符串对应一个整数。
调整方法(减少冲突):
调整p和mod,取p和mod都为较大的素数。 p取6~8位素数,一般可取131或13331;mod一般取1e9+7或者1e9+9;
为什么要要用unsigned long long?
如果字符串很多呢?那样不是会溢出了吗?
因此我们把hash值储存在unsigned long long里面, 那样溢出时,会自动取余2的64次方,but这样可能会使2个不同串的哈希值相同,但这样的概率极低(不排除你的运气不好)。
注意:unsigned long long 数据精度很高,对格式的要求也更高,因此在做取模运算时,要注意使用一致的数据类型
简单应用题
 View Code/* 给定N个单词(每个单词长度不超过100,单词字符串内仅包含小写字母)。 请求出N个单词中共有多少个不同的单词。 输入 第1行包含1个正整数N。 接下来N行每行包含一个字符串。 输出 一个整数,代表不同单词的个数 样例输入 5 lalala hahaha haha lalala haha 样例输出 3 提示* N <= 10000000 不同单词个数不超过100000 */ #include<iostream> #include<algorithm> #include<string.h> #define ull unsigned long long using namespace std; ull num[1000005]; ull n,p=1331,mod=1e9+7; ull hs(string str) { ull temp=str[0]; for(int i=1;i<str.length();i++) temp=(temp*p+str[i])%mod; return temp; } int main() { string str; cin>>n; for(int i=0;i<n;i++) { cin>>str; num[i]=hs(str); } sort(num,num+n); int cnt=1; for(int i=1;i<n;i++) { if(num[i-1]!=num[i]) cnt++; } cout<<cnt<<endl; return 0; }
View Code/* 给定N个单词(每个单词长度不超过100,单词字符串内仅包含小写字母)。 请求出N个单词中共有多少个不同的单词。 输入 第1行包含1个正整数N。 接下来N行每行包含一个字符串。 输出 一个整数,代表不同单词的个数 样例输入 5 lalala hahaha haha lalala haha 样例输出 3 提示* N <= 10000000 不同单词个数不超过100000 */ #include<iostream> #include<algorithm> #include<string.h> #define ull unsigned long long using namespace std; ull num[1000005]; ull n,p=1331,mod=1e9+7; ull hs(string str) { ull temp=str[0]; for(int i=1;i<str.length();i++) temp=(temp*p+str[i])%mod; return temp; } int main() { string str; cin>>n; for(int i=0;i<n;i++) { cin>>str; num[i]=hs(str); } sort(num,num+n); int cnt=1; for(int i=1;i<n;i++) { if(num[i-1]!=num[i]) cnt++; } cout<<cnt<<endl; return 0; }
那么,对于一个字符串,怎么提取它[l,r]中的哈希值呢?
我们已经知道这个字符串每一个位置的哈希值,类似与前缀和,即sum[r] - sum[l],但是对于 r 位置的哈希值sum[r],包含它的前一部分([0,l-1]部分),这一部分多乘了(r-l+1)个p
sum[r]=sum[l,r]+sum[l-1]*p(r-l+1)
因此区间[l,r]的哈希值可以表示为
sum[l,r]=sum[r]-sum[l-1]*p(r-l+1)
模板题:poj4300 https://www.cnblogs.com/-citywall123/p/10841081.html




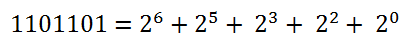



 浙公网安备 33010602011771号
浙公网安备 33010602011771号