并查集---模板

主要操作

初始化

把每个点所在集合初始化为其自身。

通常来说，这个步骤在每次使用该数据结构时只需要执行一次，无论何种实现方式，时间复杂度均为O(N)。

查找

查找元素所在的集合，即根节点。

合并

将两个元素所在的根节点相同，集合合并为一个集合，根节点不同就新建一个集合。

通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的“查找”操作实现。

 

不理解？戳这里https://www.cnblogs.com/xzxl/p/7226557.html

 

注意：要看题意编号是从0开始还是从1开始，模板是从1开始

 

模板一：不进行路径压缩，当前元素的根节点就是它的上一级

 

int p[1000005], r[1000005];
int n,t=0;
void init()//初始化集合，每个元素的老板都是自己
{
    for (int i = 1; i <= n; i++)
    {
        p[i] = i;
    }
}

int find(int x)                        //查找x的掌门
{
    int r=x;                           //委托 r 去找掌门
    while(p[r] != r)                 //如果r的上级不是r自己（也就是说找到的大侠他不是掌门 = =）
        r = p[r] ;                   // r 接着找他的上级，直到找到掌门为止。
    return  r ;                        //掌门驾到~~~
}


void join(int x,int y)                     //我想让虚竹和周芷若做朋友
{
    int xRoot=find(x), yRoot=find(y);             //虚竹的老大是玄慈，芷若MM的老大是灭绝
    if(xRoot != yRoot)                             //玄慈和灭绝显然不是同一个人
        p[xRoot]=yRoot;                       //方丈只好委委屈屈地当了师太的手下啦
}

void num()//求不同子集个数
{
    for(int i=1;i<=n;i++)//有多少个p[i]==i,就有多少个子集
    {
        if(p[i]==i)
            t++;
    }
}
bool sameRoot(int x, int y)//查询两个元素的老板是否相同
{
    return find(x) == find(y);
}

 

 模板二：进行路径压缩，当前元素的上级直接就是根节点

 

 

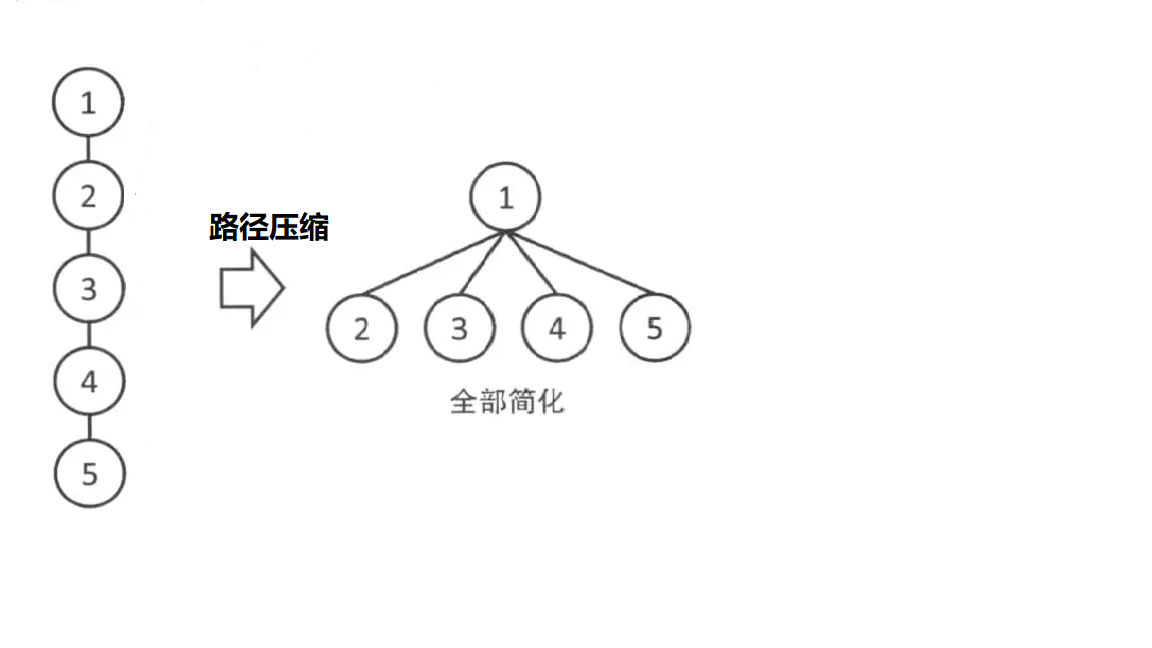
int p[1000005], r[1000005];
int n,t=0,cnt;
void init()//初始化集合，每个元素的老板都是自己
{
    for (int i = 1; i <= n; i++)
    {
        p[i] = i;
    }
}

int find(int x)//查找元素x的老板是谁
{
    if (x == p[x])
        return x;
    else
        return p[x] = find(p[x]);
}

void join(int x, int y)//合并两个集合
{
    int xRoot = find(x);
    int yRoot = find(y);

    if (xRoot == yRoot) //老板相同，不合并
        return;
    //cnt=cnt-1;
    if (r[xRoot] < r[yRoot]) //r[i]是元素i所在树的高度，矮树的根节点认高树的根节点做老板
        p[xRoot] = yRoot;
    else if (r[xRoot] > r[yRoot])
        p[yRoot] = xRoot;
    else
    {
        p[yRoot] = xRoot;//树高相同，做老板的树高度要加一
        r[xRoot]++;
    }
}
void num()//求不同子集个数
{
    for(int i=1;i<=n;i++)//有多少个p[i]==i,就有多少个子集
    {
        if(p[i]==i)
            t++;
    }
}
bool sameRoot(int x, int y)//查询两个元素的老板是否相同
{
    return find(x) == find(y);
}
//这里也可以用cnt求不同子集个数，初始化cnt=n,每加入一条边，cnt=cnt-1;

 

 模板题：https://www.cnblogs.com/-citywall123/p/10717232.html