剪邮票--蓝桥杯--dfs--思路超清晰

剪邮票

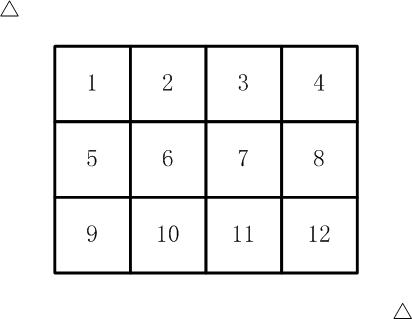
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
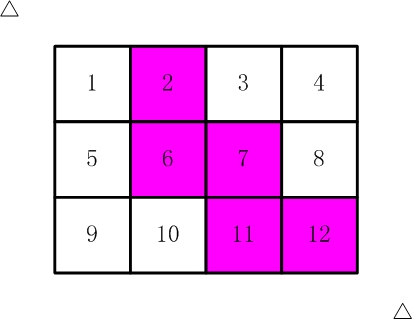
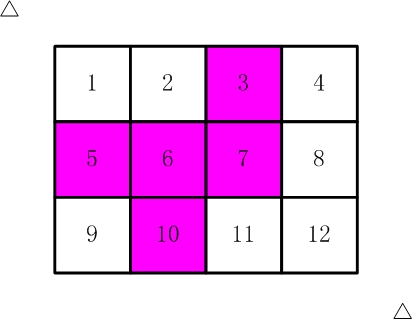
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

题解：用for循环把1~12每一个点作为搜索起点去dfs次，已经作为搜索起点的点不能再被dfs过程中枚举

所得的最后结果再加2；

为什么要加2？
因为我这里搜索的是由起点不断外延伸的，所以cnt只包含了线性连通的情况
这里还有两种放射状连通的情况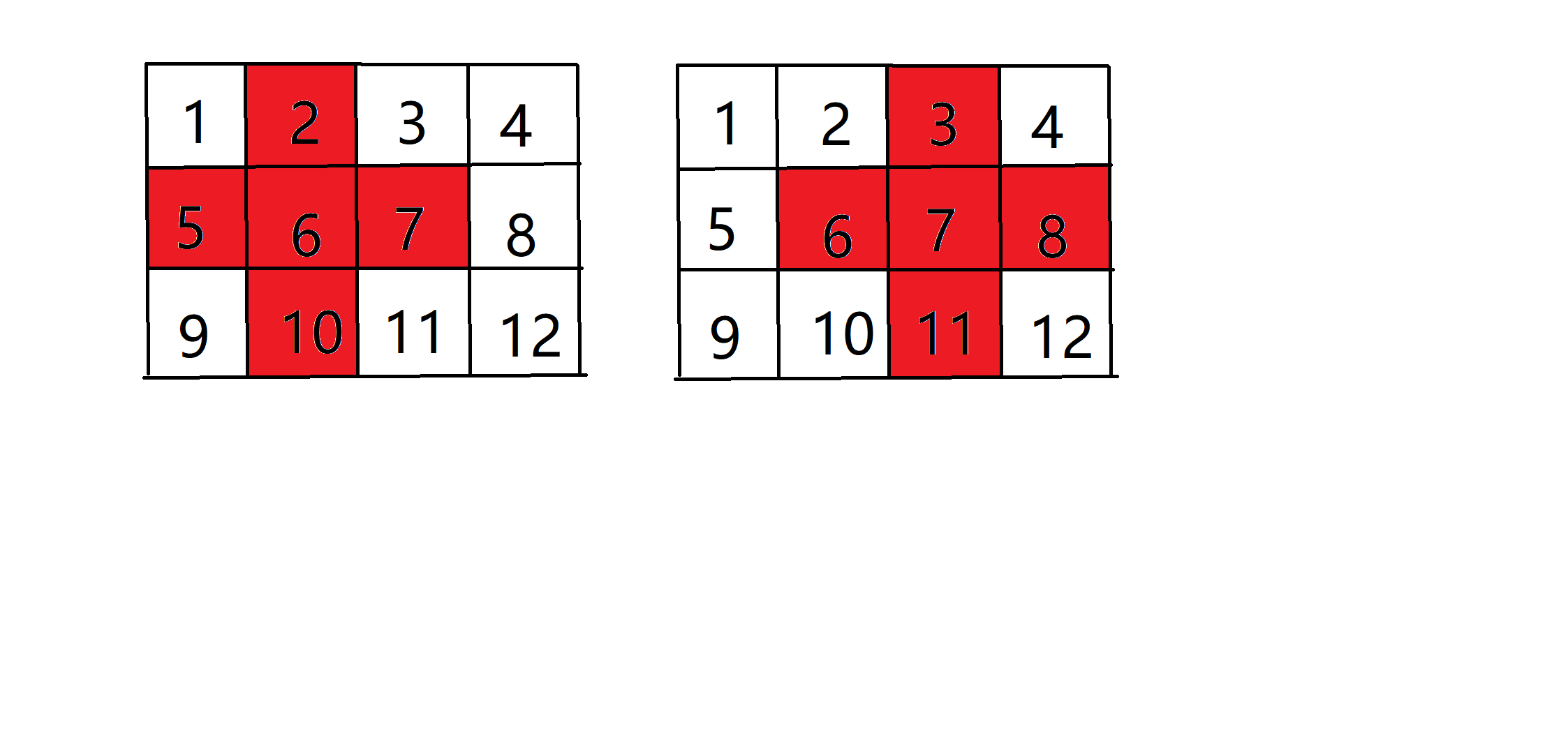

 

 答案：116

#include<iostream>
#include<string.h>
using namespace std;
int a[3][4],star[12],vis[3][4],dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
int cnt=0;
int check(int x,int y)
{
    if(x>=0&&x<3&&y>=0&&y<4)
        return 1;
    else
        return 0;
}
void dfs(int x,int y,int dep)
{
    if(dep==5)
    {
        cnt++;
        return;
    }
    else
    {
        for(int i=0;i<4;i++)
        {
            int tx,ty;
            tx=x+dir[i][1];
            ty=y+dir[i][0];
            if(check(tx,ty)&&!vis[tx][ty]&&!star[a[tx][ty]])//在棋盘内/可以剪/这个点没有作为搜索起点使用过
            {
                vis[tx][ty]=1;
                dfs(tx,ty,dep+1);
                vis[tx][ty]=0;
            }

        }
    }

}
int main()
{
    int n=0;
    for(int i=0;i<3;i++)
    {
        for(int j=0;j<4;j++)
            a[i][j]=n++;
    }
    for(int i=0;i<3;i++)
    {
        for(int j=0;j<4;j++)
        {
            dfs(i,j,0);
            star[a[i][j]]=1;//标记搜索起点，避免重复
        }
    }
    cout<<cnt+2<<endl;//为什么要加2？
                      //因为我这里搜索的是由起点不断外延伸的，所以cnt只包含了线性连通的情况
                      //这里还有两种放射状连通的情况
}