求近似值（快速幂）

A: 求近似值

时间限制: 1 s      内存限制: 128 MB     

 

题目描述

求⌊(5–√+6–√)2n⌋

%9932017。

例如：n=1，(5–√+6–√)2

=21.9544....，⌊(5–√+6–√)2⌋

%9932017=21。

输入

第一行输入T，表示n的个数。（1<=T<=200000）

下面T行每行一个数，表示n。（0<=n<=10^18）

输出

按照题意输出答案。

样例输入

3
0
1
2

样例输出

1
21
481

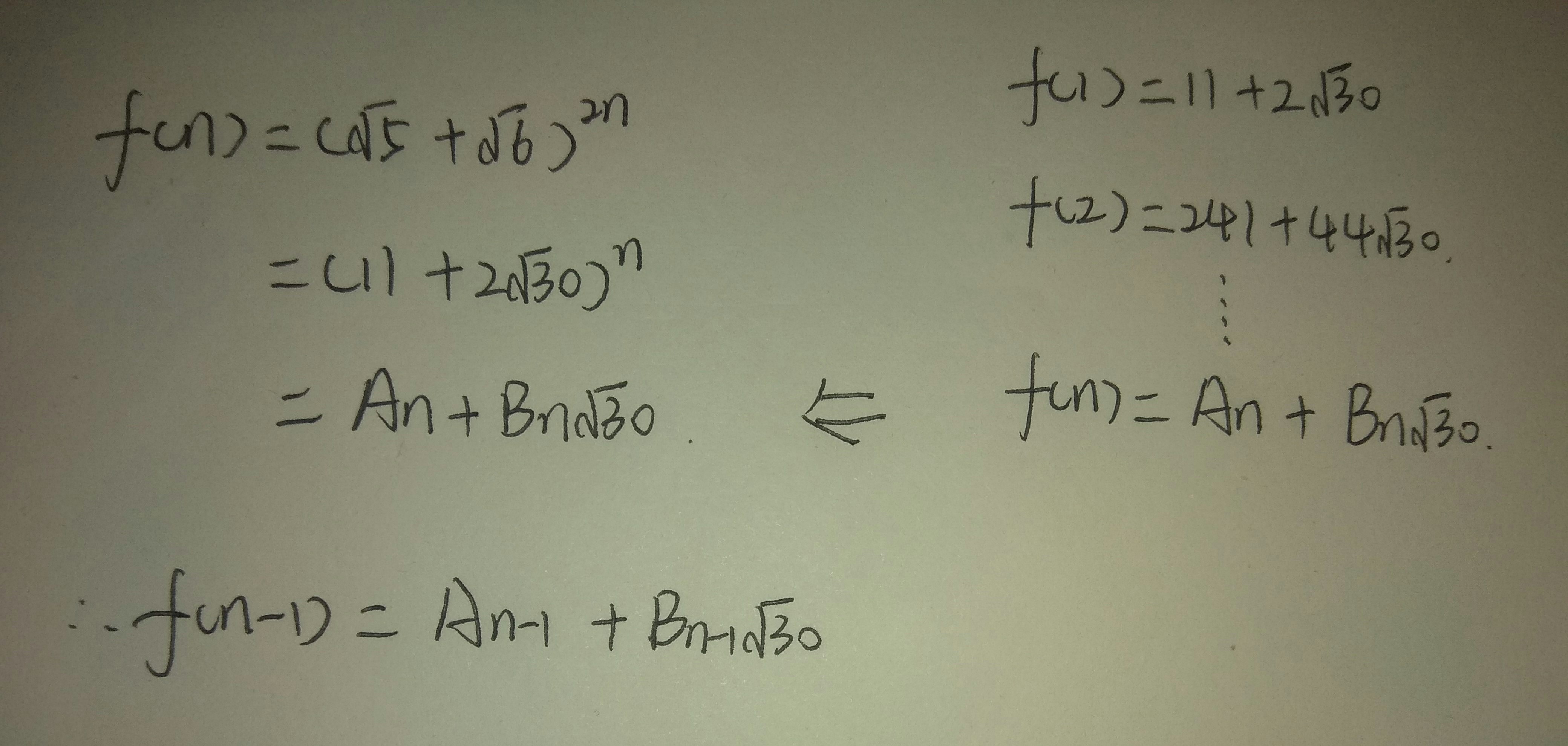
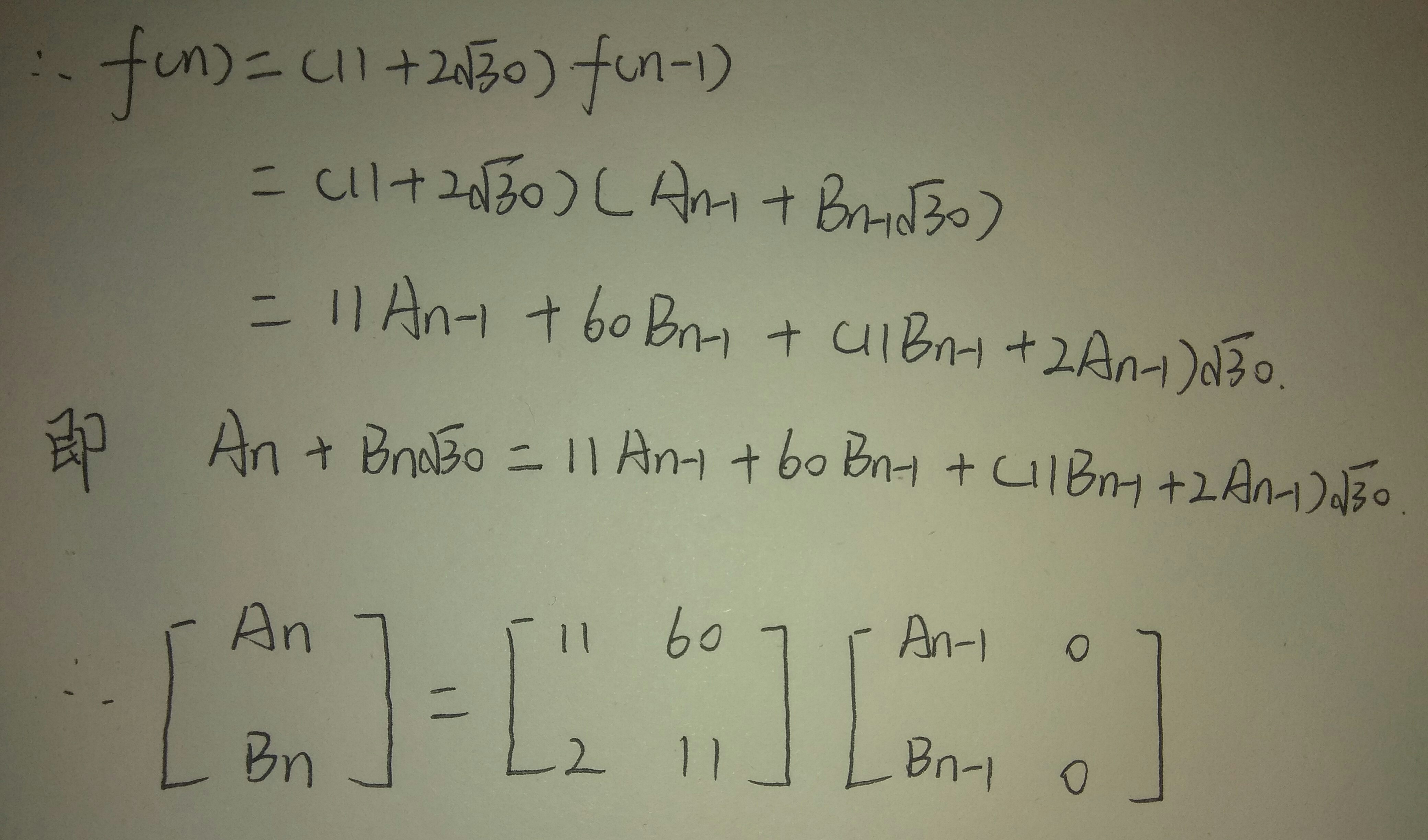
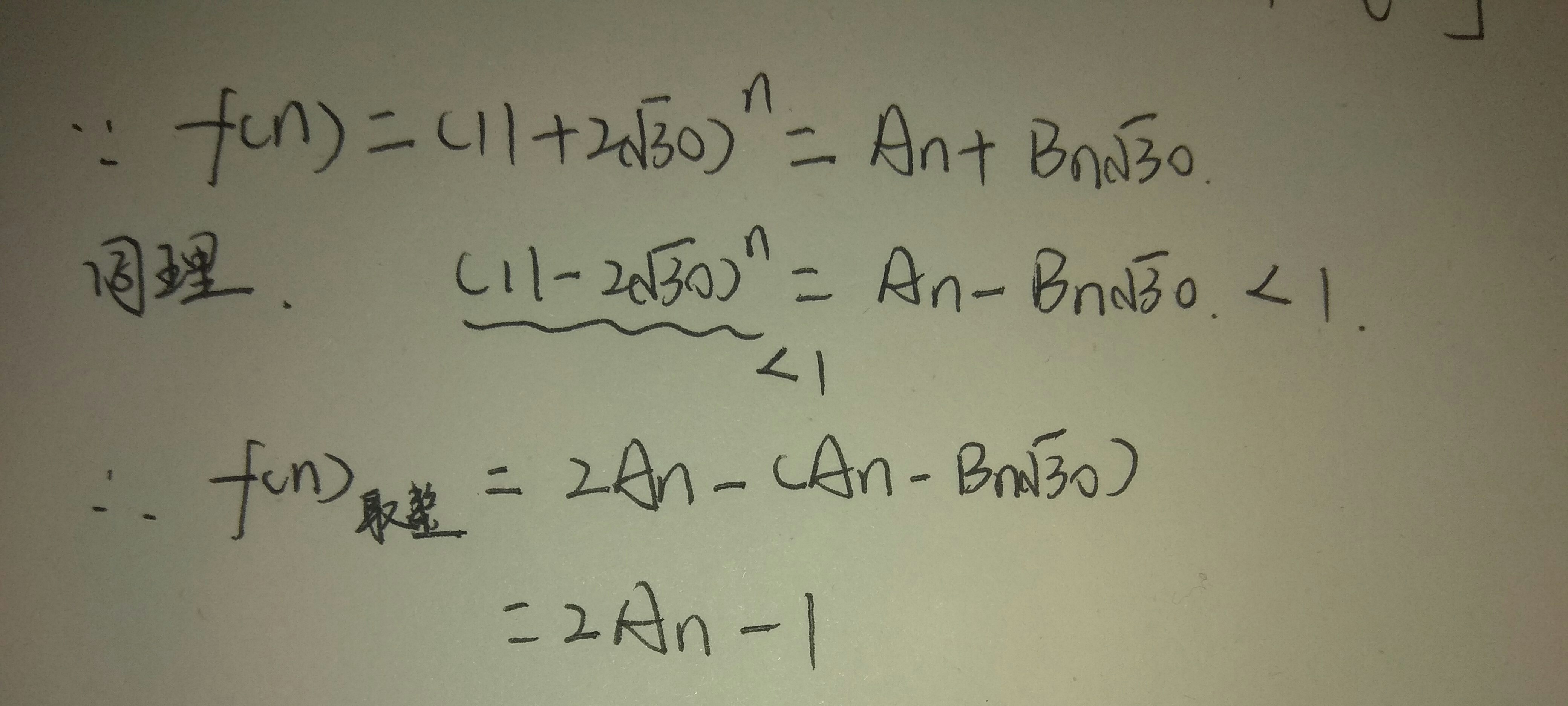
#include <iostream>
#include<string.h>
#include<stdio.h>
#include<math.h>
#define ll long long
using namespace std;
const ll mod = 9932017;
struct mat//定义矩阵结构体
{
  ll m[2][2];
  mat()
  {
    memset(m, 0, sizeof(m));
  }
};
mat mul(mat &A, mat &B)
{
  mat C;
  for (int i = 0; i < 2; i++)
  {
    for (int j = 0; j < 2; j++)
    {
      for (int k = 0; k < 2; k++) 
      {
        C.m[i][j] = (C.m[i][j] + A.m[i][k] * B.m[k][j]) % mod;
      }
    }
  }
  return C;
}
mat pow(mat A, ll n)
{
  mat B;
  for(int i=0;i<2;i++)//初始化方阵
    B.m[i][i]=0;

  //初始被乘矩阵的初值
  B.m[0][0]=11;
  B.m[1][0]=2;

  while (n)
  {
    if (n & 1)
      B = mul(A, B);//注意这里，矩阵的左乘和右乘是不一样的，对应的系数矩阵也不一样
    A = mul(A, A);
    n >>= 1;
  }
  return B;
}
int main()
{
  ll n,t;
  cin>>t;
  mat A;//矩阵A是系数矩阵（转移矩阵）
    A.m[0][0]=11;
    A.m[0][1]=60;
    A.m[1][0]=2;
    A.m[1][1]=11;
 for(int i=0;i<t;i++)
  {
    scanf("%lld",&n);//cin会超时
    if(n==0)
    {
      printf("1\n");
    }
    else if(n==1)
    {
      printf("21\n");
    }
    else
    {
      mat B = pow(A, n-1);
      printf("%lld\n",(2*B.m[0][0]-1)%mod);//2An-1
    }
   }
  return 0;
}