图论
多源最短路(在曼哈顿图中)(无例题)(使用BFS,队列):
操作的地图要有两个特点:既可以表示结果中所要的最短距离,又能记录这个点是否走过,那就全部memset为一个特殊的数-1(这里一定要专门设计一个结果图,不能只用最初的图,让最初的图承担三个责任,它哪里做的到啊(表示举例,判重,记录最初信息)(非要做的话,你可以想象,如果发现一个点可以是起点,那就改变其值为0,这个0要如何与其他没去过的点的0区分呢,如果另开一个数组那就可以区分了,起点处是0,没去过的地方是-1)),这就是个特殊的判重技巧:另开一个数组。
本题代码有个bug,不知道为什么输出结果有误,以后改过来。
题目:
code:
 View Code
View Codedijkstra算法解决单源最短路问题:
问题:给出一个有向图,请问图中某一个点(这个点记作源点)到其余各点的最短距离是多少?
思路:(基于贪心算法)
1.将所有点到源点的距离初始化为无穷大
2.找到图中目前为止距离源最近的点
3.更新这个点的所有邻点的距离(松弛操作)
4.反复2,3操作直到遍历所有点为止
时间复杂度:O(n^2+m)
缺点:不能找出带有负边权的图,不能解决带有负环的图
注:vector是一个什么样的数据结构呢?vector是一个动态数组,像vector <int>a;这样就已经创建了一个整型数组。
题目:洛谷P3371(终极代码,极限压行之24行解决问题)
#include <bits/stdc++.h> using namespace std; int n, m, s, dist[10005]; struct edge { int v; int w; }; const int inf = 2147483647; vector<edge>ed[10005]; bool visit[10005]; void dijkstra() { for (int i = 1; i < n; i++) { int u = 0; for (int i = 1; i <= n; i++)if (dist[i] < dist[u] && !visit[i])u = i; visit[u] = true; for (edge e : ed[u]) if (dist[e.v] > dist[u] + e.w)dist[e.v] = dist[u] + e.w; } } int main() { cin >> n >> m >> s; for (int i = 0; i <= n; i++)dist[i] = inf; dist[s] = 0; for (int i = 0; i < m; i++){ int u, v, w;cin >> u >> v >> w;ed[u].push_back({ v,w });} dijkstra(); for (int i = 1; i <= n; i++)cout << dist[i] << " "; return 0; }
dijkstra可以用堆来优化,得到heap-dijkstra算法
学会了dijkstra算法的堆优化,其实就是用一个小根堆来维护队列,将距离的相反数储存起来,这样堆顶的元素距离就最小(相反数最大)。
随后遍历每个点,已经遍历过的就打上visit标记不再遍历。题目:洛谷P4779.代码:
#include <bits/stdc++.h> using namespace std; int m,n,s,d[100005],visit[100005]; const long long inf=2147483647; struct edge{int v,w;}; priority_queue<pair<int,int>>q; vector <edge>ed[100005]; void heap_dijkstra(){ for(int i=1;i<=n;i++)d[i]=inf;//用不着0那个点喽! d[1]=0;q.push({0,1}); while(q.size()){ auto t=q.top(); q.pop(); int u=t.second; if(visit[u])continue; visit[u]=1; for(edge e:ed[u]){ int v=e.v,w=e.w; if(d[v]>w+d[u]){ d[v]=d[u]+w; q.push({-d[v],v}); } } } } int main(){ cin>>n>>m>>s; int a,b,c; for(int i=1;i<=m;i++){ cin>>a>>b>>c; ed[a].push_back({b,c}); } heap_dijkstra(); for(int i=1;i<=n;i++)cout<<d[i]<<' '; return 0; }
解析错误RE(runtime error):
1.数组开的小了,但题目数据规模大于数组的大小,所以根本给不出结果
2.数组开的太大了,系统根本给不出这么大的空间
3.除数是0
bellman-ford算法(单源最短路算法,比起dijkstra可以解决负边权问题):
问题:给出从一个点到其他点的最短距离,存在权值为负的边。
思路:
1.进行n轮判断
2.每轮判断中,对每条边都进行更新
3.如果某一轮没有再更新,那就停止判断
时间复杂度:一共n轮判断,每轮m条边,所以时间复杂度O(nm)
优点:可以判断负环
名词解释:什么是负环?
图中有一条路经过的边的权值之和是负数。这样一个图没有最短路,因为每走一遍这条路,权值都会变小。
如何用bellman-ford判断负环?
答:bellman-ford算法通过迭代算最短路径,每轮至少更新一个结点,最多更新n-1个结点,如果第n轮时发现仍有可以被更新的结点,那么存在负环。
题目:P3385
代码:
 View Code
View Code注:这个代码没过,而且不知道为啥过不去
bellman-ford算法优化算法: spfa(shortest path faster algorithm)(戏称shortest path fake algorithm)
考虑到在bellman-ford算法中每轮的判断其实不用考虑每一条边,只用考虑那些可能更新的边,所以开数组visit和队列q,visit用来标记点是否在队列内,相当于给队列加个扩展的小功能。在队列中进行大家习惯的更新操作。加一个cnt数组记录边数(某一条路径上经过了多少边)。
题目:P3385
背诵一个数字:2的32次方-1是21 47 48 36 47
生成树:
在一个连通图中,如果一个连通子图用n-1条边连接了全部N个点,这个连通子图就可以被称为生成树。
在一个带权图中,各边权值最小的生成树就是最小生成树。(MST,minimum spanning tree)
题目:洛谷P3366
#include <bits/stdc++.h> using namespace std; int n,m,res,visit[5005],d[5005],cnt; struct edge{int v,w;}; vector <edge> ed[5005]; #define inf 2147483647 int prim(){ d[1]=0; for(int i=1;i<=n;i++){ int u=0; //找最小点 for(int j=1;j<=n;j++) if(d[j]<d[u] && visit[j]==0)u=j; //找到了 visit[u]=1; //如果生成树中真的有新点加入 if(u!=0){ cnt++; res+=d[u]; } //更新整张图 for(edge e:ed[u]){ int v=e.v,w=e.w; if(d[v]>w)d[v]=w; } } //如果加入了n个点,那就有生成树,如果少于n那就i没有 return cnt==n; } int main(){ cin>>n>>m; int x,y,z; for(int i=0;i<=n;i++)d[i]=inf; for(int i=1;i<=m;i++){ cin>>x>>y>>z; ed[x].push_back({y,z}); ed[y].push_back({x,z}); } if(prim())cout<<res; else cout<<"orz"; return 0; }
寻找方法:PRIM算法,思想贪心。
全源最短路floyd算法(DP算法):(思想:动态规划,插点法)
1.遍历每个点作为插点
2.某个点作为插点时,更新从i到j的距离
图的储存方法:邻接矩阵法
优点:可以解决负权和负环问题。
void floyd() { for (int k = 1; k <= n; k++) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { d[i][j] = min(d[i][j], d[i][k] + d[k][j]); } } } }
最小环问题:使用floyd算法。
P6175
思路:插值,假设图中序号最大的点序号是k,k的邻居是i,j。看看i,k,j是不是最短路,不是的话就考虑下一个K。在此过程中用floyd算法不断更新i,j之间的距离备用。

#include <bits/stdc++.h> using namespace std; int n, m, d[105][105], w[105][105], res = 1e8;//因为初始值也需要相加,为了防止越界,我们用1e8,不用2147483647. bool floyd() { for (int k = 1; k <= n; k++) { for (int i = 1; i < k; i++) { for (int j = i+1; j < k; j++) {//j从i+1开始,是因为1->i-1的数都考虑过了,而考虑i到i显然是不合理的 res = min(res, w[i][k] + w[k][j] + d[i][j]);//0->k-1的距离都搞清楚了,涉及k的还不知道,所以用w这个代表真实距离的量 } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { d[i][j] = min(d[i][j], d[i][k] + d[k][j]); } } } return res != 1e8; } int main() { cin >> n >> m; for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)if (i != j)d[i][j] = w[i][j] = 1e8;//d代表最小距离 for (int i = 0; i < m; i++) {int x, y, z;cin >> x >> y >> z;d[x][y] = d[y][x] = w[x][y] = w[y][x] = z;}//w代表真实距离 if (floyd()) cout << res; else cout << "No solution."; return 0; }
最小生成树:
稠密图用prim,稀疏图用kruskal。
性质:代价唯一。
可能得到不同最小生成树的情况:网络中有权相同的边。若没有权相同的边,则不可能有不同的最小生成树。
题目:洛谷P3366.
思想:运用并查集与贪心算法求最小生成树
步骤:
1.初始化并查集,将n个点放入n个独立集合。
2.将每条边按照边权从小到大排序。
3.枚举每条边,如果边上的两个点不在同一个集合,那就合并起来并且加入最小生成树;如果在同一集合,那就跳过。
4.重复步骤3直到选取了n-1条边。如果不是连通图的话就选不了n-1条边。
复杂度:O(mlogm)(来自于排序sort)
这题过不了。。。。
lowest common ancestor最近公共祖先:
倍增算法:最经典的LCA算法。
预处理:
两个数组dep[u]结点u的深度,fa[u][i]结点u向上跳2的i层的祖先。
步骤:1.DFS求出两个数组,称为求ST表 2.在已经求好的ST表中求LCA,步骤有2,首先将u,v跳至同一层,其次将u和v跳至LCA的下一层
题目:洛谷P3379
最近公共组先tarjan(塔杨算法)算法:
#include<bits/stdc++.h> using namespace std; const int N=500005; vector<pair<int,int> >query[N]; vector<int>e[N]; int n,m,s,ans[N],visit[N],fa[N]; int find(int u){ if(u==fa[u])return u; return fa[u]=find(fa[u]); } void tarjan(int u){ visit[u]=true;//入 for(auto v:e[u]){ if(!visit[v]){ tarjan(v); fa[v]=u;//回 } } for(auto q:query[u]){//离 int v=q.first,i=q.second; if(visit[v])ans[i]=find(v); } } int main(int argc, char** argv) { cin>>n>>m>>s; for(int i=1;i<n;i++){ int x,y; cin>>x>>y; e[x].push_back(y); e[y].push_back[x]; } for(int i=1;i<=m;i++){ int x,y; cin>>x>>y; query[x].push_back({y,i}); query[y].push_back({x,i}); } for(int i=1;i<=n;i++)fa[i]=i; tarjan(s); for(int i=1;i<=s;i++)cout<<ans[i]<<" "; return 0; }
使用并查集进行离线(全部输入)计算。
在线计算:一般输入一边计算。
树剖算法写LCA:
洛谷3379:
算法复杂度:dfs1:O(n) dfs2:O(n) lca:O(mlog(n))(这是因为最多log(n)个重链) 一共O(n+mlog(n))
fa:父节点
son:重儿子
sz:该结点子树的结点数目
top:结点所在重链的根结点。轻儿子的根节点是它自己
dep:结点的深度
重儿子:子结点中sz最大的那个
轻儿子:除了重儿子之外的都是轻儿子
重链:重儿子们集合起来的链
三种算法比较:
倍增算法:最经典
tarjan:最高效
树剖:另有他用
DAG:有向无环图
AOV:activity on vertex network,用顶点表示活动的网络
我们往往用AOV或者DAG来表示一个大工程中各个小工程的前后顺序,而拓扑排序就是在AOV或DAG中找到一个可以正确施工的流程。
拓扑排序步骤:
1.将入度为0的点放入栈中
2.弹栈,将入度为0的点周围的邻点做处理:使邻点的入度减一,如果领点入度为0则入栈
反复执行第二步直到栈空
1.邻接矩阵法
时间复杂度==空间复杂度==O(n^2),建议用在点不多的稠密图中
2.邻接表
思想:
时间复杂度:O(n+m),原因:每个点都要遍历,总体来看每条边都要遍历;(无论DFS,BFS)
空间复杂度:O(n+m)。时间复杂度大大降低,但可惜不能处理反向边。
3.十字链表
思路:邻接矩阵和逆邻接矩阵相结合。
空间:O(n+m),需要2*m+2*n个指针。
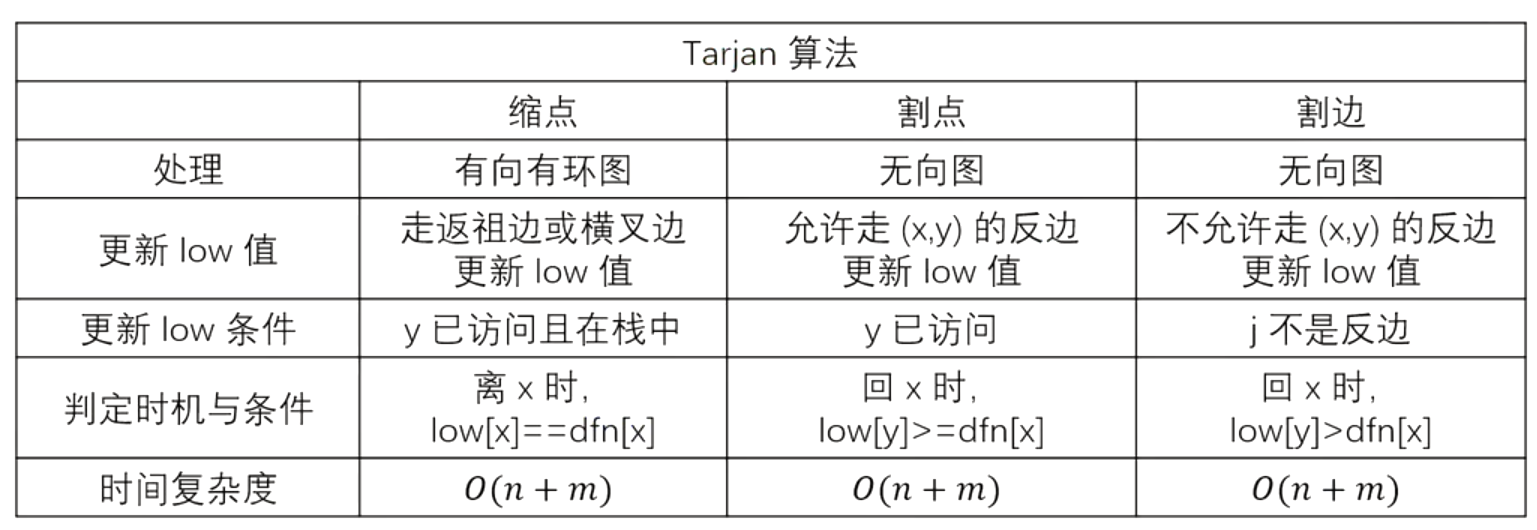
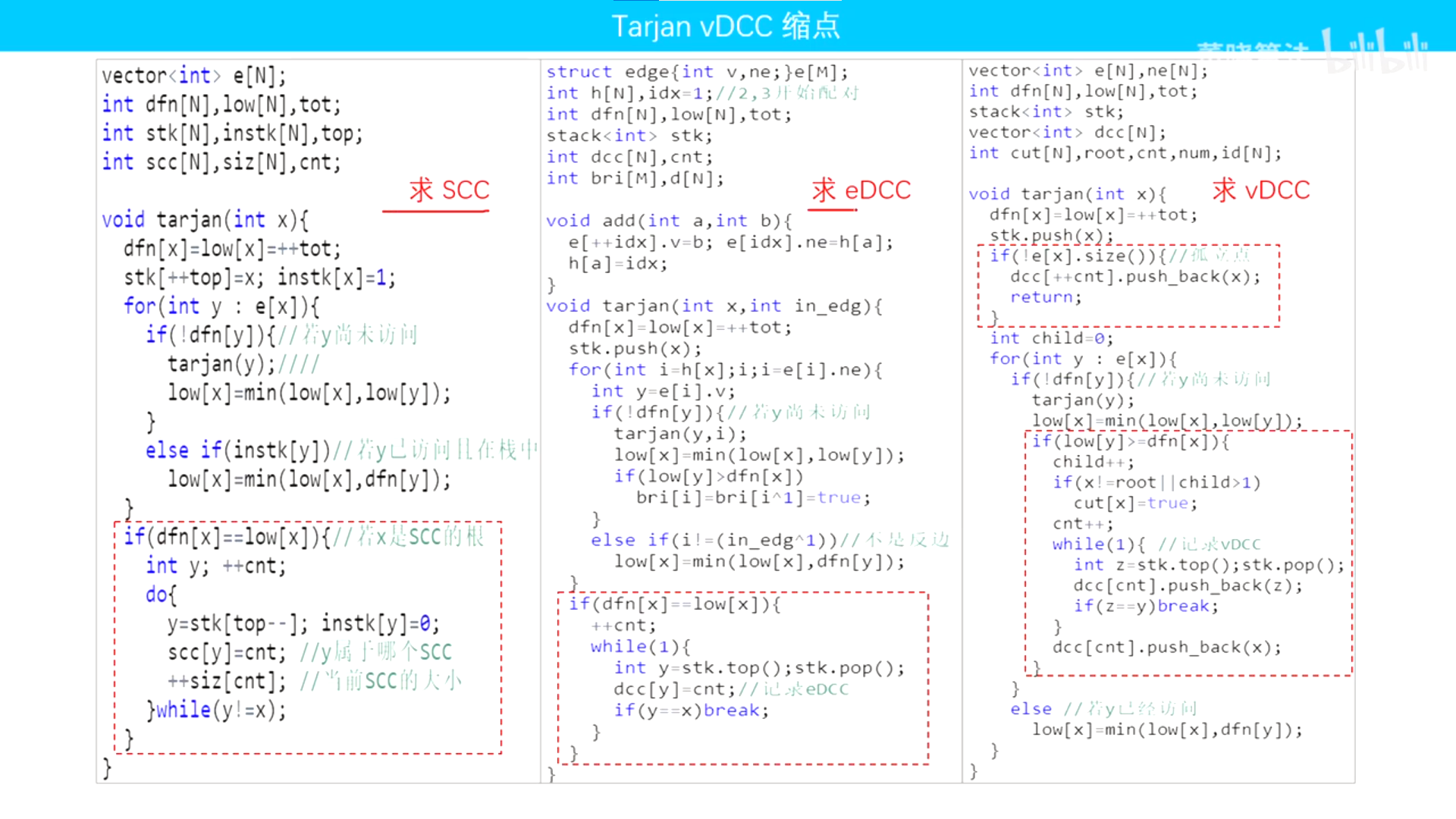
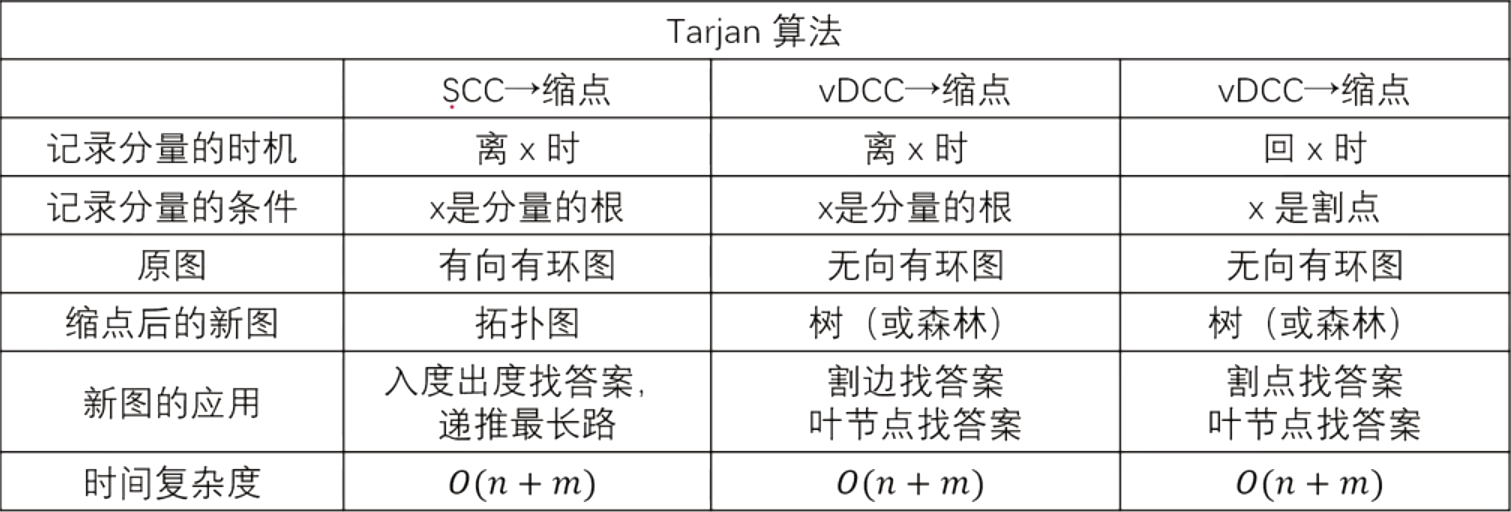
连通性问题(用tarjan算法在有向图,无向图中进行求强连通分量,缩点,找割点,找割边等操作):
基础概念+在有向图中缩点+在无向图中找割点+在无向图中找割边





割边:P1656
//c/c++ compile run 插件中设置external terminnal,f6运行 #include <iostream> #include <vector> #include <algorithm> using namespace std; const int N = 160; const int M = 5010; int n, m, dfn[N], low[N], tot, cnt;//cnt 表示割边的序号,tot表示点的序号 struct edge{int u, v;}; vector<int>h[N];// 出边 vector<edge>e;// 图 edge bri[M]; void add(int a,int b){ e.push_back({a,b}); h[a].push_back(e.size()-1); } void tarjan(int u,int in_edg){ dfn[u] = low[u] = ++tot; for(int i = 0;i < h[u].size();i ++){ int j = h[u][i], v = e[j].v; if(!dfn[v]){ tarjan(v, j); low[u]=min(low[u],low[v]); if(low[v]>dfn[u]){ bri[++cnt]=e[j]; } }else if(j != (in_edg^1)){// 这条边不是反边 low[u]=min(low[u],dfn[v]); } } } bool cmp(edge a,edge b){ if(a.u < b.u)return true; if(a.u > b.u)return false; if(a.v < b.v)return true; return false; } int main(){ cin.tie(0); cin.sync_with_stdio(false); cin >> n >> m; while(m--){ int a, b; cin >> a >> b; add(a,b);add(b,a); } for(int i = 1;i<=n;i++)if(!dfn[i])tarjan(i,0); sort(bri+1,bri+1+cnt,cmp); for(int i=1;i<=cnt;i++){ cout << bri[i].u << ' ' << bri[i].v << endl; } return 0; }
边双连通分量:(此处用到链式前向星来储存图)POJ3177题
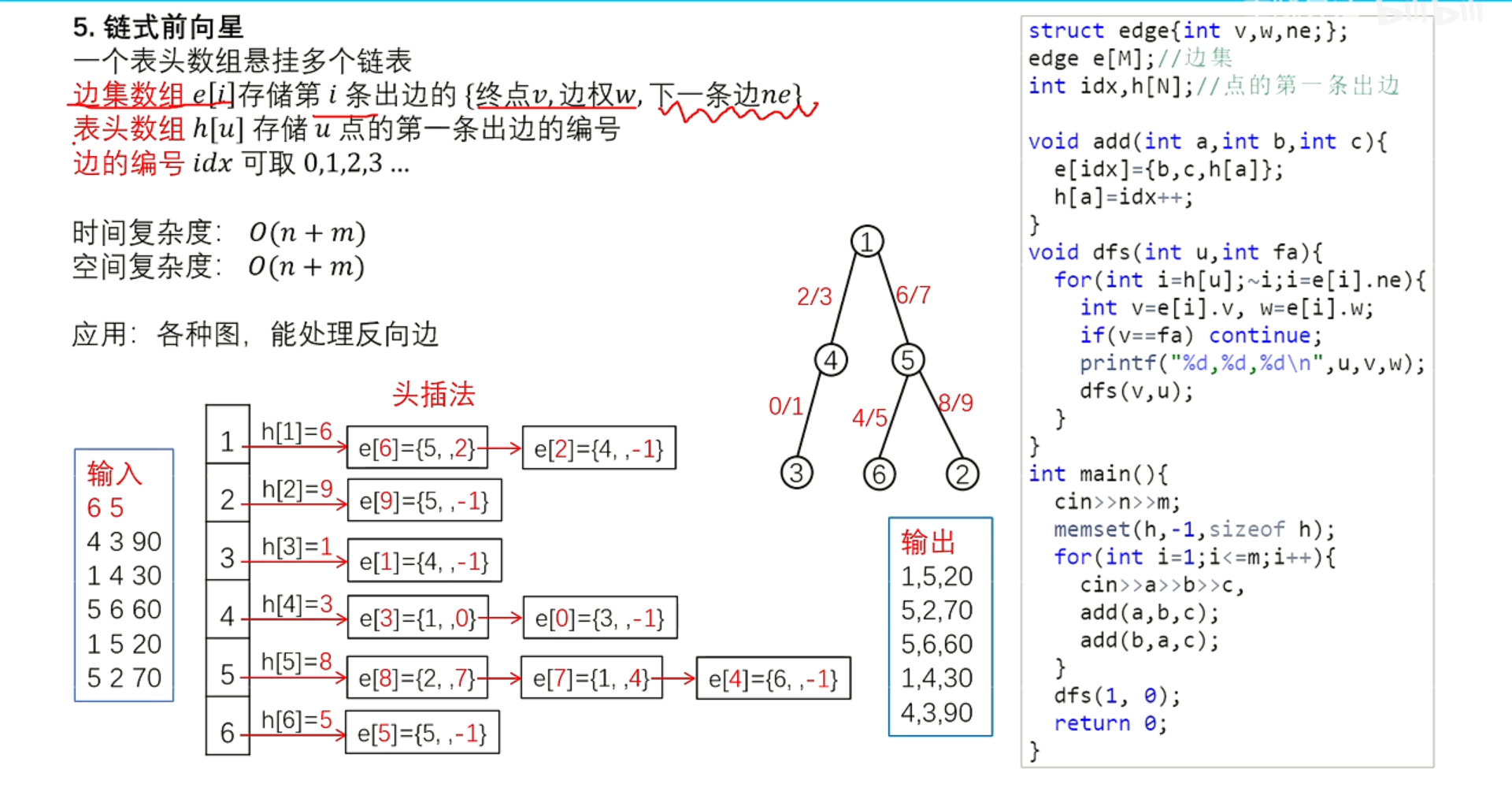
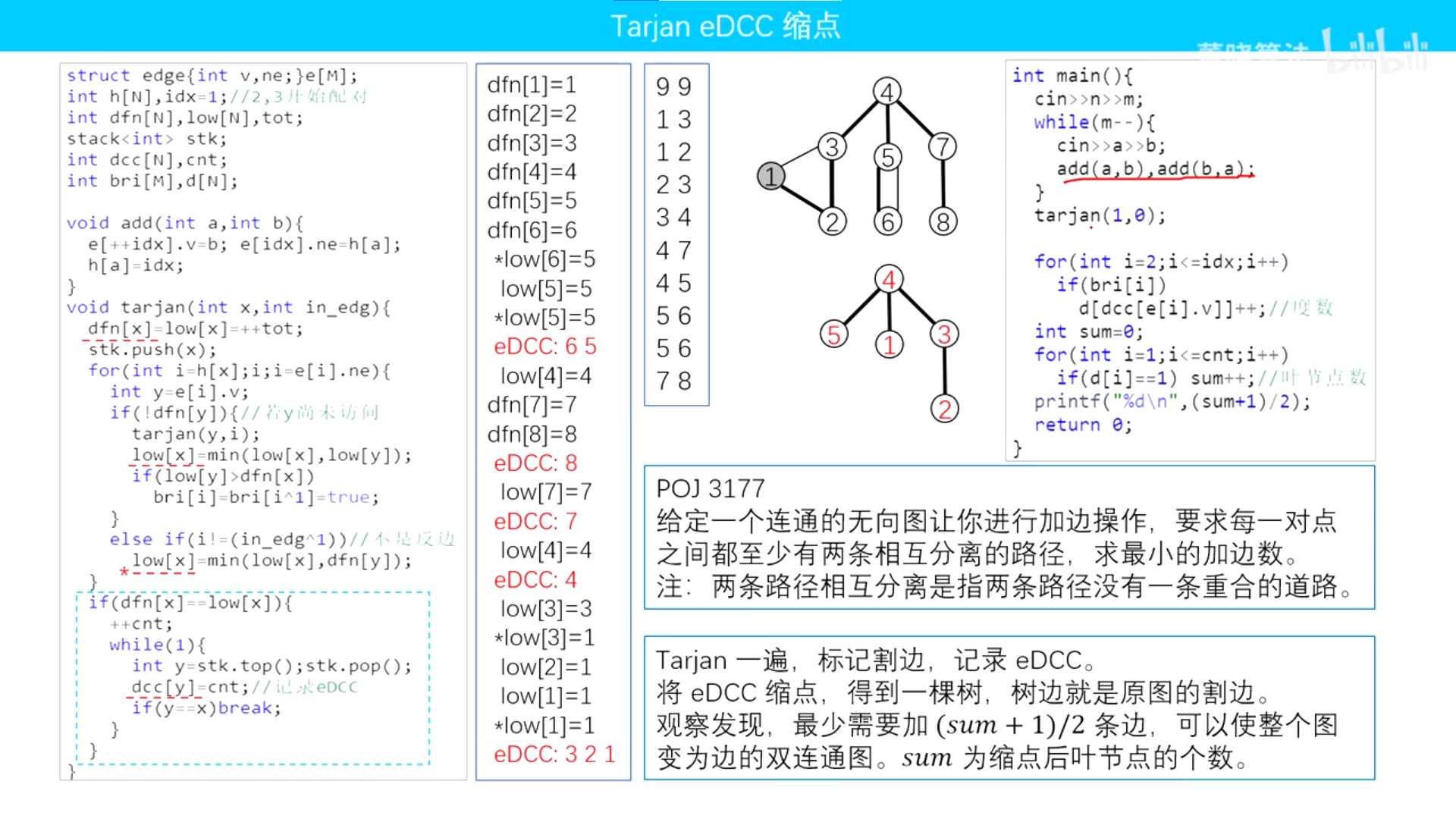
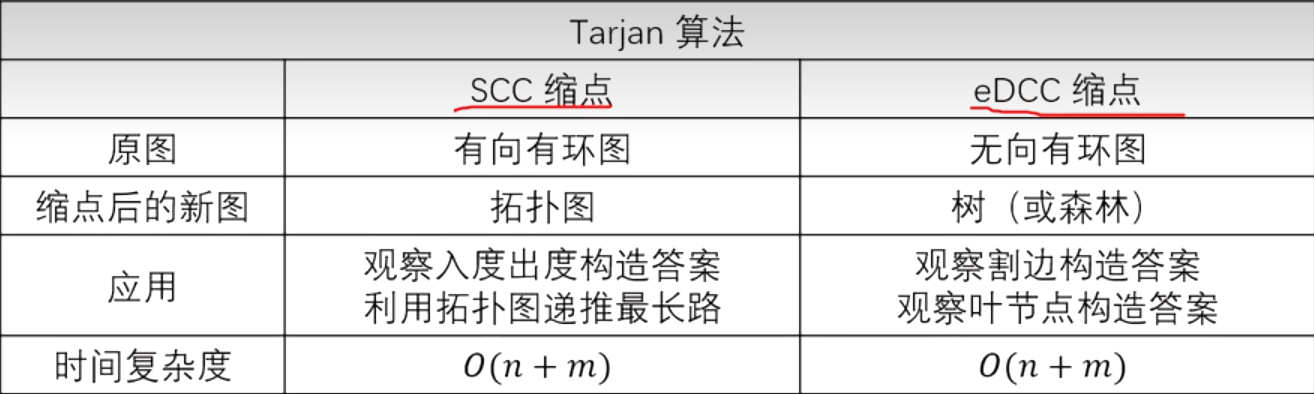
//c/c++ compile run 插件中设置external terminnal,f6运行 #include <iostream> // 无向图 #include <vector> using namespace std; const int N = 5005; const int M = 100005; struct edge{int v,ne;}e[M]; // 链式前向星 int h[N],idx=1; // 从2开始计数 int dfn[N], low[N], tot; int stk[N], top; int dcc[N], cnt; // 双连通分量 int d[N]; // 度数 bool bri[N]; // 是否桥 int n, m, a, b; // 点数,边数 void add(int u,int v){ e[++idx].v = v;// 进行头插法 e[idx].ne = h[u]; h[u] = idx; } void tarjan(int u,int in_edg){ low[u] = dfn[u] = ++tot; stk[++top] = u; for(int i=h[u];i;i=e[i].ne){ int v = e[i].v; if(!dfn[v]){ tarjan(v, i); low[u] = min(low[u],low[v]); if(low[v]>dfn[u]){ bri[i]=bri[i^1]=true; } }else if(i != (in_edg^1)){ low[u]=min(low[u],dfn[v]); } } if(dfn[u]==low[u]){ ++cnt; while(1){ int y=stk[top--]; dcc[y]=cnt; if(y==u)break; } } } int main(){ cin.tie(0); cin.sync_with_stdio(false); cin >> n >> m; while(m--){ cin >> a >> b; add(a,b); add(b,a); } tarjan(1,0); for(int i=2;i<=idx;i++) if(bri[i]) d[dcc[e[i].v]]++; int sum = 0;// 叶子节点个数 for(int i=1;i<=cnt;i++)if(d[i]==1)sum++; printf("%d",(sum+1)/2); return 0; }
求解点双连通分量:

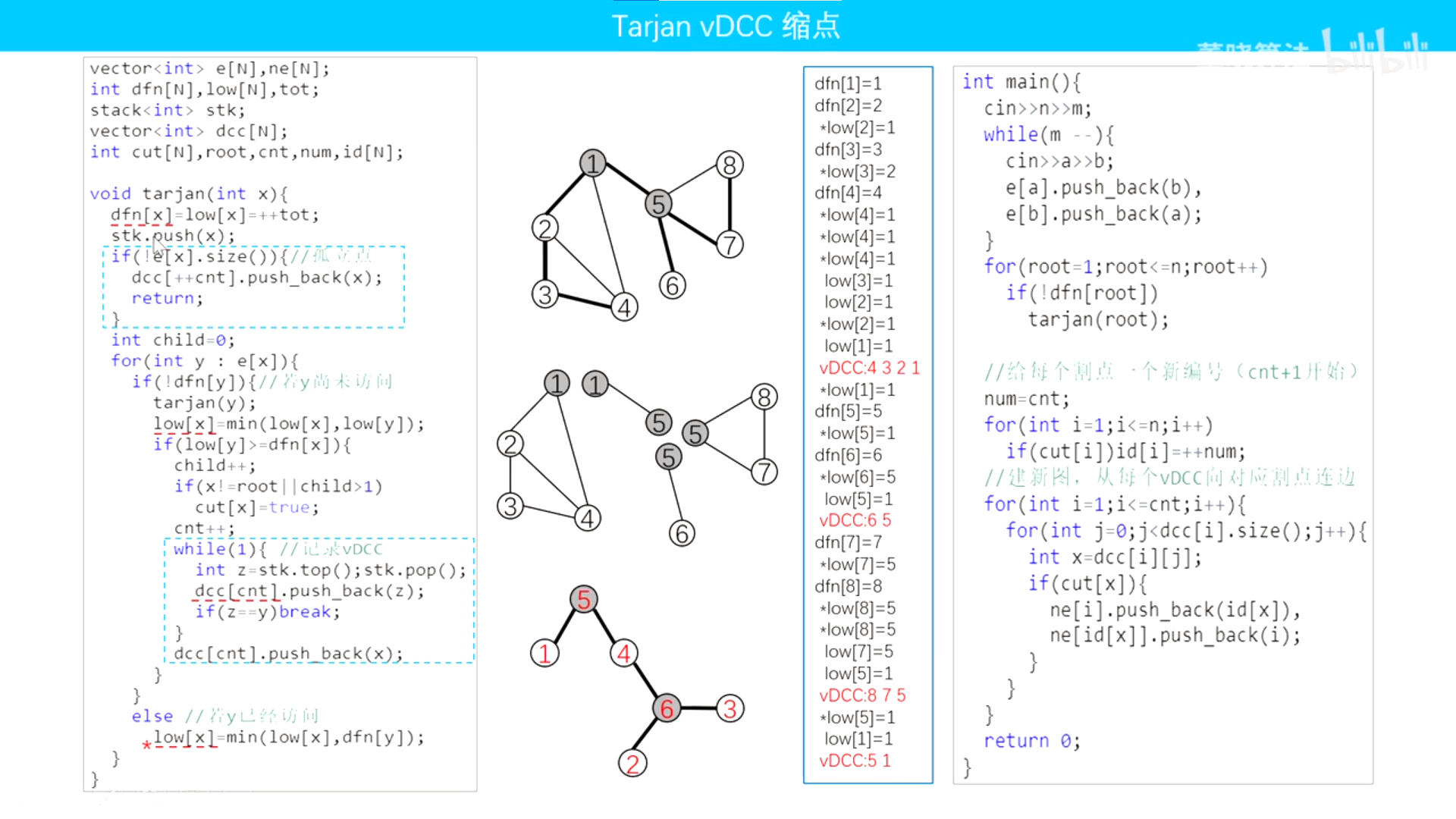
P2272:这紫题就是不一般,写了一天没写出来,焯!
//c/c++ compile run 插件中设置external terminnal,f6运行 // 建立的新图中可能会有重边,记得去重!好坑啊! #include <iostream> #include <vector> using namespace std; const int N = 100005; vector<int>e[N], ne[N]; //ne是新图,表示各个连通块 int scc[N], siz[N], cnt; int stk[N], top; bool in_stk[N]; int low[N], dfn[N], tot; int n, m, p, a, b; int num[N], again[N]; // num[u]记录从u这个连通块出发的最长路径(包括路径上连通块内的节点个数);again[u]表示u这个联通块的最长路径有几条 int dfs(int u){ // 以u为起点的路径有多长 if(num[u])return num[u]; num[u]=siz[u]; int temp=0; again[u]=1;//如果一个块没有相邻节点,那就只用一次 for(int v=0;v<ne[u].size();v++)if(dfs(ne[u][v])>temp)temp=num[ne[u][v]],again[u]=1;else if(num[ne[u][v]]==temp)again[u]++; num[u]+=temp; return num[u]; } void tarjan(int u){ in_stk[u]=true;stk[++top]=u;low[u]=dfn[u]=++tot; for(int i=0;i<e[u].size();i++){ int v=e[u][i]; if(!dfn[v]){ tarjan(v); low[u]=min(low[u],low[v]); }else if(in_stk[v]){ low[u]=min(low[u],dfn[v]); } } if(low[u]==dfn[u]){ int v;cnt++; do{ v=stk[top--];in_stk[v]=false; scc[v]=cnt,siz[cnt]++; }while(v!=u); } } int main(){ cin.tie(0); cin.sync_with_stdio(false); cin >> n >> m >> p; while(m--){ cin >> a >> b; e[a].push_back(b); } for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i); for(int i=1;i<=n;i++){ for(int j:e[i]){ if(scc[i]!=scc[j]){ bool flag=false;// 不存在重边 for(int k:ne[scc[i]]){ if(k==scc[j]){flag=true;break;} } if(flag==false)ne[scc[i]].push_back(scc[j]); } } } int res=0,how_many=0; for(int i=1;i<=cnt;i++)if(dfs(i)>res)res=num[i],how_many=again[i];else if(num[i]==res)how_many+=again[i]; cout<<res<<endl<<how_many%p; return 0; }
灵活运用割点理论:P5058
注:此处割点必须在a,b之间;所以只要满足在a,b之间即可,对tarjan算法进行改动;

//c/c++ compile run 插件中设置external terminnal,f6运行 #include <iostream> #include <vector> using namespace std; const int N = 200005; vector<int>e[N]; int scc[N], siz[N], cnt; bool cut[N]; int low[N], dfn[N], tot; int n, a, b; void tarjan(int u){ low[u]=dfn[u]=++tot; for(int v:e[u]){ if(!dfn[v]){ tarjan(v); low[u]=min(low[u],low[v]); if(low[v]>=dfn[u]&&u!=a&&dfn[b]>=dfn[v]){ cut[u]=true; } }else{ low[u]=min(low[u],dfn[v]); } } } int main(){ cin.tie(0); cin.sync_with_stdio(false); cin>>n; while(true){ cin>>a>>b; if(!(a==0&&b==0)){ e[a].push_back(b); e[b].push_back(a); }else break; } cin>>a>>b; tarjan(a); for(int i=1;i<=n;i++)if(cut[i]){ cout<<i; return 0; } cout<<"No solution"; return 0; }
割点模板P3388:

#include <iostream> #include <vector> using namespace std; const int N = 20005; vector<int> e[N]; int n, m, root, a, b; bool cut[N]; int dfn[N], low[N], tot; void tarjan(int x){ dfn[x] = low[x] = ++tot; int child = 0; for(int y:e[x]){ if(!dfn[y]){ tarjan(y); low[x] = min(low[x], low[y]); if(low[y] >= dfn[x]){ child ++; if(child > 1 || x != root){ cut[x] = true; } } }else low[x] = min(low[x], dfn[y]); } } int main(){ cin.tie(0); cin.sync_with_stdio(false); cin >> n >> m; for(int i = 1;i <= m;i ++){ cin >> a >> b; e[a].push_back(b); e[b].push_back(a); } for(root = 1;root <= n;root ++)if(!dfn[root])tarjan(root); int res = 0; for(int i = 1;i <= n;i ++)if(cut[i])res++; cout << res << endl; for(int i = 1;i <= n;i ++)if(cut[i])cout<<i<<' '; return 0; }
hamilton模板:

#include<bits/stdc++.h> using namespace std; const int N=21; int n,a[N][N],dp[1<<N-1][N]; int hamilton(){ int res=2147483647; memset(dp,0x3f,sizeof dp); dp[1][1]=0; for(int i=1;i<(1<<n);i++){//i表示状态 for(int j=1;j<=n;j++){//j表示终点 if(i>>j-1&1)//i能到j for(int k=1;k<=n;k++){//k表示中间点 if(i>>k-1&1){//i能到k dp[i][j]=min(dp[i][j],dp[i-(1<<j-1)][k]+a[k][j]); } } } } for(int i=1;i<=n;i++){ res=min(res,dp[(1<<n)-1][i]); } return res; } int main(){ cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j]; cout<<hamilton();//最短hamilton路径长度 return 0; }


