Codeforces Round #709 (Div. 1, based on Technocup 2021 Final Round) 题解

A - Basic Diplomacy

Solution 1

贪心，贪法可能有很多，这里讲一种。首先选出出现天数最多的人 \(x\)，记出现了 \(k\) 次。那么：

• 如果 \(k\le \lceil m/2\rceil\)，那么每天都能随便填。很显然最大的都不超过一半，那么所有都不超过一半。
• 如果 \(k\ge \lceil m/2\rceil\)，那么先填 \(\lceil m/2\rceil\) 个 \(x\)，然后剩下随便填，注意 \(x\) 优先先往只能填 \(x\) 的地方填。填完后天数不超过一半。

Solution 2

发现这是个二分图，建个图可以大力流，Dinic 应该就行了。

实际上这个做法更具普遍性，可以应付不一定为 \(\lceil m/2\rceil\) 的情况，然而没上面好写。

B - Playlist

先扫一遍找出所有可能会发生删除的位置，即相邻两个 \(\gcd = 1\) 的。用个 std::set 之类的维护一下。然后按位置顺序做过去。每次删除 \(x\) 之后，即 \(x\) 原前驱后继分别为 \(a, b\)，那么由于 \(x\) 的删除是因为 \(a\)，于是原本 \(b\) 可能因为 \(x\) 被删，现在不可能了，那么应该用 \(a\) 取代 \(x\) 的位置然后更新。

然后特判 \(1\)，因为 \(\gcd(1, x)=1\)，\(\forall x\ge 1\)。最后我这种的时间复杂度为 \(O(n\log n)\)，也许可以线性。

C - Skyline Photo

naive 的 dp 式子十分显然：\(f_i = \max_{j<i} \{f_j + \text{beauty}(j+1,i)\}\)，其中 \(f_i\) 表示前 \(i\) 个的答案，\(\text{beauty}(l, r)\) 表示区间 \([l,r]\) 的“美丽度”。

考虑由 \(i\to i+1\) 后 \(\text{beauty}\) 的变化。设 \(L_i\) 为满足 \(a_k<a_k\) 的最大的 \(k\)。那么只有 \((L_i, i]\) 的位置会被覆盖。发现这好像是一整个区间干同一个事情，尝试使用线段树优化。

对于位置 \(i\)，我们维护 \(f_i+\text{beauty}(i+1, cur)\) 的值，其中 \(cur\) 表示现在要求 \(f_{cur}\)。在求 \(f_{cur}\) 前，先消去 \((L_{cur}, cur)\) 中前几个 \(\text{beauty}\) 的影响（区间减），然后加上当前的 \(b_{cur}\)（区间加）。最后统计 \([0, i)\) 的最大值（区间最值）。

然后单调栈求出 \(L_i\) 就做完啦，复杂度 \(O(n\log n)\)。

D - Useful Edges

先膜万老爷 @OIerwanhong。

对于一条限制 \((s, t, l_{s,t})\) 和一条边 \((u, v, w_{u,v})\)，可以写出合法的条件是：

\[d(s,u)+w_{u,v}+d(v,t)\le l_{s,t} \]

我们发现对于左侧的枚举大概要 \(O(n^4)\)，因为有四个变量。于是移项得：

\[d(s,u)+w_{u,v}\le l_{s,t}-d(v,t) \]

那么对于一组 \((s,u)\)，对答案的贡献即为满足 \(d(s,u)+w_{u,v} \le \max_{t}\{l_{s,t}-d(v,t)\}\) 的 \(v\) 个数。然而这个式子两边可以分开，具体而言设 \(c(s, v) = \max_{t}\{l_{s,t}-d(v,t)\}\)，于是乎只要枚举 \((s,u)\)，再枚举 \(v\) 就可以了。然后（包括计算 \(c\) 显然也是）复杂度 \(O(n^3)\)。

E - Vabank

有点像“扔鸡蛋”的问题，看了题解大致有了个数。

首先把题目说得模糊一点，就是：一次询问，如果成功了那么“机会”加一，反正减一。这样虽然模糊，因为每次执行一次测试可能会消耗一次额外的询问作为成本。但感谢理解一下，这个额外的成本会下降的很快（实践证明 \(\approx 3\)），所以还是有点靠谱的。

算法的第一步是倍增找到第一个 \(x\) 使得答案 \(M\) 在 \([2^{x-1}, 2^x)\) 之间。一般我们做二分答案题都是直接二分，但这里一次询问需要一段“安全区间”作为每次测试的成本，这里的 \(2^{x-1}\) 就是最大我们可以的获取成本。

然后开始二分……吗？如果我们中间的切点取得太靠近左端点，可能试的效率不太行；而太靠近右端点就会罚 时 款吃到饱。

于是就有一个 非常不自然的 dp，和扔鸡蛋类似，设 \(f(i,j)\) 表示通过 \(i\) 次询问，\(j\) 次机会（见上），可以解决的答案的规模最大是多少。那么有：\(f(i,j) = f(i-1,j-1)+f(i-1,j+1)+1\)，即不管这一次测试的成功与否，我们都可以排除掉一部分可能的答案区间，锁定另一半区间，本质上是同时得到了两侧区间的信息，\(+1\) 则表示当前点也被判定了。初始条件：\(\forall j\ge 0:f(0,j)=0\)。

然后我们的中间点根据 \(f\) 这个 dp 数组确定就行了。具体而言，设 \([l,r]\) 为二分到的当前区间，那么我们先减少 \(f(i,j)\) 中的 \(i\) 使得 \(f(i,j)\) 的大小在区间长度范围内，然后直接切 \(l+f(i,j)\) 的位置，当然在这之前可能要先花几次询问补充成本，每次成功的询问都对应一个机会的加一，反之即为减一。

实测 98 max queries participant，非常靠谱。

F - Exam

参考代码：https://strncmp.blog.luogu.org/editorial-cf1483f

想复杂了，实际上是道并没有多难的题。

先考虑没有第三条限制的情况。这个比较简单：先对所有串建立 AC 自动机并整出 fail 树，然后对于每个串在自动机上跑一遍，树状数组随便维护一下就行。

然后思考第三条限制在何时会起作用。对于当前串 \(s_i\)，考虑到一个可以作为其子串的 \(s_j\) 时，假如存在一个 \(s_k\) 使得 \(s_k\) 在 \(s_i\) 上覆盖到的区间将 \(s_j\) 完全包含，那么 \(s_j\leftrightarrow s_i\) 之间的贡献就不能被记入答案。并且在所有出现的位置中，有一个存在这样的情况就不行。如果没有出现，并不代表 \(s_j\) 就一定不是 \(s_k\) 的子串，仅仅是在 \(s_i\) 中没有体现而已。但这样在 \(s_j\leftrightarrow s_i\) 没有体现，那么就不会像第三条限制那样夹在中间。

首先对于 fail 树中的每个结点，多维护一个 trans[x]，表示 \(x\) 最近的可以表示一个整串的对应字符串的编号。由于跳 fail 链就是找最长真后缀，再找下去一定不符合限制 3。

那么枚举 \(s_i\) 的前缀，从长到短，然后维护一个字段 min_sp 表示先前匹配到的字符串中，左端点最靠左的左端点。这时“包含”即为，当前前缀的最长匹配到其他串的后缀，对应的起始点反而在更后侧的前缀匹配到的 min_sp 的后面。

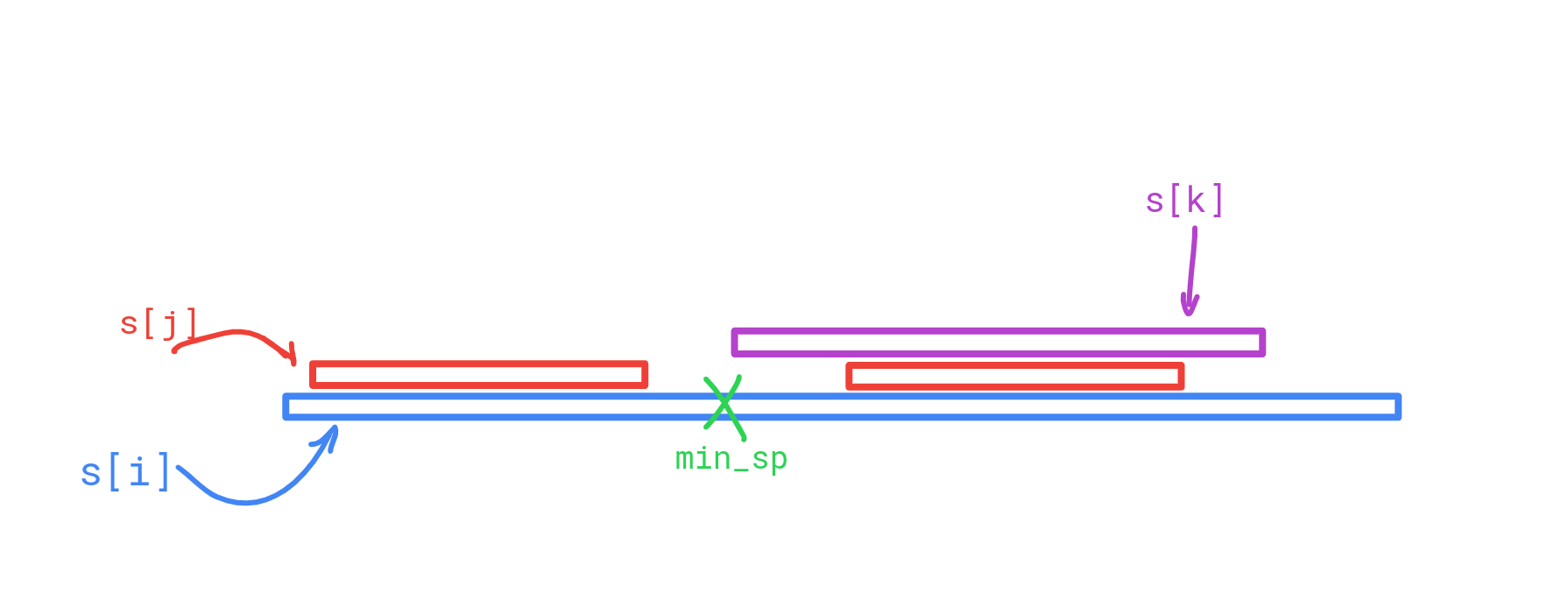
再维护一个计数器 cnt[]，仅当匹配到的左端点 < min_sp 时更新。已经很显然了：只有计数器 cnt 的值恰好等于其在 \(s_i\) 中的出现次数时答案 +1。出现次数可以用常规的 dfs 序 + 树状数组维护。

时间复杂度 \(O(n\log n)\)。