K-D tree 区域查询复杂度证明

查询算法的流程

• 如果查询与当前结点的区域无交集，直接跳出。
• 如果查询将当前结点的区域包含，直接跳出并上传答案。
• 有交集但不包含，继续递归求解。

K-D Tree 如何划分区域

可以借助下文图片理解。

我们不仅可以将 K-D Tree 理解为一个高维二叉搜索树，通过某一维标准值进行元素的划分。

还可以理解为使用一些直线（线段或射线）将整个空间划分为若干个区域，便于缩小搜索范围，以达到剪枝的目的。

2-D 查询复杂度证明

有问题请在评论区指出，谢谢！

可以知道，时间开销最大的地方在于流程中“有交集但不包含”情况的处理。设这样的点的个数为 \(x\)，那么查询一次的时间复杂度为 \(O(x)\)

我们先放张图，假定查询是一个竖直线（询问区域在左边）：

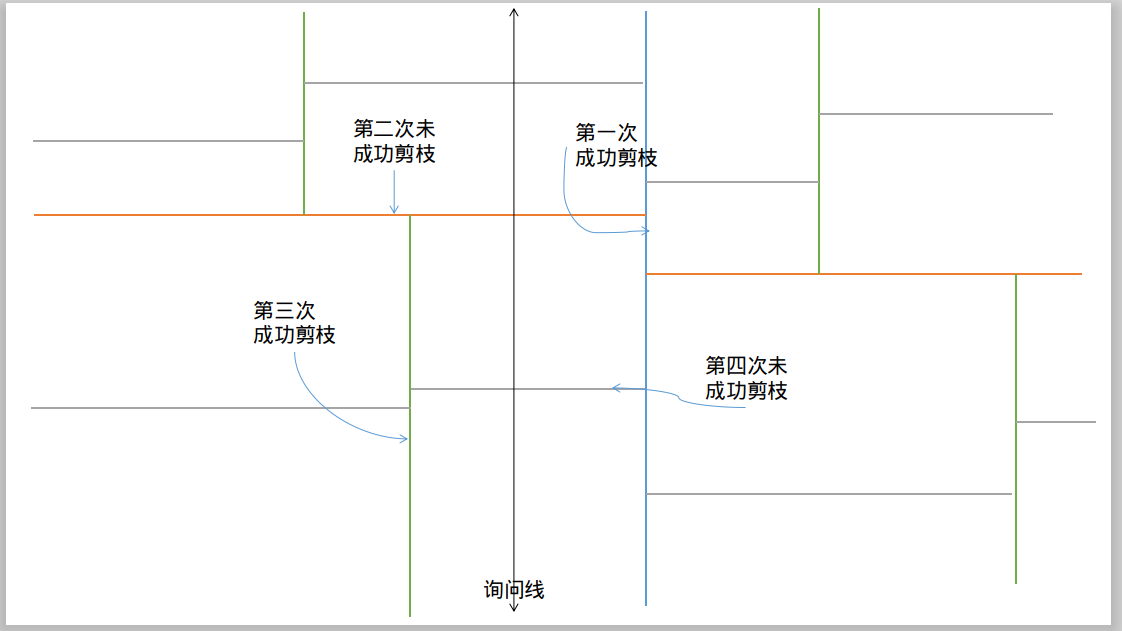
可以清晰地看见 K-D Tree 如何划分区域的：根结点、直接儿子、第三代子孙、第四代……，它们分别交替着划分第一维，第二维。

直接去考虑 \(x\) 的规模大小并不容易，不如尝试着研究它的剪枝情况。

首先，第一次我们的剪枝是有效的，右侧一半会被剪掉，那么往下结点数不翻倍。

首先，第二次我们的剪枝是无效的，那么往下结点数翻倍。

第三次有效，第四次无效……

这样一来，只有奇数层会有剪枝效果，偶数曾则没有。一颗 \(h\) 层的 K-D Tree，有 \(\frac{h}{2}\) 次翻倍，因此 \(x \approx \sum_{i=0}^{\frac{h}{2}} 2^i \approx 2^{\frac{h}{2}}\)。

由于带有替罪羊重构的 K-D Tree 是平衡的，那么 \(h \approx \log_2 n\)。

于是 \(x\approx 2^{\frac{h}{2}} = (2^{\log_2 n})^{0.5} = n^{0.5}\)

所以一次矩形查询的复杂度为 \(O(\sqrt{n})\)。

最后放张图，其中灰色结点是搜索范围（原图出处）：

K-D 查询复杂度证明

我们不难将 2-D 的证明推广之 \(k\) 维。

那么只有在 \(k\) 维中的一维才会有剪枝效果，其他维度结点都会 \(\times 2\)。

那么 \(\Large x \approx \sum\limits_{i=1}^{\frac{h(k-1)}{k}} 2^i \approx 2^{\frac{h(k-1)}{k}}\)。其中 \(h \approx \log_2 n\) 为树高。

\(\Large x \approx 2^{\frac{h(k-1)}{k}} = (2^{\log_2 n})^\frac{k-1}{k} = n^{\frac{k-1}{k}}\)。

由于还有一次 \(k\) 个维度的比较，那么一次就是 \(\Large O(k\cdot n^{\frac{k-1}{k}})\) 的时间复杂度。

后记

证明过程可能不是很严谨，有问题请指出。

reference：l1ll5 - K-D tree在信息学竞赛中的我也不知道有什么的应用

• 原文地址：https://www.cnblogs.com/-Wallace-/p/13429463.html
• 本文作者：@-Wallace-
• 转载请附上出处。