雨天的尾巴[树剖做法
树剖模板部分
还是树剖,今天本身想学线段树合并可惜我没学会,然后看到一道线段树合并的例题雨天的尾巴然后看到是树上一段路径的处理,就想到了树链剖分。具体怎么做还是不会看完题解只能理解树链剖分就写了树链剖分。
完整代码会放在结尾。
题目大意:
给定一珂n个点的树,m次操作,每次给出x y z,意思是x到y的路径上,所有点都获得一个编号为z的物品,m次操作后,问你每一个点最多的物品 的编号[比如一个点,被发过的物品有 1 2 2 2,那么最多的物品编号就是2]。
对于路径操作自然想到了树链剖分,画一棵树[就是样例里面的那棵],重儿子用红色标记[3的重儿子是5是因为这条边后加,前向星里会是第一条,第一个被访问到,所以虽然 4 5大小一样,5是重儿子,对着代码模拟模拟就能看出来]
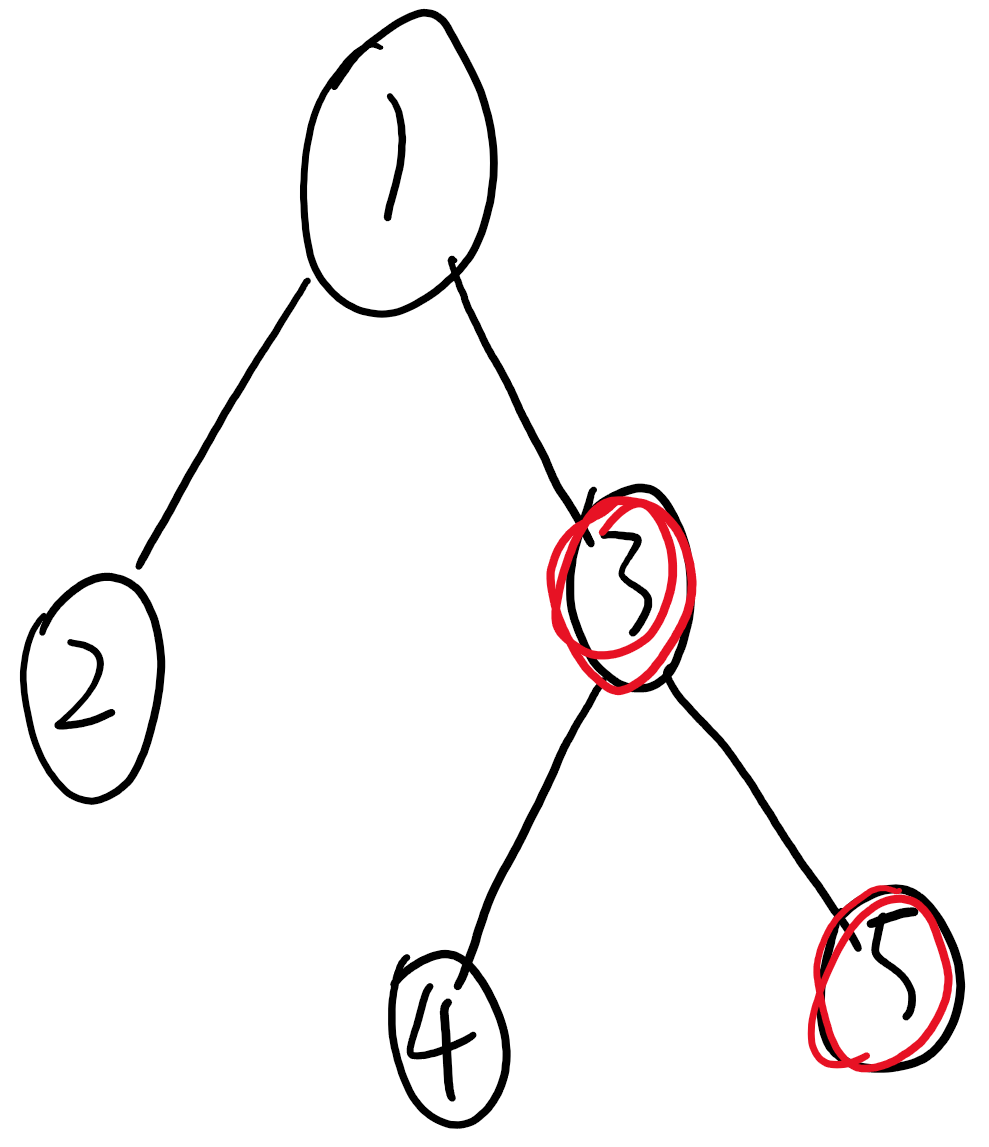
然后我们就可以求重链,将树变成一个序列。
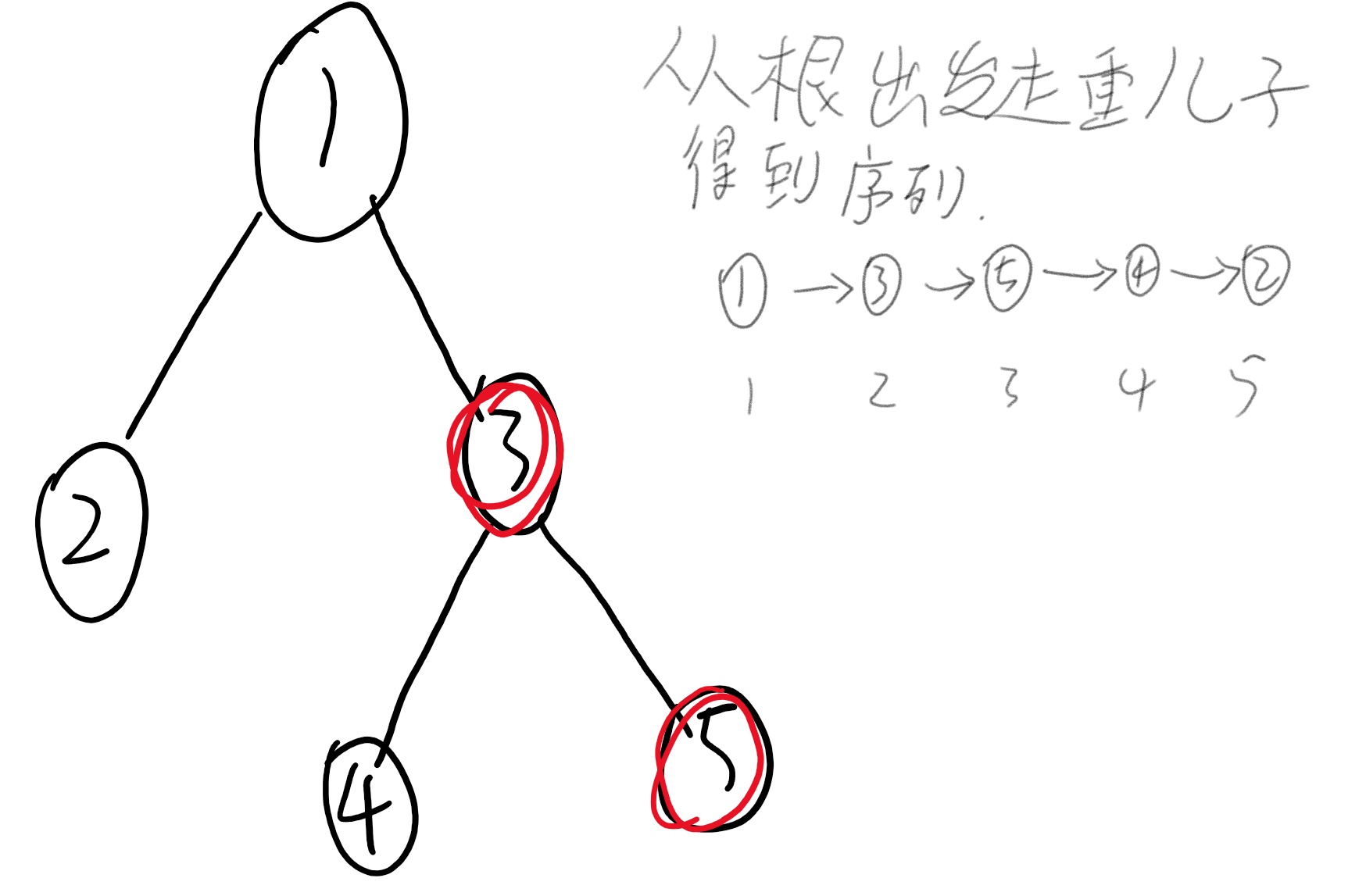
那么原先在树上的操作就可以变成在序列上,那怎么操作呢?我们看一下样例有什么操作。
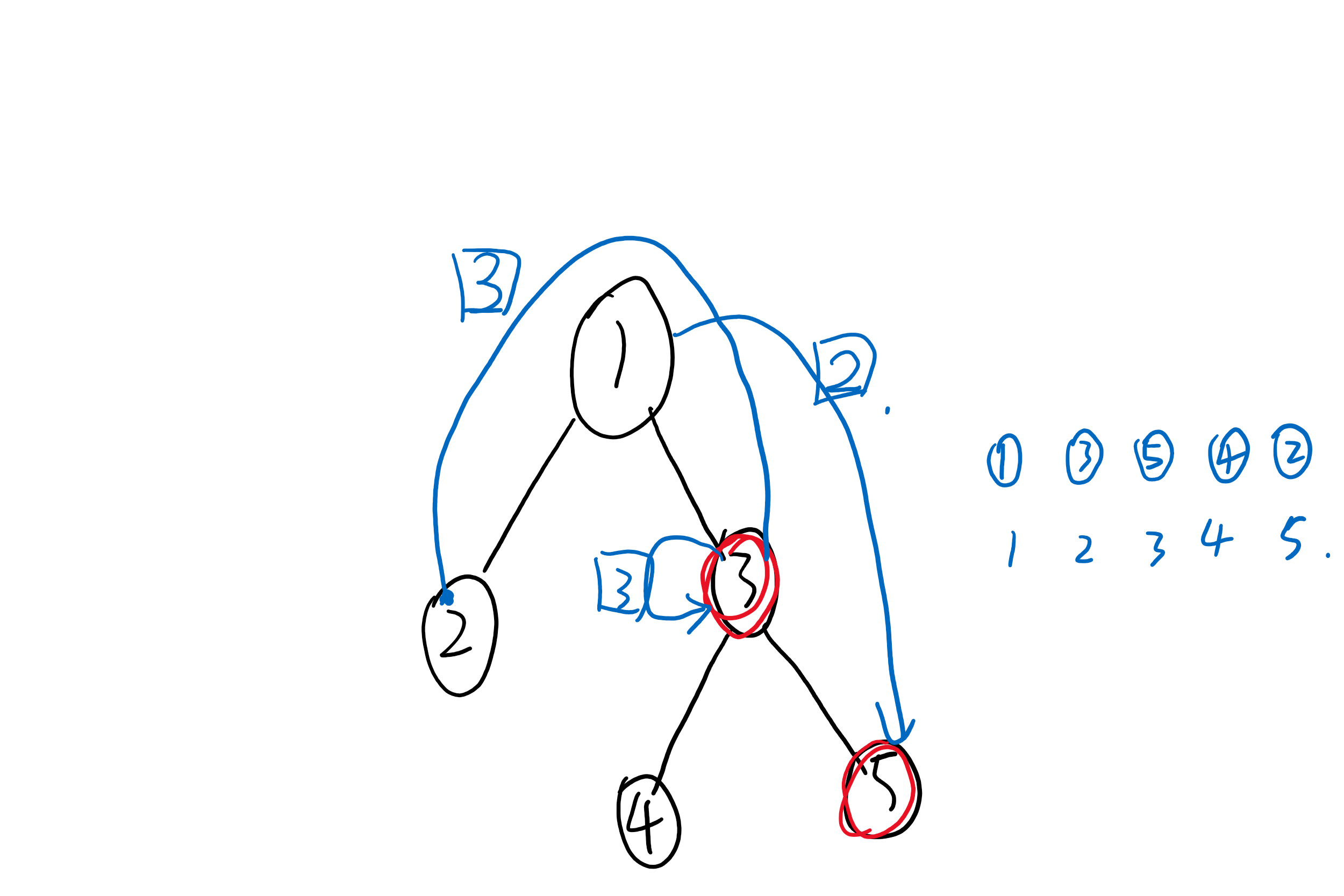
有这样三个操作,按照树链剖分的想法,还是希望 不在一条链上,处理这个链,到一个链上,整体处理(1,3,5一条链 2自己一条链 4自己一条链)。
第一个操作2到3,发现不是一条链,那么我们查询链头谁深度深,发现2深,处理2这条链,2跳到链头的父亲,也就是1,此时1 3在一条链上,处理1~3,后面两个也一样,我们找到点在序列里的位置,也就是\(id[x]\),能直接处理一条链是因为链上的点一定在序列里连续,而连续是因为我们优先走一条链上的。那么样例的操作就变成了对于区间某些不同部分的加。

三种颜色代表三次不同的操作,从图中很容易看出每个点的答案,4没有所以输出0
又因为题目要求,如果多种赈灾粮数量一样~请输出最少的,所以1的答案对2 3取min,就得到了2.
那么我们怎么让计算机实现我们的操作,又要记录什么呢?首先我们需要进行树链剖分,得到重儿子,一遍dfs就可以了,再一遍dfs得到链头,详情可见树剖模板部分[咳咳,非常不要脸的分享本蒟蒻写的
然后还要注意记录什么,链头是必须的,父亲是必须的,深度是必须的,跳的时候需要用。需不需要记录自己在序列中的位置呢?当然需要,题目给出你2,3这两个点,你不知道你的\(id\),你怎么把树上操作转化到序列里进行区间操作啊。所以树剖是需要记录的(有时候写着写着就发现少记东西了)
那么树剖完之后呢?怎么把操作变成区间操作,记录每一个操作的左边点和右边点?按左端点排序,左端点相同按右端点排序,然后往后走,扫到一个左端点就将其对应的粮食编号,\(cnt[opt.编号]++\)?然后每一次暴力跑一遍所有粮食?只有严格大于才记录,因为等于的时候,编号小更优[题目规定],粮食最大有\(1e5\),这么做能过吗?[不会算时间复杂度的蒟蒻不负责任地说:我猜不行
那怎么做呢?[打了又删...觉得语言无法说清楚,上代码吧,代码+注释应该好理解一些
要用到差分,比如对序列[l,r]操作,我们在[l]就加上一个标记,意思是在这里进行+z的操作,[r+1]打一个标记,意思是进行-z的操作[z就是对这个区间,给的粮食编号,那么区间操作就变成两个点的操作
//这个函数是下一个函数里的用的,可以先看下一个
void addopt(int a,int z){//添加操作函数 a是树变成 序列 后,你需要操作的位置,Z就是题目中给出的粮食编号
op[++num]=(opt){hd[a],z};//类似前向星,hd[a]存a的最后加进来的操作 op[cnt]存cnt这个操作的上一个操作,和这一个操作的值val
hd[a]=num;
}
void change(int x,int y,int z){//将所有加进来的x y区间 z粮食 操作进行拆分[从树上拆到序列里
while(top[x]!=top[y]){//不是一个链
if(dep[top[x]]<dep[top[y]])swap(x,y);//深度小的跳 这个理解不了就去看树链剖分模板
addopt(id[top[x]],z);//添加一个操作,链头~这个点,链头+z,这个点往后一个位置-z +z其实是这个位置开始有z这种粮食 -z是这个位置就没有这种粮食了
addopt(id[x]+1,-z);//差分的第二步
x=fa[top[x]];//跳[树剖模板
}
if(dep[x]>dep[y])swap(x,y);//模板
addopt(id[x],z);//拆成两个操作,这里x深度小,因为一个链,所以x一定在序列的前方,操作位置应该是先x所在位置,应当为[ID[X],ID[Y]]
addopt(id[y]+1,-z);
}
操作就拆到每一个点上了,现在点上存着 这里开始有某种粮食 和 这里某种粮食没有了 这两种信息,接下来处理操作 先假设\(modify\)与\(build\)正确,一会再传这两个
build(1,1,N);//建一棵权值线段树,每一个点存pos和cnt,记录这个区间出现最多的粮食是pos粮食,而pos粮食一共出现了cnt次
//存的是权值,比如根节点1~K的pos和cnt,记录1~K种类的粮食,我最多的是pos,出现了cnt次 比如说某一个叶子节点l到l,记录l这种粮食,我出现了cnt次
for(int i=1;i<=n;i++){//扫序列
for(int p=hd[i];p;p=op[p].pre){//类似前向星的扫操作
int v=op[p].val;//每一个操作的值
if(v>0){//如果是正的,说明从这里开始,我有v这种粮食了
modify(1,1,N,v,1);//1号结点,区间是1~N[粮食最多种类],v这种粮食,多一个
}
else{
modify(1,1,N,-v,-1);//否则是从这里v这种粮食少一份,也就是某一个树上操作变为序列操作后,正好没有包含到此结点
}
}
ans[reid[i]]=t[1].cnt?t[1].pos:0;//1号结点存目前有的[没有的在上面被减掉了]所有种类的粮食,如果cnt为0,说明1~N的粮食里,最多的出现了0次,那你就取0就完事了
//否则呢,我出现最多的就是pos粮食
}
void pushup(int x){
if(t[2*x].cnt>=t[2*x+1].cnt){//如果左儿子中目前最多的粮食次数>右儿子,那么我每次都选最多的,如果数量一样选编号最小的,所以如果相等,左儿子编号是l~mid一定比右儿子优
t[x].cnt=t[2*x].cnt;//我最多的就是左儿子中最多的
t[x].pos=t[2*x].pos;//我最多的pos就是左儿子的pos
}
else{//否则我取右儿子
t[x].cnt=t[2*x+1].cnt;
t[x].pos=t[2*x+1].pos;
}
}
void modify(int x,int l,int r,int pos,int d){
if(l==r){
t[x].cnt+=d;//找到pos位救济粮,将这个救济粮数量+d +1或者-1
return;
}
int mid=(l+r)>>1;
if(pos<=mid){//如果救济粮编号是l~mid
modify(x*2,l,mid,pos,d);
}
else if(mid+1<=pos){//如果不是
modify(x*2+1,mid+1,r,pos,d);
}
pushup(x);//把儿子的信息更新上来
}
//我试了一下,把build删掉,反正我们只需要更新叶子结点的pos,每次更新之后一定会更新到叶子节点(l==r才更新),所以pos都是来自于叶子节点,那么我们删掉build,直接在modify里,每次
//l==r时 加上一句t[x].pos=l;更新叶子结点,不知道这么做会不会出问题,但我提交之后过了,也可能是数据不强?
void build(int x,int l,int r){
if(l==r){
t[x].pos=l;//我这个位置,我出现最多的就是我自己[其实建树时没有任何粮食,没有出现多少这一说,但叶子节点初始化
return;
}
int mid=(l+r)>>1;
build(x*2,l,mid);//左右递归!
build(x*2+1,mid+1,r);
pushup(x);//合并儿子信息 其实不合并也可以,其实我只需要初始化叶子结点就可以了,不初始化叶子结点你的所有pos都是0 赋值也是0,pos就永远不会改变,操作也只是修改数量,不会修
//改pos的
}
完整代码:
一开始没有删除build中的pushup和build的版本,至于删其中的pushup。或者删掉build将叶子初始化改到modify里,提交貌似可以A?至于正不正确就不知道了[懒得对拍
op数组一定要开大一点!树操作转化成链操作会变多,可能会爆下标什么的[而且还会说TLE和WA?竟然不是RE
#include<bits/stdc++.h>
using namespace std;
const int N=1E5+86;
int n,m;
int h[N],cnt=0;
int fa[N],dep[N],son[N],si[N],id[N];
int top[N],tot=0,hd[N],num=0,reid[N];//转化为链后 每一个点记它最后一个操作编号
struct Tre{
int cnt,pos;//最大值是多少,是哪种救济粮
}t[N<<4];
struct opt{
int pre,val;
}op[N*20];//记操作的上一个操作的编号,记这个操作进行了什么改动
struct edg{
int to,nxt;
}e[N<<1];
void add(int x,int y){
e[++cnt]=(edg){y,h[x]};
h[x]=cnt;
}
void dfs(int x,int f){
fa[x]=f;dep[x]=dep[f]+1;si[x]=1;
for(int p=h[x];p;p=e[p].nxt){
int to=e[p].to;
if(to==f)continue;
dfs(to,x);
si[x]+=si[to];
if(si[to]>si[son[x]] || !son[x]){
son[x]=to;
}
}
}
void Dfs(int x,int topf){
top[x]=topf;
id[x]=++tot;
reid[tot]=x;
if(!son[x])return;
Dfs(son[x],topf);
for(int p=h[x];p;p=e[p].nxt){
int to=e[p].to;
if(to==son[x] || to==fa[x])continue;
Dfs(to,to);
}
}
void addopt(int a,int z){
op[++num]=(opt){hd[a],z};
hd[a]=num;
}
void change(int x,int y,int z){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
addopt(id[top[x]],z);
addopt(id[x]+1,-z);
//if(x==2)printf("fa[2]=%d\n",fa[x]);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
addopt(id[x],z);
addopt(id[y]+1,-z);
}
void pushup(int x){
//printf("ls.cnt pos=%d %d rs.cnt pos=%d %d\n",t[2*x].cnt,t[2*x+1].pos,t[2*x].cnt,t[2*x+1].pos);
if(t[2*x].cnt>=t[2*x+1].cnt){
t[x].cnt=t[2*x].cnt;
t[x].pos=t[2*x].pos;
}
else{
t[x].cnt=t[2*x+1].cnt;
t[x].pos=t[2*x+1].pos;
}
}
void modify(int x,int l,int r,int pos,int d){
if(l==r){
t[x].cnt+=d;//找到pos位救济粮,将这个救济粮数量+d
return;
}
int mid=(l+r)>>1;
if(pos<=mid){
modify(x*2,l,mid,pos,d);
}
else if(mid+1<=pos){
modify(x*2+1,mid+1,r,pos,d);
}
//printf("l=%d r=%d pos=%d d=%d\n",l,r,pos,d);
pushup(x);
}
void build(int x,int l,int r){
if(l==r){
t[x].pos=l;
//printf("l=%d,pos=%d\n",l,t[x].pos);
return;
}
int mid=(l+r)>>1;
build(x*2,l,mid);
build(x*2+1,mid+1,r);
pushup(x);
}
int ans[N];
int main(){
scanf("%d%d",&n,&m);
for(int a,b,i=1;i<n;i++){
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
dfs(1,0);
Dfs(1,1);
for(int a,b,z,i=1;i<=m;i++){
scanf("%d%d%d",&a,&b,&z);
change(a,b,z);
}
build(1,1,N);
for(int i=1;i<=n;i++){
for(int p=hd[i];p;p=op[p].pre){
int v=op[p].val;
//printf("i=%d v=%d\n",i,v);
if(v>0){
modify(1,1,N,v,1);
}
else{
modify(1,1,N,-v,-1);
}
}
//printf("t[1]cnt =%d pos=%d\n",t[1].cnt,t[1].pos);
ans[reid[i]]=t[1].cnt?t[1].pos:0;
}
for(int i=1;i<=n;i++){
printf("%d\n",ans[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号