圆的异或并 扫描线2

上次的扫描线[包括窗口的星星]都是使用线段树实现的
但扫描线可能更多是一种思想，实际上并不存在那么一条线，只是你按照某种顺序排序，让处理二维问题变得简单。
一道新题:圆的异或并

题目大意:给定n，然后给定n个圆[圆心坐标+半径]，异或就是那么个异或，最后输出面积除以PI。

跟矩形面积并的区别就是一个是矩形一个是圆形，咳咳，其实主要是一个是重叠部分就算，而这道题是重叠奇数次才算，重叠如果是偶数次就不算了。

题目限制:圆无交点->不交不切->要么相离要么包含。

数据范围:|x|,|y|,<=10^8，r>0,N<=200000

那么这道题要怎么考虑呢，我们发现要么相离要么包含，所以我们如果将圆的包含看作是一个父亲与孩子的关系，就会出现很多树。

比如一个这样的图，右边是它的树。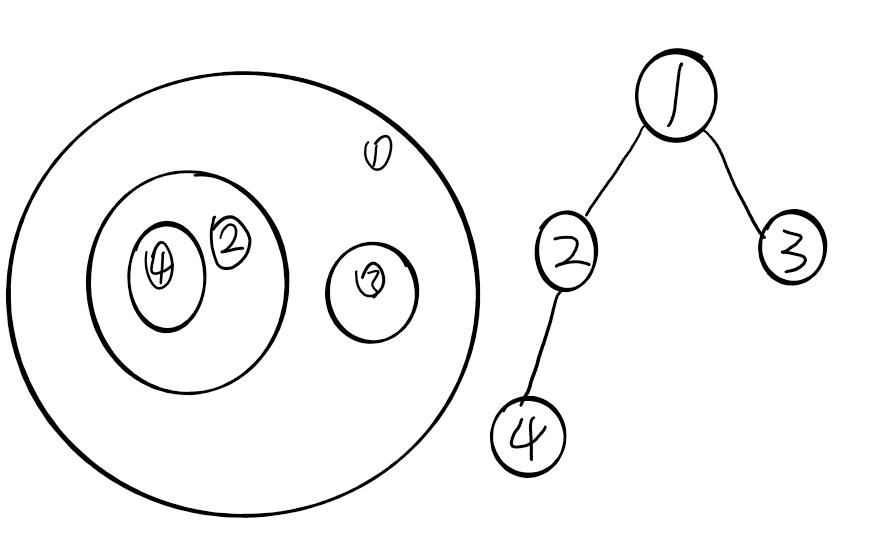
那么我们注意到，如果一个结点，也就是一个圆，它的深度如果是一个奇数[把根节点，也就是最外面不被包含的圆深度设为0]，这里的面积就应该减掉，偶数的要加上它的面积。

问题转化成了怎么算出每个圆的深度，因为面积除以PI很容易得到，可以\(O(1)\)算，所以只需要知道面积的正负即可

如果我们按照x从小到大扫过去，我们发现一个圆如果被其他圆包含，包含它的圆一定会先被扫到，当加进来一个圆的左端点时，画一画图，发现如果扫描线上，这个点无法同时找到比它高的和比它低的，说明这个圆不会被包含。
分类讨论得到这么个玩意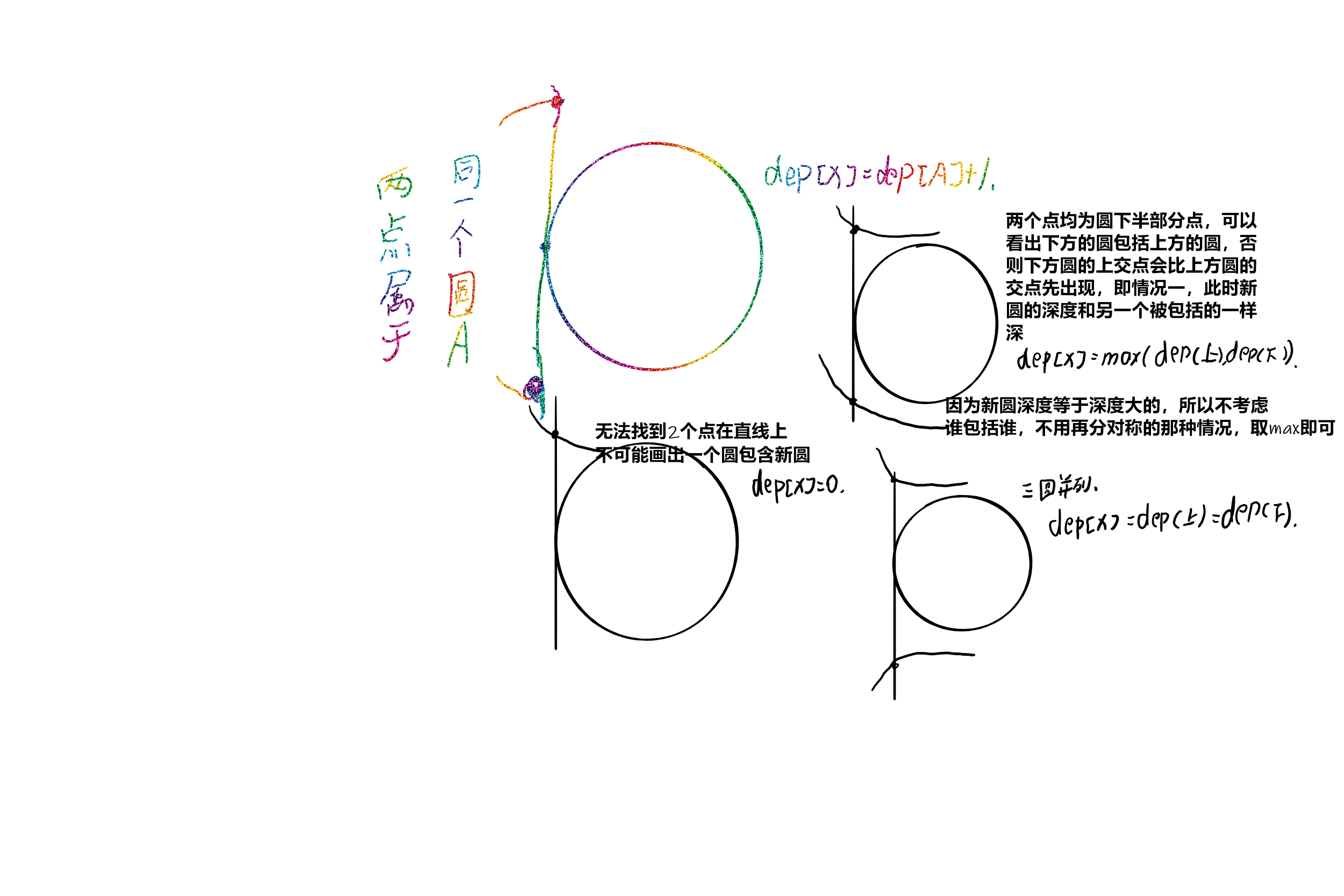
于是这道题就可以做了
代码[后面有详细一点的讲

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+8;
int n;
int in;
int dep[N],x[N],y[N],r[N];
double Getins(int id,int ud){
    double ins=sqrt(1.00*r[id]*r[id]-(1.00*in-x[id])*(1.00*in-x[id]));
    return ud==1?y[id]+ins:y[id]-ins;
}
struct event{
    int x,f,num;
    bool operator < (const event &t)const{
        return x<t.x;
    }
}eve[2*N];
struct point{
    int id,ud;
    bool operator < (const point &t)const{
        if(id==t.id)return ud>t.ud;
        return Getins(id,ud)>Getins(t.id,t.ud);
    }
};
set <point> S;
set <point> ::iterator it1,it2;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d%d",&x[i],&y[i],&r[i]);
        eve[i]=(event){x[i]-r[i],1,i};
        eve[n+i]=(event){x[i]+r[i],-1,i};
    }
    sort(eve+1,eve+2*n+1);//将这些事件(扫描点)进行排序
    for(int i=1;i<=2*n;i++){//处理事件
        in=eve[i].x;
        if(eve[i].f==1){
            it1=it2=S.insert((point){eve[i].num,1}).first;
            ++it2;
            if(it1==S.begin() || it2==S.end()){
                dep[eve[i].num]=0;
            }
            else{
                --it1;
                if(it1->id == it2->id)dep[eve[i].num]=dep[it1->id]+1;
                else if(dep[it1->id]==dep[it2->id])dep[eve[i].num]=dep[it1->id];
                else dep[eve[i].num]=max(dep[it1->id],dep[it2->id]);
            }
            S.insert((point){eve[i].num,0});
        }
        else{
            S.erase((point){eve[i].num,1});
            S.erase((point){eve[i].num,0});
        }
    }
    long long ans=0;
    for(int i=1;i<=n;i++){//最后一位是1就是- 是0就是+
        if(dep[i]&1)ans-=1ll*r[i]*r[i];
        else ans+=1ll*r[i]*r[i];
    }
    printf("%lld\n",ans);
    return 0;
}

for(int i=1;i<=n;i++){
        scanf("%d%d%d",&x[i],&y[i],&r[i]);//读入圆心坐标和半径
        eve[i]=(event){x[i]-r[i],1,i};//左端点，是加入操作，这个操作属于圆i
        eve[n+i]=(event){x[i]+r[i],-1,i};//右端点，删除操作，操作属于圆i
    }
    sort(eve+1,eve+2*n+1);//将这些事件(扫描点)按端点进行排序[自行在结构体内重载运算符

double Getins(int id,int ud){//联立求交点 在洛谷上int类型返回值竟然A了 id是记录哪一个圆 ud是up还是down[上下交点
    double ins=sqrt(1.00*r[id]*r[id]-(1.00*index-x[id])*(1.00*index-x[id]));//解一下方程
    return ud==1?y[id]+ins:y[id]-ins;返回交点
}
struct point{
    int id,ud;//属于哪个圆 上还是下交点
    bool operator < (const point &t)const{
        if(id==t.id)return ud>t.ud;//同一个圆上交点比下交点高[即使你们实际都刚加入是相等的
        return Getins(id,ud)>Getins(t.id,t.ud);//返回到底谁高
    }
};

set <point> S;//set是不可重集合，会自行排序，所以在这里面找前驱后继还是比较快的 <point>表示存储的point结构体，S是名字，就像int x
set <point> ::iterator it1,it2;//迭代器it1和it2，要用迭代器来返回set内的值
for(int i=1;i<=2*n;i++){//处理事件
        in=eve[i].x;//index 基准 意思是当前扫描线的x值 注:index貌似用了会CE，就像万能头用y1(还是y2)一样，所以变量名要小心
        if(eve[i].f==1){//如果是新加点操作
            it1=it2=S.insert((point){eve[i].num,1}).first;//set插入会返回一个pair first是位置，用first可以快速得到这个值插入到了第几位，second是个bool判断是否插入成功
            ++it2;//迭代器2往后找比它低的点[后继
            if(it1==S.begin() || it2==S.end()){//如果自己本身是第一个点 或者后继无人 则是上文提到的无法找全前驱后继，dep为0
                dep[eve[i].num]=0;//是这个圆的dep为0，而不是第i个操作
            }
            else{
                --it1;//否则找前驱
                if(it1->id == it2->id)dep[eve[i].num]=dep[it1->id]+1;//it1->id 就是迭代器所在位置point的id[因为存储的是point结构体]就类似于结构体的 x.id
                //同一个圆 深度为大圆+1
                else if(dep[it1->id]==dep[it2->id])dep[eve[i].num]=dep[it1->id];//若深度一样，随便取
                else dep[eve[i].num]=max(dep[it1->id],dep[it2->id]);//否则取深的 兴许和上面的合并也没事？
            }
            S.insert((point){eve[i].num,0});//再把下方的点也插进去 为了以后的圆查找做准备
        }
        else{//不是插入操作
            S.erase((point){eve[i].num,1});//暴力删除上面这个点 erase是删除
            S.erase((point){eve[i].num,0});//暴力删除下面的点
        }
    }

for(int i=1;i<=n;i++){//最后一位是1就是- 是0就是+
        if(dep[i]&1)ans-=1ll*r[i]*r[i];
        else ans+=1ll*r[i]*r[i];
    }

到这里这道题基本上就结束了，配个结束语。

一切过往，皆为序章。