扫描线

扫描线，顾名思义，就是一条线，从某一个方向扫描过去的算法。
扫描线的一道例题就是矩形面积并
题目的意思是给出多个矩形[左下角和右上角坐标]，那么求最后在平面上覆盖的面积。
题目链接

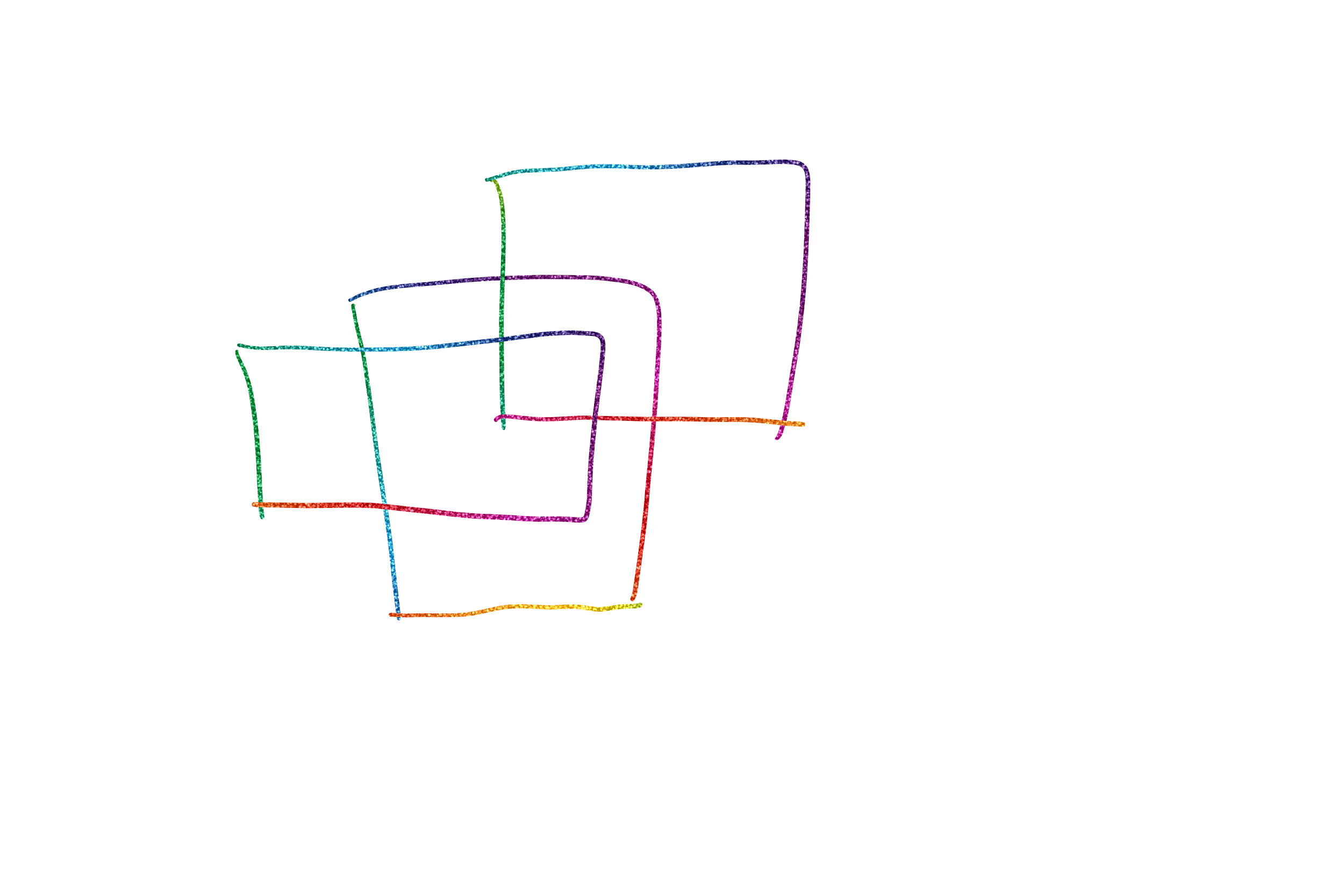
暴力就全打一遍标记，然后扫一遍，肯定是过不去。
接下来就轮到扫描线出场了，我们拿一条平行于y轴，或者平行于x轴的直线，从0一直往后扫。
假设用平行于x轴的，对于每一个y，我们发现只有扫到矩形的边，才会使这个y值的贡献改变，比如说上面那张图。

我们先扫到最下面的边，那这条线段所覆盖区间打上标记。我们发现，我们不需要一点点扫，因为直到下一条边加进来，我们这条线上被覆盖的长度是不变的。所以我们完全可以一条边一条边扫。
碰到矩形的下边界，那么某一段区域就打上标记，碰到上边界，就撤销一次标记，表示这里不再被这个矩形覆盖。
那么这条线给的贡献就是\((下一条边y值-这一条边y值)\times这条线加入后被覆盖的面积\)

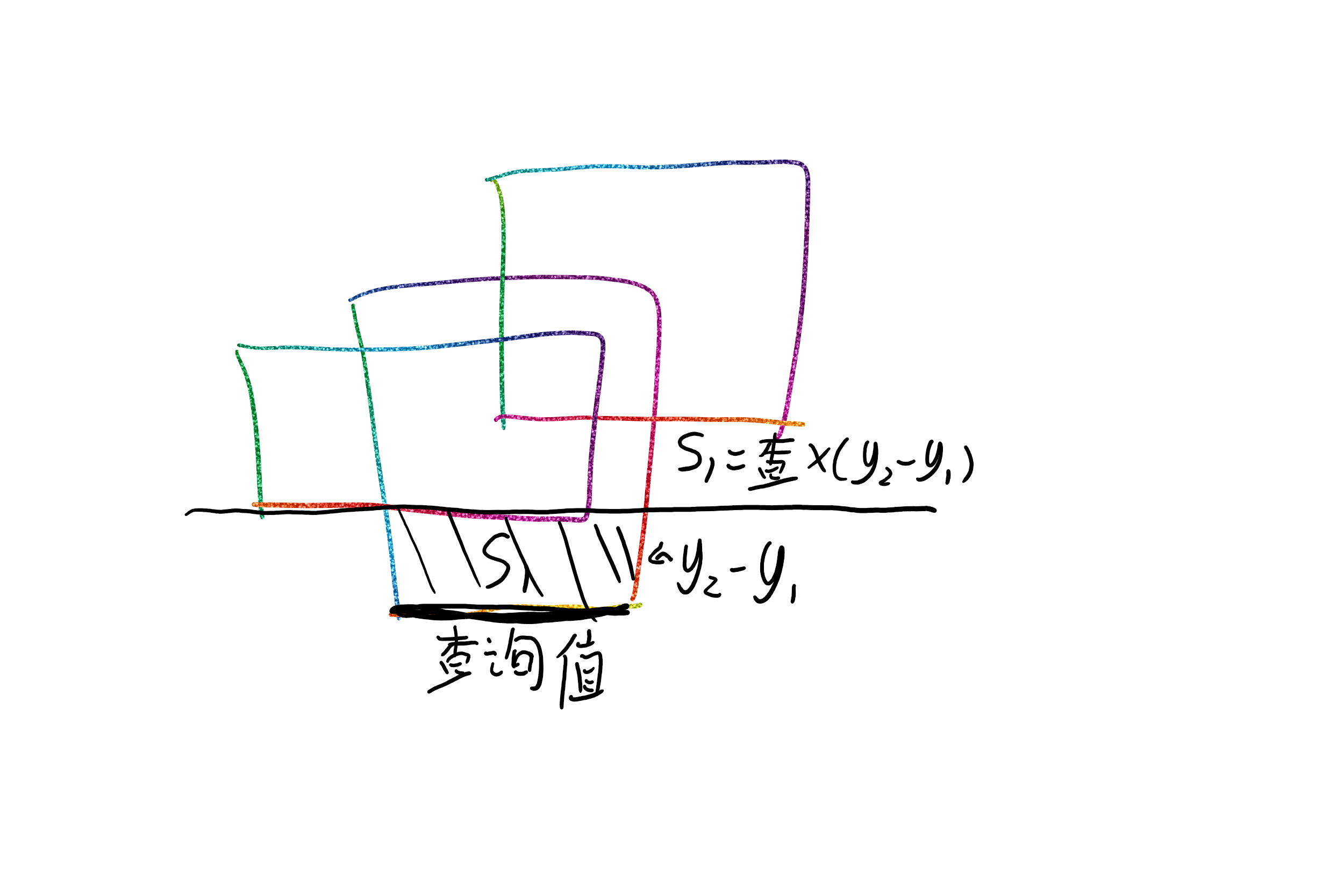
于是接下来就可以将矩形覆盖面积重新分拆，变成这样：

那么怎么用计算机实现这个操作呢？关于扫描，其实我们不需要真的扫，我们注意到扫描就是一条条线从下到上处理，于是我们就可以将线段[结构体]存下来，按照高度排序，还需要存覆盖范围和线段类型[+还是-]
这样我们就实现了扫描的过程，那么高度差值\(y_2-y_1\)的处理好说，从线段里面拿出来高度减一下就行，如何快速的查询此时扫描线上被覆盖的长度呢，同时如何快速的进行我们上面所说的操作呢？
如果每一次都暴力的遍历一次，最坏的复杂度是2*n条边(一个矩形扫两个边)，每次跑最长长度1e9，肯定是过不去。(蒟蒻不会算时间复杂度就不写了，大概是O(nlen)吧
我们发现，上面的操作其实是，区间+1，区间-1，区间求和，区间修改区间求和，我们当然可以用线段树维护。
因为我们是平行于x轴，所以线段树要建在x轴上。
于是我们建一个x轴上的线段树，1e9，线段树再开四倍空间，MLE。
但其实没有必要，n只有1e5，开1e9的范围，中间空的点太多太多，我们没有必要开如此巨大，我们可以进行离散化。详细的可以见代码[感觉有点解释不清]
然后就是线段树存什么，首先t[x]存一个标记[是否被覆盖]，再存一个实际长度就可以了[我习惯把左右端点作为参数传进去]，然后就是这里一个点其实对应的是一段区间，比如说如果你查询l到r，查询了l到mid加上mid+1到r，你会忽略掉mid~mid+1之间是存在一段距离的，所以这里我们线段树的一个点，比如t[x]，假设它的左右端点是l和r，它就表示\(X[l]~X[r+1]\)这样一个区间，也就是一个点对应的是x轴上的一段。
读入操作

scanf("%d",&n);
    for(int i=1;i<=n;i++){
        LL xa,ya,xb,yb;
        scanf("%lld%lld%lld%lld",&xa,&ya,&xb,&yb);
        x[i]=xa,y[i]=ya,x[n+i]=xb,y[i+n]=yb;//矩形的左下右上点
        opt[i].l=x[i];opt[i].r=x[n+i];opt[i].pos=y[i];opt[i].ty=1;//线段操作区间就是矩形两端的x，高度为底边的y，操作是+1
        opt[i+n].l=x[i];opt[i+n].r=x[n+i];opt[i+n].pos=y[i+n];opt[i+n].ty=-1;//区间相同，高度为顶边的y，操作是-1
    }

然后opt数组按y排序，至于同y先+还是-...好像没有区别，就不用管了。x数组排序并去重。我这里并没有把x数组转化，因为我存进线段的就是真实x，到时候比较也不用比较离散化后的值，直接比就可以。然后按顺序加边。

for(int i=1;i<2*n;i++){//不到2*n是因为最后一条边没有必要处理，反正上面没有了
        update(1,1,len-1,opt[i].l,opt[i].r,opt[i].ty);//加边,我这里传参 (x,x的l，x的r，查询的实际左端点也就是x左，x右，操作是什么）
        ans+=(opt[i+1].pos-opt[i].pos)*(t[1].sum);//更新答案
    }

关于pushdown[下放标记]，有大佬说

这题如果一个结点不再被覆盖了要用子节点被覆盖的值更新它，如果标记被下传了，整棵子树都被覆盖一次，不再覆盖时要遍历整棵子树重新获取信息，所以这题只能用记录本区间覆盖次数的方式

void update(int now,int l,int r,int L,int R,int d){
    if(R<=x[l] || x[r+1]<=L)return;//如果实际增加区间在此结点左或者右，用实际值比，可以取等是因为本点代表l~(r+1)的区间，而覆盖到x[l]并不会覆盖上面的区间，故相等也return
    if(L<=x[l] && x[r+1]<=R){
        t[now].tag+=d;//整个被覆盖就打标记，至于是+1还是-1不清楚
        if(t[now].tag)t[now].sum=x[r+1]-x[l];//如果更改后仍是被覆盖状态，被覆盖总长[sum]=x[r+1]-x[l],为什么是r+1还是那个道理，点映射到区间上，代表的是l~(r+1)
        if(!t[now].tag)t[now].sum=t[now*2].sum+t[now*2+1].sum;
        //如果更改后就不被覆盖了，那么总长度就是儿子被覆盖长度和。
        return;
    }
    //不要下传标记，血的教训，因为你其实一个区间如果被覆盖满了，就不需要往子树传递，因为未来如果你tag变0，你想知道之前在你完全被覆盖之前，孩子结点啥样，晚了，你已经下放了
    //下放之后儿子变为完全被覆盖，确实是这样的，但是它们上一次的长度你就不知道了，sum被赋满，那么这条边删除后，儿子实际sum不再是总长度，而你下放之后变为总长度，就会导致错误
    //pushdown(now,l,r);//标记下传
    int mid=(l+r)>>1;
    update(now*2,l,mid,L,R,d);//左区间
    //puts("---");
    update(now*2+1,mid+1,r,L,R,d);//右区间
    if(t[now].tag)t[now].sum=x[r+1]-x[l];
    if(!t[now].tag)t[now].sum=t[now*2].sum+t[now*2+1].sum;//标记留着更新自己就可以，每次你都会把所有标记上传回去，直到传到1号结点，所以下传会影响儿子对自己的上传
}

回头打算记录一下窗口的星星，其实不会，挖坑，未来也许会填。