(联考)noip68
T1
考场想法:瞎几把搜,给自己搜死了。
至今不知道为啥错了,反正数据都是hack我的数据。
正解:
简单的找规律题。
先考虑只找两条路径的情况,那么只需要存在一个位置 \((i,j)\) 满足 \(a_{i+1,j}=a_{i,j+1}\) 即可。不妨称这样的位置 \(i,j\) 为 \(good\) 的位置。
考虑扩展到找三条路径的情况。
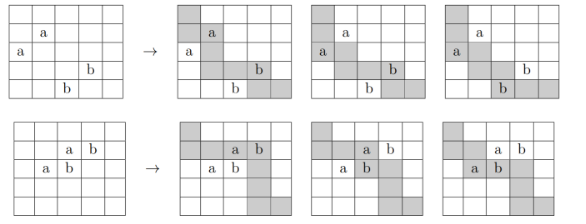
图是嫖的题解的。
那么实际上只有图中的两种情况:
-
有两个 \(good\) 的位置 \((i_{1},j_{1}),(i_{2},j_{2})\) ,满足 \(i_{1}<i_{2}\) 且 \(j_{1}<j_{2}\)
-
存在两个相邻的 \(good\) 位置。
用个前缀和维护即可。
T2
考场想法:只会 \(k=1\) 的点。
30pts:写个背包即可, \(dp_{i,j}\) 表示前 \(i\) 个,长度为 \(j\) 的最大愉♂悦值。
40pts:加上 \(k=1\) 的点。
正解:

T3
考场想法:没写,不会。
话说,这是个显然的网络流匹配都没看出来qwq。
20pts:网络流即可。源点向出题人连边,容量为对应的出题数量,验题人向汇点连边,容量为对应的验题数量,出题人向所有验题人连一条容量为1的边,每回修改重新建图,跑遍最大流,看是否等于当前总出题数量即可。
正解:

式子可以自己举个例子模一下。
线段树实际上维护的是前缀和。
-
对于1/2操作,为了方便,这里又给 \(a\) 从小到大排序了一遍,如果 \(a_{i}\) 在查找数组里的位置为 \(p\) ,那么对应在从大到小的数组里的位置即为 \(n-p+1\) 。 找出 \(a_{i}\) 最后一次/第一次出现的位置++/--,不会影响大小关系,根据式子可知,如果修改了 \(a_{i}\) ,那么影响的是 \(a_{i}\) 在递减数组里的位置 \(n-p+1\) 一直到 \(n\) ,对应的-1/+1 即可。
-
对于3操作, \(b_{i}\)+1的话, \(c_{b_{i}}\) 没有发生变化, \(c_{b_{i}+1}\) 倒是多了个1,式子是求和,线段树维护的是前缀和,那么应该修改的则是 \([b_{i}+1,n]\) (修改前的 \(b_{i}\) ) 这段区间,4操作同理, \(b_{i}-1\) , \(c-{b_{i}-1}\) 不变, \(c_{b_{i}}\) 减少了1,那么修改的就应该是 \([b_{i},n]\) (修改前) 这段区间。对应+1/-1即可。
Code
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<climits>
#include<algorithm>
#define MAX 250003
#define re register
#define INF INT_MAX
using std::queue;
using std::sort;
using std::lower_bound;
using std::upper_bound;
namespace some
{
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
bool w=0; s=0; char ch=getchar();
while(!isdigit(ch)){ w|=ch=='-'; ch=getchar(); }
while(isdigit(ch)){ s=(s<<1)+(s<<3)+(ch^48); ch=getchar(); }
return s=w?-s:s,*this;
}
}cin;
int sum[MAX];
int rec,res;
int n,m,q,s,t;
int a[MAX],b[MAX],c[MAX],sd[MAX];
auto max = [](int a,int b) { return a>b?a:b; };
auto min = [](int a,int b) { return a<b?a:b; };
}using namespace some;
namespace Graph
{
struct graph
{
int next;
int to;
int w;
}edge[MAX<<1];
int cnt=1,head[MAX][2];
auto add = [](int u,int v,int w)
{
edge[++cnt] = (graph){head[u][0],v,w},head[u][0] = cnt;
edge[++cnt] = (graph){head[v][0],u,0},head[v][0] = cnt;
};
int dis[MAX];
auto bfs = []() -> bool
{
queue<int>q; q.push(s);
for(re int i=1; i<=t; i++)
{ dis[i] = 0; }
head[s][1] = head[s][0];
while(!q.empty())
{
int u = q.front(); q.pop();
for(re int i=head[u][0],v; i; i=edge[i].next)
{
v = edge[i].to;
if(edge[i].w&&!dis[v])
{
q.push(v);
dis[v] = dis[u]+1;
head[v][1] = head[v][0];
if(v==t)
{ return 1; }
}
}
}
return 0;
};
int dinic(int u,int flow)
{
if(u==t)
{ return flow; }
int rest = flow;
for(re int i=head[u][1],v; i&&rest; i=edge[i].next)
{
v = edge[i].to;
if(edge[i].w&&dis[v]==dis[u]+1)
{
int k = dinic(v,min(edge[i].w,rest));
if(!k)
{ dis[v] = 0; }
rest -= k;
edge[i].w -= k;
edge[i^1].w += k;
}
head[u][1] = i;
}
return flow-rest;
}
}using namespace Graph;
namespace simple
{
auto solve = []() -> void
{
for(re int i=1; i<=n; i++)
{ rec += a[i]; }
for(re int i=1,opt,id; i<=q; i++)
{
res = 0;
cin >> opt >> id;
if(opt==1) { a[id]++; rec++; }
if(opt==2) { a[id]--; rec--; }
if(opt==3) { b[id]++; }
if(opt==4) { b[id]--; }
cnt = 1;
memset(head,0,sizeof(head));
for(re int j=1; j<=n; j++)
{ add(s,j,a[j]); }
for(re int j=1; j<=m; j++)
{ add(j+n,t,b[j]); }
for(re int j=1; j<=n; j++)
{
for(re int k=1; k<=m; k++)
{ add(j,k+n,1); }
}
while(bfs())
{ res += dinic(s,INF); }
printf("%d\n",res==rec);
}
};
};
namespace Segment_TREE
{
struct Segment_Tree
{
struct TREE
{ int val,lazy; }st[MAX<<2];
#define ls(p) p<<1
#define rs(p) p<<1|1
#define mid (l+r>>1)
void Push_up(int p)
{ st[p].val = min(st[ls(p)].val,st[rs(p)].val); }
void Push_down(int p)
{
if(st[p].lazy)
{
st[ls(p)].val += st[p].lazy;
st[rs(p)].val += st[p].lazy;
st[ls(p)].lazy += st[p].lazy;
st[rs(p)].lazy += st[p].lazy;
st[p].lazy = 0;
}
}
void build(int p,int l,int r)
{
if(l==r)
{ st[p].val = sum[l]; return ; }
build(ls(p),l,mid),build(rs(p),mid+1,r);
Push_up(p);
}
void modify(int p,int l,int r,int lp,int rp,int w)
{
if(l>r)
{ return ; }
if(lp<=l&&r<=rp)
{ st[p].val += w,st[p].lazy += w; return ; }
Push_down(p);
if(lp<=mid)
{ modify(ls(p),l,mid,lp,rp,w); }
if(rp>mid)
{ modify(rs(p),mid+1,r,lp,rp,w); }
Push_up(p);
}
}Tree;
}using namespace Segment_TREE;
namespace Made_In_Heaven
{
auto solve = [](int top = 0) -> void
{
sort(a+1,a+1+n,[](const int &x,const int &y){ return x>y; });
for(re int i=1; i<=m; i++)
{ c[b[i]]++,top = max(top,b[i]); }
for(re int i=top-1; i; i--)
{ c[i] += c[i+1]; }
//for(re int i=1; i<=n; i++) { printf("c[%d]=%d\n",i,c[i]); }
for(re int i=1; i<=n; i++)
{ sum[i] = sum[i-1]+c[i]-a[i]; }
sort(a+1,a+1+n); Tree.build(1,1,n);
for(re int i=1,opt,id,p; i<=q; i++)
{
cin >> opt >> id;
if(opt==1)
{
p = upper_bound(a+1,a+1+n,sd[id])-a-1;
sd[id]++,a[p]++,p = n-p+1;
Tree.modify(1,1,n,p,n,-1);
}
if(opt==2)
{
p = lower_bound(a+1,a+1+n,sd[id])-a;
sd[id]--,a[p]--,p = n-p+1;
Tree.modify(1,1,n,p,n,1);
}
if(opt==3)
{ b[id]++; Tree.modify(1,1,n,b[id],n,1); }
if(opt==4)
{ Tree.modify(1,1,n,b[id],n,-1); b[id]--; }
printf("%d\n",Tree.st[1].val>=0);
}
};
};
namespace OMA
{
auto main = []() -> signed
{
//freopen("node.in","r",stdin); freopen("my.out","w",stdout);
freopen("problem.in","r",stdin); freopen("problem.out","w",stdout);
cin >> n >> m; s = 0,t = n+m+1;
for(re int i=1; i<=n; i++)
{ cin >> a[i]; sd[i] = a[i]; }
for(re int i=1; i<=m; i++)
{ cin >> b[i]; }
cin >> q;
//simple::solve();
Made_In_Heaven::solve();
return 0;
};
}
signed main()
{ return OMA::main(); }
考场都没有想到网络流,还是菜了,虽说是联赛模拟,但也不一定只考联赛知识点啊,思维要发散一些,实在啥也想不到了,就把自己学过的都想一遍,看有没有能用的上的,如果还没有,那估计就是dp或者什么神仙题了。
T4
考场想法:直接搜,暴力check,其他真的什么都想不到。
10pts。
正解:
要用LCT,高级东西,不会,咕了。

