noip37
为何我对T3情有独钟
T1
不难发现,题目要求的就是 \(ax+by=c\) ,已知 \(a,b,c\) ,求 \(\min\{|a|+|b|\}\) ,那就用扩欧求一组特解,再分情况讨论即可。
Code
#include<cstdio>
#define MAX 100010
#define re register
#define int long long
namespace OMA
{
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
inline int exgcd(int a,int b,int &x,int &y)
{
if(!b)
{ x = 1,y = 0; return a; }
int d = exgcd(b,a%b,x,y);
int z = x; x = y; y = z-y*(a/b);
return d;
}
inline int min(int a,int b)
{ return a<b?a:b; }
inline int abs(int a)
{ return a>=0?a:-a; }
int n,a,b,x[MAX],ans;
signed main()
{
cin >> n >> a >> b;
if(a>b)
{ int t=a; a=b; b=t; }
int xi,yi;
int gcd = exgcd(a,b,xi,yi);
a /= gcd,b/= gcd;
for(re int i=1; i<=n; i++)
{
cin >> x[i];
if(x[i]%gcd)
{ printf("-1\n"); return 0; }
}
for(re int i=1,x1,y1,k; i<=n; i++)
{
x1 = xi*x[i]/gcd,y1 = yi*x[i]/gcd,k = abs(x1/b);
if(x1>=0&&y1<=0)
{ ans += min(abs(x1-k*b)+abs(y1+k*a),abs(x1-(k+1)*b)+abs(y1+(k+1)*a)); }
else if(x1<=0&&y1>=0)
{ ans += min(abs(x1+k*b)+abs(y1-k*a),abs(x1+(k+1)*b)+abs(y1-(k+1)*a)); }
}
printf("%lld\n",ans);
return 0;
}
}
signed main()
{ return OMA::main(); }
T2
考场上一眼看上去像队长快跑,然而带权。
但其实如果那道题真的明白了,这道也不算难。
然而我...
首先写出基础dp,设 \(dp_{i,j}\) 表示当前选到了第 \(i\) 个数对,其中,所选的数对中最大的 \(a\) 为 \(j\),则可以列出转移方程:
- 选 \(i\) 后,最大值不是 \(a_{i}\) ,则,
\[dp_{i,j} = \max\{dp_{i-1,j}\}+w_{i}\;,j\in[a_{i},b_{i}]
\]
- 选 \(i\) 后,最大值为 \(a_{i}\) ,则,
\[dp_{i,a_{i}} = \max\{dp_{i-1,j}\}+w_{i}\;,j\in[1,\min(a_{i},b_{i})]
\]
- 不选,直接由上层转移,则,
\[dp_{i,j}=\max\{dp_{i-1,j}\}\;,j\in[1,max]
\]
列出来后,直接转移,时空双爆,60pts。
观察式子,发现可以用线段树来维护,1操作对应区间修改,2操作对应单点修改,3操作不用管,会直接覆盖。
复杂度 \(O(n\log n)\)
附基础dp
Code
#include<cstdio>
#include<algorithm>
#define MAX 100010
#define re register
#define int long long
using std::sort;
using std::unique;
using std::lower_bound;
namespace OMA
{
int n,cnt;
int tmp[MAX<<1];
int dp[6010][6010];
struct node
{
int a,b,w;
inline friend bool operator <(const node &a,const node &b)
{ return a.a+a.b<b.a+b.b; }
}p[MAX];
inline int max(int a,int b)
{ return a>b?a:b; }
inline int min(int a,int b)
{ return a<b?a:b; }
struct Segment_Tree
{
struct TREE
{
int l,r;
int val;
int lazy;
}st[MAX<<3];
inline int ls(int p)
{ return p<<1; }
inline int rs(int p)
{ return p<<1|1; }
inline void Push_up(int p)
{ st[p].val = max(st[ls(p)].val,st[rs(p)].val); }
inline void Push_down(int p)
{
if(st[p].lazy)
{
st[ls(p)].val += st[p].lazy;
st[ls(p)].lazy += st[p].lazy;
st[rs(p)].val += st[p].lazy;
st[rs(p)].lazy += st[p].lazy;
st[p].lazy = 0;
}
}
inline void build(int p,int l,int r)
{
st[p].l = l,st[p].r = r;
if(l==r)
{ return ; }
int mid = (l+r)>>1;
build(ls(p),l,mid),build(rs(p),mid+1,r);
}
inline void update1(int p,int l,int r,int val)
{
if(l>r)
{ return ; }
if(l<=st[p].l&&st[p].r<=r)
{ st[p].val += val,st[p].lazy += val; return ; }
Push_down(p);
int mid = (st[p].l+st[p].r)>>1;
if(l<=mid)
{ update1(ls(p),l,r,val); }
if(r>mid)
{ update1(rs(p),l,r,val); }
Push_up(p);
}
inline void update2(int p,int pos,int val)
{
if(st[p].l==st[p].r)
{ st[p].val = max(st[p].val,val); return ; }
Push_down(p);
int mid = (st[p].l+st[p].r)>>1;
if(pos<=mid)
{ update2(ls(p),pos,val); }
else
{ update2(rs(p),pos,val); }
Push_up(p);
}
inline int query(int p,int l,int r)
{
if(l<=st[p].l&&st[p].r<=r)
{ return st[p].val; }
Push_down(p);
int res = -1,mid = (st[p].l+st[p].r)>>1;
if(l<=mid)
{ res = max(res,query(ls(p),l,r)); }
if(r>mid)
{ res = max(res,query(rs(p),l,r)); }
return res;
}
}Tree;
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s = s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
signed main()
{
//freopen("node.in","r",stdin);
cin >> n;
for(re int i=1,a,b,w; i<=n; i++)
{
p[i] = (node){(cin >> a,a),(cin >> b,b),(cin >> w,w)};
tmp[++cnt] = a,tmp[++cnt] = b;
}
sort(p+1,p+1+n);
sort(tmp+1,tmp+1+cnt);
cnt = unique(tmp+1,tmp+1+cnt)-tmp-1;
for(re int i=1; i<=n; i++)
{
p[i].a = lower_bound(tmp+1,tmp+1+cnt,p[i].a)-tmp;
p[i].b = lower_bound(tmp+1,tmp+1+cnt,p[i].b)-tmp;
//printf("%lld %lld\n",p[i].a,p[i].b);
}
Tree.build(1,1,cnt);
for(re int i=1; i<=n; i++)
{
int tmp = Tree.query(1,1,min(p[i].a,p[i].b));
Tree.update1(1,p[i].a,p[i].b,p[i].w);
Tree.update2(1,p[i].a,p[i].w+tmp);
}
printf("%lld\n",Tree.st[1].val);
/*int ans = 0;
for(re int i=1; i<=n; i++)
{
for(re int j=1; j<=n*2; j++)
{ dp[i][j] = dp[i-1][j]; }
for(re int j=p[i].a; j<=p[i].b; j++)
{ dp[i][j] = max(dp[i][j],dp[i-1][j]+p[i].w); }
for(re int j=1; j<=min(p[i].a,p[i].b); j++)
{ dp[i][p[i].a] = max(dp[i][p[i].a],dp[i-1][j]+p[i].w); }
}
for(re int i=1; i<=n; i++)
{
for(re int j=1; j<=n*2; j++)
{ ans = max(ans,dp[i][j]); }
//printf("\n");
}
printf("%lld\n",ans);*/
return 0;
}
}
signed main()
{ return OMA::main(); }
T3
跑 \(p\) 遍最短路,10pts。
正解:
跑个多源最短路,啥是多源最短路,就是有多个源点,在 \(dij\) 一开始往队列压点的操作时,把源点都压到里边,也就是本题的特殊点,再开个 \(pre\) 数组记录下每个点是由哪个源点扩展过来的,其他都是 \(dij\) 常规操作。
跑完一遍最短路,得到的是某个源点到当前点所构成的最短路径,具体是那个源点,则记录在了 \(pre\) 数组里。
对于答案,我们枚举每一条边,对于边的两个端点,如果其是由两个不同的源点扩展过来的,则可以得到当前两个源点通过 \(\{u,v\}\) 连接的距离 \(dis_{u}+dis_{v}+w\) 。 枚举取最小值即可。
画个图可能更好理解。
Code
#include<queue>
#include<cstdio>
#include<climits>
#include<cstring>
#include<algorithm>
#define MAX 200020
#define re register
#define int long long
#define INF 1145141919810
using std::sort;
using std::priority_queue;
int n,m,p;
int x[MAX];
int ans[MAX];
struct graph
{
int from;
int next;
int to;
int w;
}edge[MAX<<1];
int cnt=1,head[MAX];
inline void add(int u,int v,int w)
{ edge[++cnt] = (graph){u,head[u],v,w},head[u] = cnt; }
namespace MSSP
{
struct my
{
int dis,id;
inline friend bool operator <(const my &a,const my &b)
{ return a.dis>b.dis; }
};
priority_queue<my>q;
bool vis[MAX];
int dis[MAX],pre[MAX];
inline void dijkstra()
{
memset(dis,0x3f,sizeof(dis));
for(re int i=1; i<=p; i++)
{ q.push((my){dis[x[i]] = 0,pre[x[i]] = x[i]}); }
while(!q.empty())
{
int u = q.top().id; q.pop();
if(vis[u])
{ continue ; }
vis[u] = 1;
for(re int i=head[u],v,w; i; i=edge[i].next)
{
v = edge[i].to,w = edge[i].w;
if(dis[v]>dis[u]+w)
{
pre[v] = pre[u];
dis[v] = dis[u]+w;
q.push((my){dis[v],v});
}
}
}
}
}using namespace MSSP;
namespace OMA
{
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
inline int min(int a,int b)
{ return a<b?a:b; }
signed main()
{
//freopen("node.in","r",stdin);
//freopen("my.out","w"i,stdout);
cin >> n >> m >> p;
for(re int i=1; i<=p; i++)
{ cin >> x[i]; ans[x[i]] = INF; }
for(re int i=1,u,v,w; i<=m; i++)
{
cin >> u >> v >> w;
add(u,v,w),add(v,u,w);
}
dijkstra();
for(re int i=2,u,v,w; i<=cnt; i+=2)
{
u = edge[i].from,v = edge[i].to,w = edge[i].w;
if(pre[u]!=pre[v])
{
ans[pre[u]] = min(ans[pre[u]],dis[u]+dis[v]+w);
ans[pre[v]] = min(ans[pre[v]],dis[u]+dis[v]+w);
}
}
for(re int i=1; i<=p; i++)
{ printf("%lld\n",ans[x[i]]); }
return 0;
}
}
signed main()
{ return OMA::main(); }
T4
比较sb的模拟
Solution
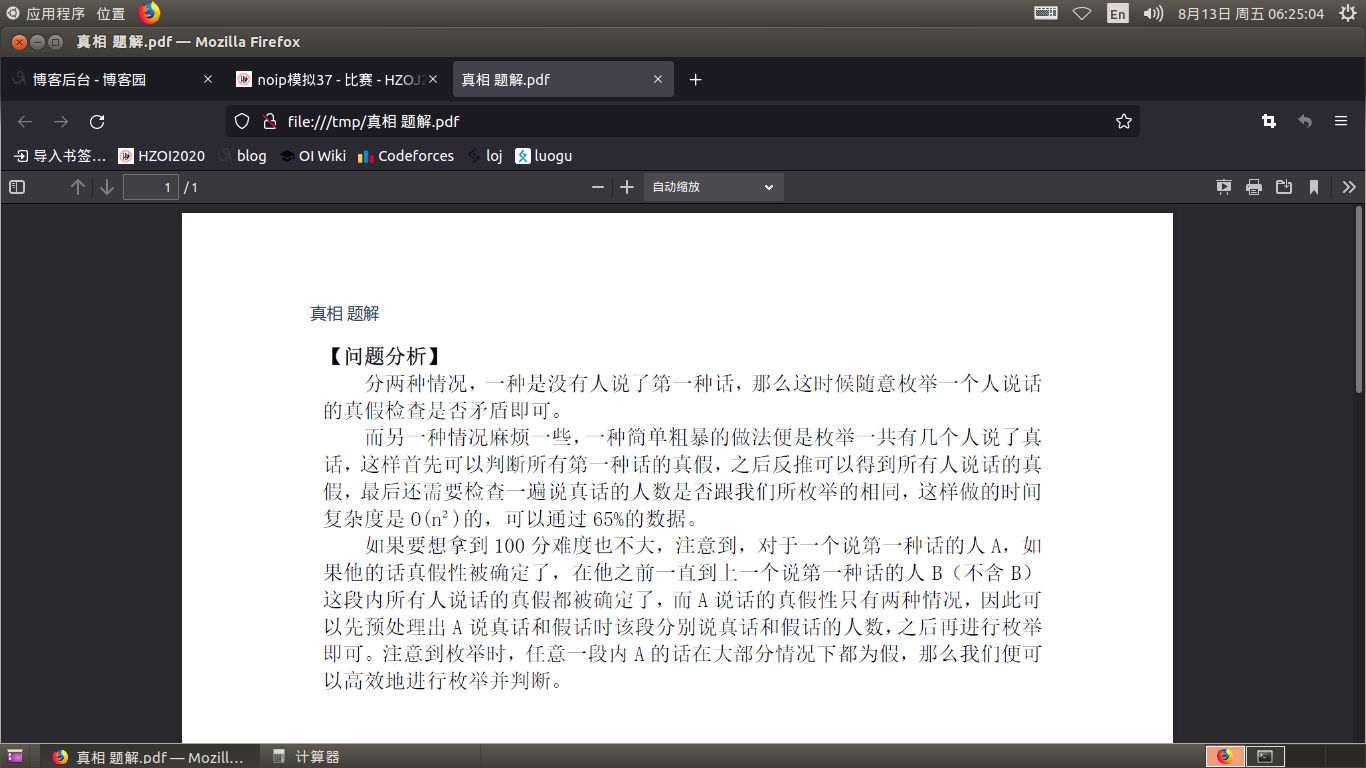
Code
#include<cstdio>
#define MAX 100010
#define re register
namespace OMA
{
int t,n,top,sta[MAX];
int opt[MAX],cnt[MAX],sum,cot;
int rec[MAX],a[MAX][2],b[MAX][2];
signed main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
sum = cot = top = 0;
for(re int i=1; i<=n; i++)
{
char s[5];
scanf("%s",s);
if(s[0]=='$')
{ opt[i] = 1; scanf("%d",&cnt[i]); sta[++top] = i; }
if(s[0]=='+')
{ opt[i] = 2; }
if(s[0]=='-')
{ opt[i] = 3; }
}
if(!top)
{
int jud = 1;
for(re int i=1; i<=n; i++)
{ if(opt[i]==3){ jud ^= 1; } }
if(jud)
{ printf("consistent\n"); }
else
{ printf("inconsistent\n"); }
continue ;
}
for(re int i=1; i<=top; i++)
{
int fr = sta[i]+1,be,tot = 1,truth = 0,jud = 1;
if(i==top)
{ be = sta[1]; }
else
{ be = sta[i+1]; }
if(fr>n)
{ fr -= n; }
for(re int j=fr; j!=be; )
{
if(jud)
{ truth++; }
if(opt[j]==3)
{ jud ^= 1; }
j++,tot++;
if(j>n)
{ j -= n; }
}
rec[++cot] = cnt[be];
if(jud)
{
truth++;
a[cot][0] = tot-truth;
a[cot][1] = truth;
}
else
{
a[cot][0] = truth;
a[cot][1] = tot-truth;
}
b[rec[cot]][0] += a[cot][0];
b[rec[cot]][1] += a[cot][1];
sum += a[cot][0];
}
bool flag = false;
for(re int i=0; i<=n; i++)
{ if(sum-b[i][0]+b[i][1]==i){ flag = true; break ; } }
if(flag)
{ printf("consistent\n"); }
else
{ printf("inconsistent\n"); }
for(re int i=0; i<=n; i++)
{ a[i][0] = a[i][1] = b[i][0] = b[i][1] = 0; }
}
return 0;
}
}
signed main()
{ return OMA::main(); }

