noip36
开场先看一遍题面,凭着错误的感觉t3叫naive是一个原因,312开局。然后就死的很惨。
T1
朴素暴力40pts,细想就有80pts,然而我只写了十分钟左右就爬回T3了,所以...
其实都是借口
正解:
转换一下题意,给定n个非负整数的可重集合,要求满足 \(\sum_{i=1}^{n}x_{i}=m\) ,那么一定有 \(diff\{x_{n}\}\le\sqrt{m}\) ,其中 \(diff\) 表示本质不同的数。
所以用并查集维护一下牌堆之间的关系,用树状数组统计个数即可。
Code
#include<cstdio>
#define MAX 100010
#define re register
#define int long long
namespace OMA
{
int n,m,num;
int w[MAX],p[MAX],cnt[MAX];
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
struct BIT
{
int tree[MAX];
inline int lowbit(int x)
{ return x&-x; }
inline void update(int x,int y)
{
for(re int i=x; i<=n; i+=lowbit(i))
{ tree[i] += y; }
}
inline int query(int x)
{
int res = 0;
for(re int i=x; i; i-=lowbit(i))
{ res += tree[i]; }
return res;
}
}BIT;
inline void modify(int val)
{
for(re int i=p[val]; i<=num-1; i++)
{ w[i] = w[i+1],p[w[i]] = i; }
num--,p[val] = 0;
}
int fa[MAX],size[MAX];
inline int find(int x)
{ return x != fa[x]?fa[x] = find(fa[x]):fa[x]; }
inline void merge(int x,int y)
{
int r1 = find(x),r2 = find(y);
if(r1!=r2)
{
fa[r2] = r1;
BIT.update(size[r1],-1);
BIT.update(size[r2],-1);
if(--cnt[size[r1]]==0)
{ modify(size[r1]); }
if(--cnt[size[r2]]==0)
{ modify(size[r2]); }
size[r1] += size[r2];
BIT.update(size[r1],1);
if(++cnt[size[r1]]==1)
{ w[++num] = size[r1],p[size[r1]] = num; }
}
}
signed main()
{
cin >> n >> m;
for(int i=1; i<=n; i++)
{ fa[i] = i; size[i] = 1; }
BIT.update(1,n);
w[num = 1] = 1,cnt[1] = n;
for(re int i=1,opt; i<=m; i++)
{
cin >> opt;
if(opt==1)
{
int x,y;
cin >> x >> y;
merge(x,y);
}
else
{
int c,ans = 0; cin >> c;
int N = BIT.query(n);
//printf("N=%lld\n",N);
//printf("%lld %lld\n",num,w[num]);
for(re int j=1; j<=num; j++)
{
//printf("j=%lld\n",j);
if(w[j]+c-1>=n)
{ continue ; /*printf("QAQ %lld\n",c);*/ }
//printf("QAQ %lld ",w[j]);
ans += cnt[w[j]]*(N-BIT.query(w[j]+c-1));
if(!c)
{ ans -= cnt[w[j]]*cnt[w[j]]-(cnt[w[j]]-1)*cnt[w[j]]/2; }
}
printf("%lld\n",ans);
}
//printf("i=%lld\n",i);
}
return 0;
}
}
signed main()
{ return OMA::main(); }
T2
咕咕咕
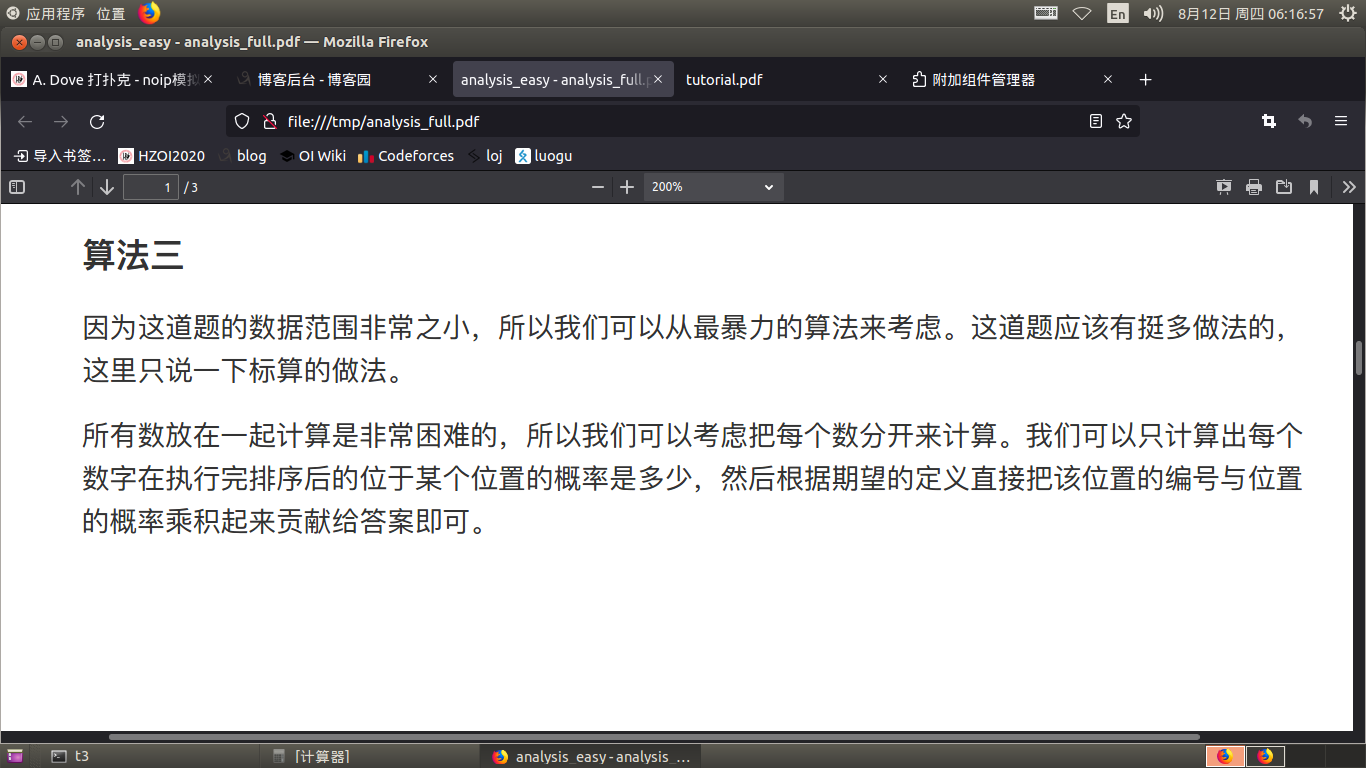
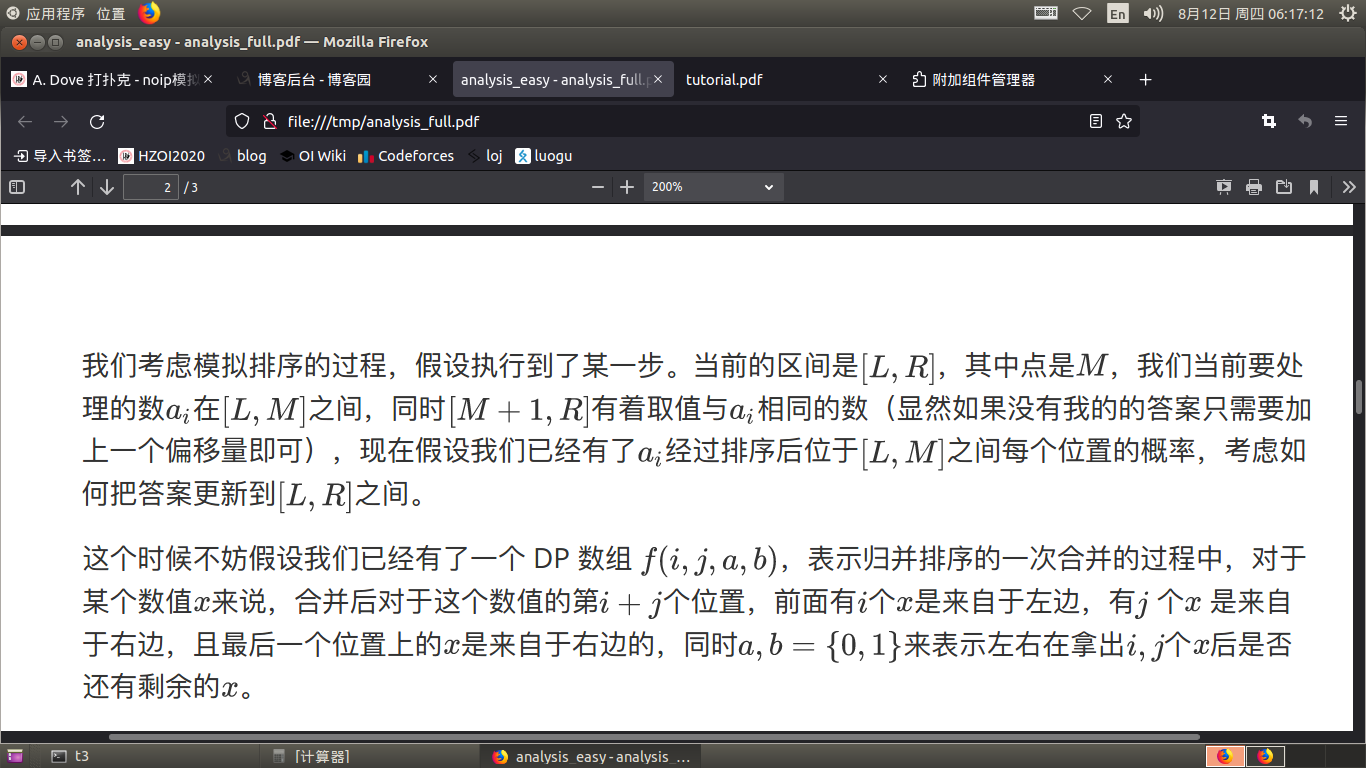
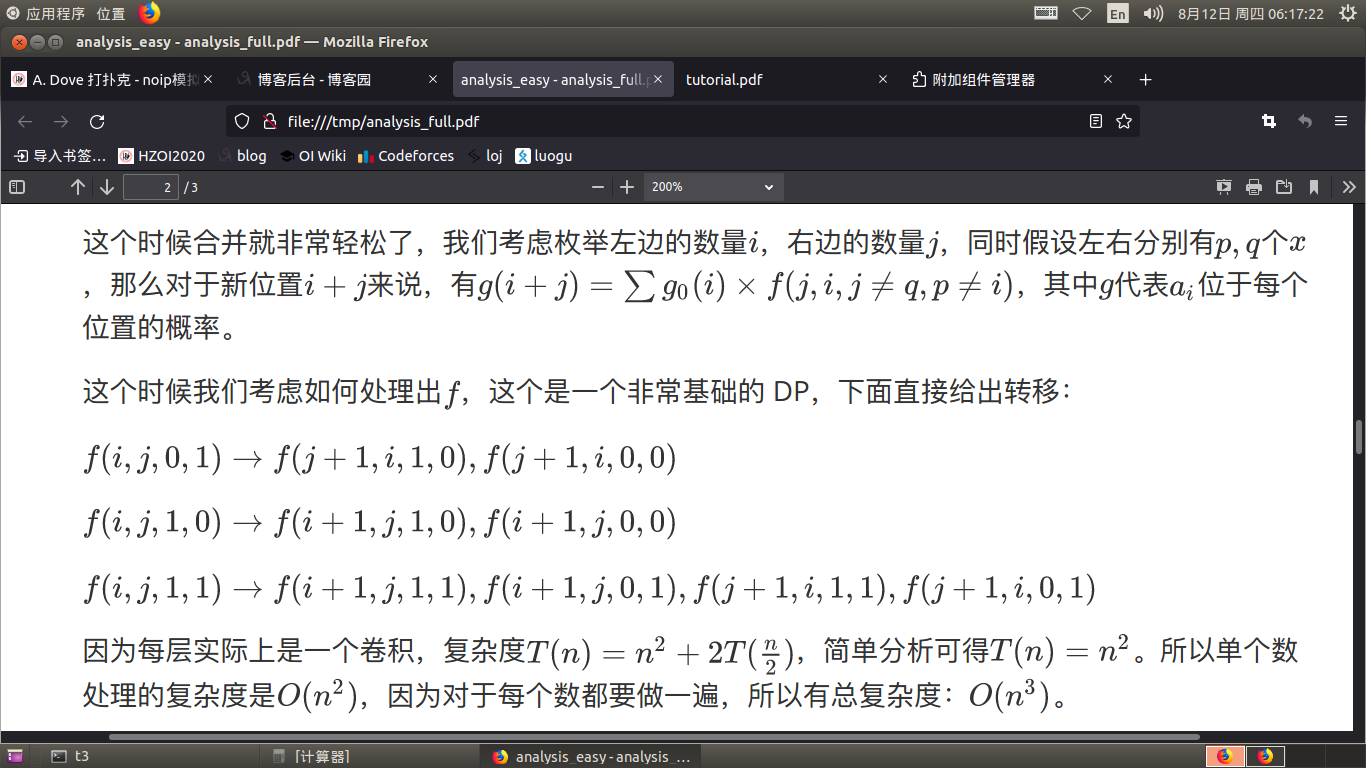
怎么tm不说人话
upd on 08-13
今天T3是个点分治,没学过的我在权衡之下,滚回来改这题。
首先可以根据归并排序的过程和原序列,来得到归并排序的指针移动的概率,设为 \(p_{i,j}\) 表示当前归并排序过程中,两个指针分别指向 \(i,j\) 的概率。
求 \(p\) 数组就是在模拟归并排序的过程。
然后考虑dp,设 \(dp_{dep,i,j}\) 表示当前在归并排序的第 \(dep\) 层, 由 \(i\) 转移到 \(j\) 的概率,有了上边的 \(p\) 数组,就可以直接从 \(dep+1\) 转移到 \(dep\) ,转移时根据 \(a\) 的大小分类讨论。
最后答案直接相乘累加即可。
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 510
#define re register
#define int long long
using std::sort;
namespace OMA
{
int n,a[N];
int p[N][N],dp[N][N][N];
const int mod = 998244353;
const int inv = 499122177;
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
inline void merge_sort(int dep,int l,int r)
{
if(l==r)
{ dp[dep][l][r] = 1; return ; }
int mid = (l+r)>>1;
merge_sort(dep+1,l,mid),merge_sort(dep+1,mid+1,r);
memset(p,0,sizeof(p)); p[0][0] = 1;
for(re int i=0; i<=mid-l+1; i++)
{
for(re int j=0; j<=r-mid; j++)
{
if(i==mid-l+1&&j==r-mid)
{ continue ; }
if(i==mid-l+1)
{ (p[i][j+1] += p[i][j]) %= mod; }
else if(j==r-mid)
{ (p[i+1][j] += p[i][j]) %= mod; }
else if(a[i+l]<a[j+mid+1])
{ (p[i+1][j] += p[i][j]) %= mod; }
else if(a[i+l]>a[j+mid+1])
{ (p[i][j+1] += p[i][j]) %= mod; }
else if(a[i+l]==a[j+mid+1])
{
(p[i+1][j] += p[i][j]*inv%mod) %=mod;
(p[i][j+1] += p[i][j]*inv%mod) %= mod;
}
}
}
for(re int i=l; i<=r; i++)
{
for(re int j=0; j<=mid-l+1; j++)
{
for(re int k=0; k<=r-mid; k++)
{
if(j==mid-l+1&&k==r-mid)
{ continue ; }
if(j==mid-l+1)
{ (dp[dep][i][j+k+l] += dp[dep+1][i][k+mid+1]*p[j][k]%mod) %= mod; }
else if(k==r-mid)
{ (dp[dep][i][j+k+l] += dp[dep+1][i][j+l]*p[j][k]%mod) %= mod; }
else if(a[j+l]<a[k+mid+1])
{ (dp[dep][i][j+k+l] += dp[dep+1][i][j+l]*p[j][k]%mod) %= mod; }
else if(a[j+l]>a[k+mid+1])
{ (dp[dep][i][j+k+l] += dp[dep+1][i][k+mid+1]*p[j][k]%mod) %= mod; }
else if(a[j+l]==a[k+mid+1])
{
(dp[dep][i][j+k+l] += dp[dep+1][i][j+l]*p[j][k]%mod*inv%mod) %= mod;
(dp[dep][i][j+k+l] += dp[dep+1][i][k+mid+1]*p[j][k]%mod*inv%mod) %= mod;
}
}
}
}
sort(a+l,a+r+1);
}
signed main()
{
cin >> n;
for(re int i=1; i<=n; i++)
{ cin >> a[i]; }
merge_sort(1,1,n);
for(re int i=1,ans; i<=n; i++)
{
ans = 0;
for(re int j=1; j<=n; j++)
{ (ans += j*dp[1][i][j]%mod) %= mod; }
printf("%lld ",ans);
}
return 0;
}
}
signed main()
{ return OMA::main(); }
T3
一直在写,然而分并不高。
因为一直在用错误的思路,上厕所的时候还把自己搞掉了,然而回来后,继续乱搞。
乱搞:
测试点b分治
首先写个 \(O(n^2)\) 暴力,发现 \(n\le30000\) 随便跑,然后我们大胆一些其实是经由某b试出来的,当当前算出的\(r-l+1>700\) 时,停止枚举 \(r\) ,直接去更新答案。
没有正确性,但是能A。大雾。
正解:
st表+链表。
我们固定右端点,枚举左端点来考虑。
对于本题,有几个比较关键的性质:
- \(OR-AND\) 本质不同的位置有 \(2\log n\) 个,且本质相同的位置都是连续的
- \(OR-AND\) 递增
- \(MIN-MAX\) 递减
对于1,考虑 \(OR\) 的后缀和 \(suf_{i}\) ,对于任意一个满足 \(suf_{i}\neq sud_{i+1}\) 的位置,\(suf_{i+1}\) 相较于\(suf_{i}\) 必然是至少有一位由 0 变成了 1 。总的二进制位数为 \(log\) 级别,所以 \(OR\) 本质不同的位置共有 \(log n\) 个,\(AND\) 同理,所以 \(OR-AND\) 本质不同的位置共有 \(2log n\) 个。
实在不懂,可以手模一下,就明白了。
2,3很好理解,就不再说了。
当移动右端点时,考虑用链表来记录下左端点所有 \(OR-AND\) 不同的区段,就是用链表记录一下右端点,对于 \(OR-AND\) 相等的一段,\(MIN-MAX\) 是递减的,所以直接二分来搞,\(O(nlog^{2} n)\) 。
因为我们要找的是最长的,所以找到第一个合法的直接break掉即可,\(O(nlog n)\)
再用线段树维护一下答案,最后遍历叶子结点输出答案即可。
具体实现见code。
Code
#include<list>
#include<cstdio>
#define re register
#define MAX 1000100
using std::list;
int n,k,a[MAX];
struct node
{
int p,ro,dna;
inline int delta()
{ return ro-dna; }
};
list<node>LIST;
inline int max(int a,int b)
{ return a>b?a:b; }
inline int min(int a,int b)
{ return a<b?a:b; }
namespace ST
{
int log[MAX];
int f[MAX][20],g[MAX][20]; // xam,nim
inline void pre_work()
{
for(re int i=2; i<=n; i++)
{ log[i] = log[i>>1]+1; }
for(re int j=1; j<=log[n]; j++)
{
for(re int i=1; i<=n-(1<<j)+1; i++)
{
f[i][j] = max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
g[i][j] = min(g[i][j-1],g[i+(1<<(j-1))][j-1]);
}
}
}
inline int query1(int l,int r)
{
int gol = log[r-l+1];
return max(f[l][gol],f[r-(1<<gol)+1][gol]);
}
inline int query2(int l,int r)
{
int gol = log[r-l+1];
return min(g[l][gol],g[r-(1<<gol)+1][gol]);
}
}using namespace ST;
namespace OMA
{
struct Segment_Tree
{
struct TREE
{ int l,r,len; }st[MAX<<2];
inline int ls(int p)
{ return p<<1; }
inline int rs(int p)
{ return p<<1|1; }
inline void build(int p,int l,int r)
{
st[p] = (TREE){l,r,-1};
if(l==r)
{ return ; }
int mid = (l+r)>>1;
build(ls(p),l,mid),build(rs(p),mid+1,r);
}
inline void update(int p,int l,int r)
{
if(l<=st[p].l&&st[p].r<=r)
{
st[p].len = max(st[p].len,r-l+1);
return ;
}
int mid = (st[p].l+st[p].r)>>1;
if(l<=mid)
{ update(ls(p),l,r); }
if(r>mid)
{ update(rs(p),l,r); }
}
inline void print(int p)
{
if(st[p].l==st[p].r)
{ printf("%d ",st[p].len); return ; }
st[ls(p)].len = max(st[ls(p)].len,st[p].len);
st[rs(p)].len = max(st[rs(p)].len,st[p].len);
print(ls(p)),print(rs(p));
}
}Tree;
struct stream
{
template<typename type>inline stream &operator >>(type &s)
{
int w=1; s=0; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*=w,*this;
}
}cin;
inline bool check(list<node>::iterator it,int l,int r)
{ /*printf("check %d %d\n",l,r);*/ return it->delta()+query2(l,r)-query1(l,r)>=k; }
signed main()
{
//freopen("data.in","r",stdin);
//freopen("my.out","w",stdout);
cin >> n >> k;
for(re int i=1; i<=n; i++)
{ f[i][0] = g[i][0] = (cin >> a[i],a[i]); }
pre_work(); Tree.build(1,1,n);
//printf("???\n");
for(re int i=1; i<=n; i++)
{
//printf("one\n");
for(auto it=LIST.begin(); it!=LIST.end(); it++)
{ it->ro |= a[i],it->dna &= a[i]; /*printf("??1\n");*/ }
//printf("two\n");
LIST.emplace_back((node){i,a[i],a[i]});
//printf("i=%d\n",i);
//printf("three\n");
for(auto it1=LIST.begin(),it2=next(it1); it2!=LIST.end(); it2++)
{
//printf("???2\n");
if(it1->delta()==it2->delta())
{ LIST.erase(it1); it1 = it2; }
else
{ ++it1; }
}
//printf("four\n");
for(auto it=LIST.begin(); it!=LIST.end(); it++)
{
//printf("QAQ\n");
if(check(it,it->p,i))
{
//printf("five\n");
int l = 1,r = it->p,res;
if(it!=LIST.begin())
{ l = prev(it)->p+1; }
while(l<=r)
{
int mid = (l+r)>>1;
if(check(it,mid,i))
{ r = mid-1,res = mid; }
else
{ l = mid+1; }
}
Tree.update(1,res,i);
break ;
}
}
//printf("end:%d\n",i);
}
Tree.print(1);
return 0;
}
}
signed main()
{ return OMA::main(); }
反思总结:
- 不要硬刚一道题,时间分配要有比重。
- 当前思路不可做,就换一种,哪怕是乱搞。
- 一些能优化的地方尽量去优化,不要直接冲傻瓜暴力。
不过话说这次读题没啥问题

