noip22
T1
考试的时候打的特殊性质分,然而暴力竟然写假了。
正解:
显然是个贪心,要最大化 \(a_{\min}\times b_{\min}\),肯定是要删掉若干个 \(a\) 最小,\(b\) 最小的矩形。但直接去枚举显然会T掉。
考虑如何去优化这个过程,我们可以先按 \(a\) 单关键字从小到达 排序一下。 先删掉前m个 \(a\) 小的,将剩下的全压进堆里,堆按 \(b\) 从小到达 排序,之后从m开始倒序枚举,将当前的矩形压到堆里,再将堆顶元素弹出,然后统计答案。
详见code。
Code
#include<queue>
#include<cstdio>
#include<algorithm>
#define MAX 100010
#define re register
#define int long long
namespace OMA
{
int t,n,m,ans;
bool vis[MAX];
struct martix
{
int a,b;
inline friend bool operator <(const martix &a,const martix &b)
{ return a.b>b.b; }
}ar[MAX];
std::priority_queue<martix>q;
inline bool cmp(const martix &a,const martix &b)
{ return a.a<b.a; }
inline int read()
{
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
inline int max(int a,int b)
{ return a>b?a:b; }
signed main()
{
t = read();
while(t--)
{
int mina,minb;
ans = 0,n = read(),m = read();
for(re int i=1; i<=n; i++)
{ ar[i] = (martix){read(),read()}; }
std::sort(ar+1,ar+1+n,cmp);
for(re int i=m+1; i<=n; i++)
{ q.push(ar[i]); }
mina = ar[m+1].a,minb = q.top().b;
ans = mina*minb;
for(re int i=m; i; i--)
{
q.push(ar[i]),q.pop();
mina = ar[i].a,minb = q.top().b;
ans = max(ans,mina*minb);
}
while(!q.empty())
{ q.pop(); }
printf("%lld\n",ans);
}
return 0;
}
}
signed main()
{ return OMA::main(); }
如果看了的话,可能会有一个问题,如果当前元素压到堆里,删除的也是它,却还拿它来更新答案,不会错吗? 显然,如果这样的话,这个矩形肯定不是我们要留下来的,所以不会将答案更新。
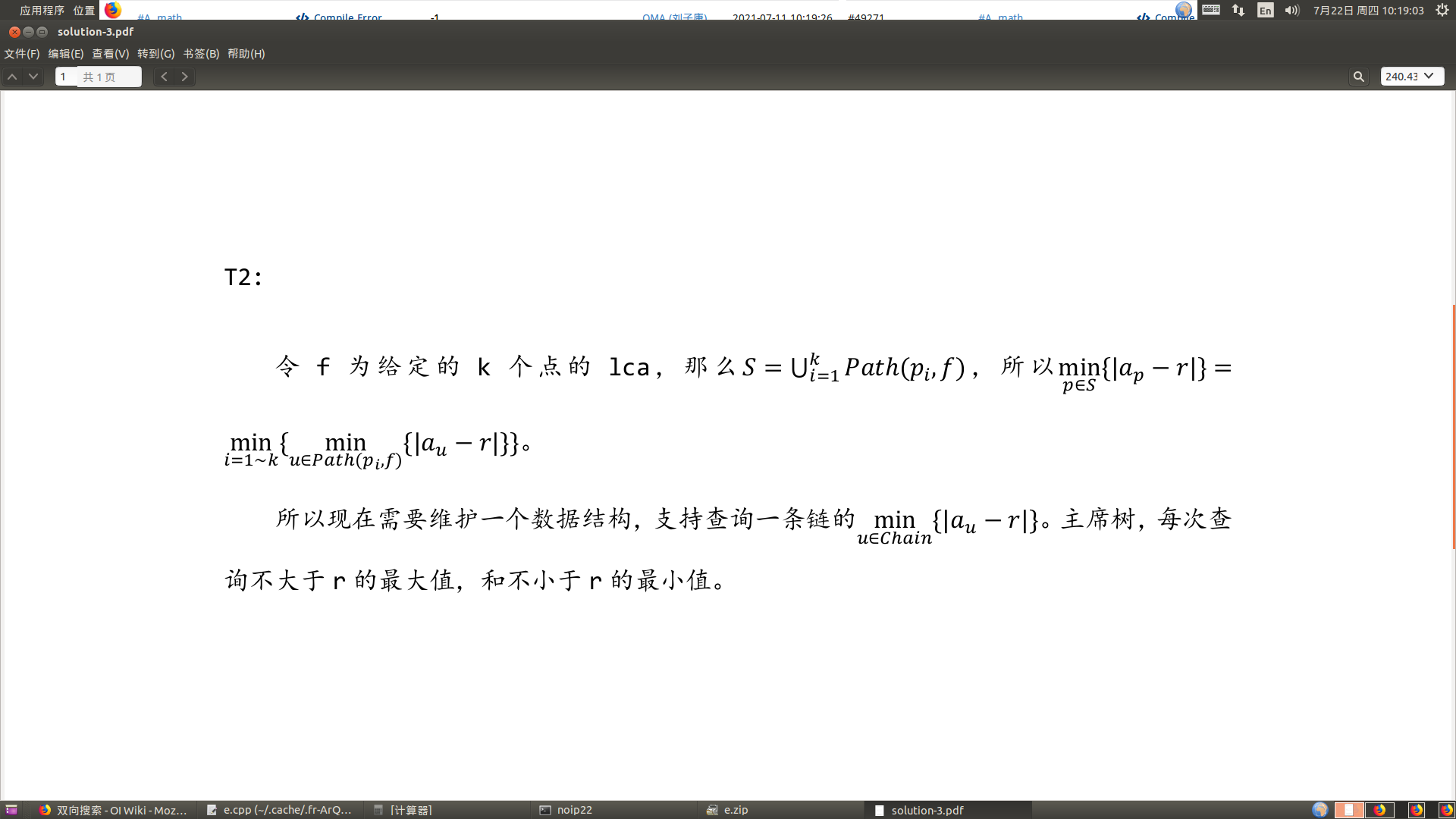
T2
考试的时候同样打的特殊性质分,然而暴搜写假了,前两个点没拿分。
正解是主席树,但本人太菜,不会。所以...
std
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10,inf=1e9,size=maxn*40;
int n,q,type,a[maxn],lastans,r,k,p[maxn],fa[20][maxn],dep[maxn],rt[maxn];
vector<int> g[maxn];
namespace segt{
int cnt,sum[size],lson[size],rson[size];
inline int newnode(int x){
++cnt;
sum[cnt]=sum[x];
lson[cnt]=lson[x];rson[cnt]=rson[x];
return cnt;
}
inline void push_up(int rt){
sum[rt]=sum[lson[rt]]+sum[rson[rt]];
}
int insert(int rt,int l,int r,int pos){
rt=newnode(rt);
++sum[rt];
if(l==r)
return rt;
int mid=l+r>>1;
if(pos<=mid)
lson[rt]=insert(lson[rt],l,mid,pos);
else
rson[rt]=insert(rson[rt],mid+1,r,pos);
push_up(rt);
return rt;
}
int queryl(int rt1,int rt2,int l,int r,int y){
if(sum[rt1]==sum[rt2])
return 0;
if(l==r)
return l;
int mid=l+r>>1;
if(y<=mid)
return queryl(lson[rt1],lson[rt2],l,mid,y);
else{
int tmp=queryl(rson[rt1],rson[rt2],mid+1,r,y);
if(tmp)
return tmp;
else
return queryl(lson[rt1],lson[rt2],l,mid,mid);
}
}
int queryr(int rt1,int rt2,int l,int r,int x){
if(sum[rt1]==sum[rt2])
return 0;
if(l==r)
return l;
int mid=l+r>>1;
if(x>mid)
return queryr(rson[rt1],rson[rt2],mid+1,r,x);
else{
int tmp=queryr(lson[rt1],lson[rt2],l,mid,x);
if(tmp)
return tmp;
else
return queryr(rson[rt1],rson[rt2],mid+1,r,mid+1);
}
}
}
void dfs(int pos){
for(int i=1;i<20;++i)
fa[i][pos]=fa[i-1][fa[i-1][pos]];
dep[pos]=dep[fa[0][pos]]+1;
rt[pos]=segt::insert(rt[fa[0][pos]],1,inf,a[pos]);
for(int i=0;i<g[pos].size();++i)
if(g[pos][i]!=fa[0][pos]){
fa[0][g[pos][i]]=pos;
dfs(g[pos][i]);
}
}
inline int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=19;~i;--i)
if(dep[fa[i][u]]>=dep[v])
u=fa[i][u];
if(u==v)
return u;
for(int i=19;~i;--i)
if(fa[i][u]!=fa[i][v])
u=fa[i][u],v=fa[i][v];
return fa[0][u];
}
int main(){
freopen("e.in","r",stdin);
freopen("e.out","w",stdout);
scanf("%d%d%d",&n,&q,&type);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
for(int i=1,u,v;i<n;++i){
scanf("%d%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1);
while(q--){
scanf("%d%d",&r,&k);
for(int i=1;i<=k;++i){
scanf("%d",&p[i]);
p[i]=(p[i]-1+lastans*type)%n+1;
}
int f=p[1],res=inf;
for(int i=2;i<=k;++i)
f=lca(f,p[i]);
f=fa[0][f];
for(int i=1,tmp;i<=k;++i){
tmp=segt::queryl(rt[f],rt[p[i]],1,inf,r);
if(tmp&&r-tmp<res)
res=r-tmp;
tmp=segt::queryr(rt[f],rt[p[i]],1,inf,r);
if(tmp&&tmp-r<res)
res=tmp-r;
}
printf("%d\n",res);
lastans=res;
}
return 0;
}
所以已经好几场都有主席树了,为什么还不去学啊涉及到的都没改出来QAQ
所以我决定去按考场思路来写,先树剖,然后线段树维护。但当时脑抽,一看维护差值就没打。
其实很好解决,只要查找 \(r\) 在当前这个点到公共 \(LCA\) 这条链上的前驱后继即可,所以考虑平衡树。
一条链可以用dfn序转换为序列上的问题,所以外层套个线段树,内层套平衡树,查询的时候再按树剖的查询方式来查前驱后继即可。
思路很简单,代码很好写指291行的代码,也很好调,直接冲板子即可。
如果你真的码了的话,发现T了链的那个点,很好解决,特判即可。
不过应该会被蒲公英图卡死,所以主席树还是要学的。
好吧,我还是去学了QAQ
所以这是叫树套树套树吗
Code
#include<time.h>
#include<cstdio>
#include<stdlib.h>
#define MAX 100010
#define re register
namespace OMA
{
int n,q,type,last,lca;
int r,k,a[MAX],p[MAX];
struct Graph
{
int next;
int to;
}edge[MAX<<1];
int cnt=1,head[MAX];
inline void add(int u,int v)
{
edge[++cnt].next = head[u];
edge[cnt].to = v;
head[u] = cnt;
}
int fa[MAX],son[MAX];
int dep[MAX],size[MAX];
int top[MAX],dfn[MAX],id[MAX];
inline void dfs1(int u,int fat,int depth)
{
fa[u] = fat;
size[u] = 1;
dep[u] = depth;
for(re int i=head[u]; i; i=edge[i].next)
{
int v = edge[i].to;
if(v!=fat)
{
dfs1(v,u,depth+1);
size[u] += size[v];
if(!son[u]||size[v]>size[son[u]])
{ son[u] = v; }
}
}
}
inline void dfs2(int u,int t)
{
top[u] = t;
id[dfn[u] = ++cnt] = a[u];
if(son[u])
{ dfs2(son[u],t); }
for(re int i=head[u]; i; i=edge[i].next)
{
int v = edge[i].to;
if(v!=fa[u]&&v!=son[u])
{ dfs2(v,v); }
}
}
inline int LCA(int a,int b)
{
while(top[a]!=top[b])
{
if(dep[top[a]]>dep[top[b]])
{ a = fa[top[a]]; }
else
{ b = fa[top[b]]; }
}
return dep[a]<dep[b]?a:b;
}
inline int max(int a,int b)
{ return a>b?a:b; }
inline int min(int a,int b)
{ return a<b?a:b; }
struct Segment_Tree
{
struct TREE
{ int l,r,rt; }st[MAX<<2];
struct FHQ_Treap
{
int tot;
struct TREE
{
int size;
int ls,rs;
int key,val;
}bst[MAX*20];
inline void Push_up(int p)
{ bst[p].size = bst[bst[p].ls].size+bst[bst[p].rs].size+1; }
inline int new_pot(int val)
{
bst[++tot].val = val;
bst[tot].size = 1;
bst[tot].key = rand();
return tot;
}
inline void split(int p,int val,int &p1,int &p2)
{
if(!p)
{ p1 = p2 = 0; return ; }
if(bst[p].val<=val)
{ split(bst[p1 = p].rs,val,bst[p].rs,p2); }
else
{ split(bst[p2 = p].ls,val,p1,bst[p].ls); }
Push_up(p);
}
inline int merge(int p1,int p2)
{
if(!p1||!p2)
{ return p1|p2; }
if(bst[p1].key<bst[p2].key)
{
bst[p1].rs = merge(bst[p1].rs,p2);
Push_up(p1);
return p1;
}
else
{
bst[p2].ls = merge(p1,bst[p2].ls);
Push_up(p2);
return p2;
}
}
inline void insert(int &root,int val)
{
int p1 = 0,p2 = 0;
split(root,val,p1,p2);
root = merge(merge(p1,new_pot(val)),p2);
}
inline int pre(int &root,int val)
{
int p1 = 0,p2 = 0;
split(root,val,p1,p2);
if(!p1)
{ return -0x7f7f7f7f; }
int p = p1;
while(bst[p].rs)
{ p = bst[p].rs; }
root = merge(p1,p2);
return bst[p].val;
}
inline int suf(int &root,int val)
{
int p1 = 0,p2 = 0;
split(root,val-1,p1,p2);
int p = p2;
if(!p2)
{ return 0x7f7f7f7f; }
while(bst[p].ls)
{ p = bst[p].ls; }
root = merge(p1,p2);
return bst[p].val;
}
}Treap;
inline int ls(int p)
{ return p<<1; }
inline int rs(int p)
{ return p<<1|1; }
inline void build(int p,int l,int r)
{
st[p].l = l,st[p].r = r;
if(l==r)
{ st[p].rt = Treap.new_pot(id[l]); return ; }
for(re int i=l; i<=r; i++)
{ Treap.insert(st[p].rt,id[i]); }
int mid = (l+r)>>1;
build(ls(p),l,mid),build(rs(p),mid+1,r);
}
inline int Pre(int p,int l,int r,int val)
{
if(l<=st[p].l&&st[p].r<=r)
{ return Treap.pre(st[p].rt,val); }
int pre = -0x7f7f7f7f,mid = (st[p].l+st[p].r)>>1;
if(l<=mid)
{ pre = max(pre,Pre(ls(p),l,r,val)); }
if(r>mid)
{ pre = max(pre,Pre(rs(p),l,r,val)); }
return pre;
}
inline int Suf(int p,int l,int r,int val)
{
if(l<=st[p].l&&st[p].r<=r)
{ return Treap.suf(st[p].rt,val); }
int suf = 0x7f7f7f7f,mid = (st[p].l+st[p].r)>>1;
if(l<=mid)
{ suf = min(suf,Suf(ls(p),l,r,val)); }
if(r>mid)
{ suf = min(suf,Suf(rs(p),l,r,val)); }
return suf;
}
inline void swap(int &a,int &b)
{ int t=a; a=b; b=t; }
inline int PRE(int a,int b)
{
int pre = -0x7f7f7f7f;
while(top[a]!=top[b])
{
if(dep[top[a]]<dep[top[b]])
{ swap(a,b); }
pre = max(pre,Pre(1,dfn[top[a]],dfn[a],r));
a = fa[top[a]];
}
if(dep[a]>dep[b])
{ swap(a,b); }
pre = max(pre,Pre(1,dfn[a],dfn[b],r));
return pre;
}
inline int SUF(int a,int b)
{
int suf = 0x7f7f7f7f;
while(top[a]!=top[b])
{
if(dep[top[a]]<dep[top[b]])
{ swap(a,b); }
suf = min(suf,Suf(1,dfn[top[a]],dfn[a],r));
a = fa[top[a]];
}
if(dep[a]>dep[b])
{ swap(a,b); }
suf = min(suf,Suf(1,dfn[a],dfn[b],r));
return suf;
}
}Tree;
inline int read()
{
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
inline int abs(int a)
{ return a>=0?a:-a; }
signed main()
{
//freopen("node.in","r",stdin);
//freopen("my.out","w",stdout);
srand(time(NULL));
n = read(),q = read(),type = read();
for(re int i=1; i<=n; i++)
{ a[i] = read(); }
bool flag = true;
for(re int i=1,u,v; i<=n-1; i++)
{
u = read(),v = read();
add(u,v),add(v,u);
if(v!=u+1)
{ flag = false; }
}
if(flag)
{
for(re int i=1; i<=q; i++)
{
int ans = 0x7f7f7f7f;
int L = 0x3f3f3f3f,R = 0;
r = read(),k = read();
for(re int j=1; j<=k; j++)
{ p[j] = (read()-1+last*type)%n+1; L = min(L,p[j]),R = max(R,p[j]); }
for(re int j=L; j<=R; j++)
{ ans = min(ans,abs(a[j]-r)); if(!ans){ break ; }}
printf("%d\n",ans);
}
return 0;
}
dfs1(1,0,0),cnt = 0,dfs2(1,1);
Tree.build(1,1,n);
for(re int i=1; i<=q; i++)
{
int ans = 0x7f7f7f7f;
r = read(),k = read();
for(re int j=1; j<=k; j++)
{ p[j] = (read()-1+last*type)%n+1; }
lca = p[1];
for(re int j=2; j<=k; j++)
{ lca = LCA(lca,p[j]); }
//printf("LCA=%d\n",lca);
for(re int j=1; j<=k; j++)
{
int pre = Tree.PRE(p[j],lca);
int suf = Tree.SUF(p[j],lca);
//printf("pre=%d suf=%d\n",pre,suf);
if(!pre)
{ pre = 0x7f7f7f7f; }
if(!suf)
{ suf = 0x7f7f7f7f; }
ans = min(ans,min(abs(pre-r),abs(suf-r)));
if(!ans)
{ break ; }
}
last = ans;
printf("%d\n",ans);
}
return 0;
}
}
signed main()
{ return OMA::main(); }
T3
为什么我直接冲暴力都只能拿特判分啊
果然还是太菜了
正解:
还在改,先咕了话说,场场咕t3真的好吗QAQ
所以....



 浙公网安备 33010602011771号
浙公网安备 33010602011771号