noip20
T1
首先,这个插球,就是森林中连点,考虑dp,我们设 \(dp_{i,j}\) 表示有i个点的森林,有j个点在第一颗树中的概率,转移时考虑第i个点是否在第一颗子树里,转移方程:
\[dp_{i,j}=dp_{i-1,j-1}\times (j-1)\times inv_{i}+dp_{i-1,j}\times (i-j)\times inv_{i}
\]
设 \(f_{i,j}\) 表示有i个的树,深度不超过j的概率,\(g_{i,j}\) 表示有i个点的森林,深度不超过j的概率,转移方程为:
\[f_{i,j}=g_{i-1,j-1}
\]
\[g_{i,j}=\sum_{k=1}^{i} f_{k,j}\times g_{i-k,j}\times dp_{i,k}
\]
比较恶心的是初始化,按照定义来初始化就好,就是容易漏情况,具体看code。
注意取模QAQ
Code
#include<cstdio>
#define N 220
#define re register
#define int long long
namespace OMA
{
int n,p,inv[N],sum;
int dp[N][N],f[N][N],g[N][N];
inline int quickpow(int a,int b)
{
int ans = 1;
while(b)
{
if(b&1)
{ ans = ans*a%p; }
a = a*a%p;
b >>= 1;
}
return ans;
}
signed main()
{
scanf("%lld%lld",&n,&p);
dp[1][1] = dp[1][0] = 1;
inv[0] = 1,inv[n] = quickpow(n,p-2);
for(re int i=n-1; i>=1; i--)
{ inv[i] = quickpow(i,p-2); }
for(re int i=2; i<=n; i++)
{
for(re int j=1; j<=i; j++)
{ dp[i][j] = ((dp[i-1][j-1]*(j-1)%p*inv[i]%p+dp[i-1][j]*(i-j)%p*inv[i]%p)%p+p)%p; }
}
for(re int i=0; i<=n; i++)
{ f[0][i] = g[0][i] = 1; }
for(re int i=1; i<=n; i++)
{
for(re int j=i-1; j<=n; j++)
{ f[i][j] = g[i][j] = 1; }
}
for(re int i=2; i<=n; i++)
{
for(re int j=0; j<=i-2; j++)
{
if(j)
{ f[i][j] = g[i-1][j-1]; }
for(re int k=1; k<=i; k++)
{ (g[i][j] += f[k][j]*g[i-k][j]%p*dp[i][k]%p) %= p; }
}
}
for(re int i=1; i<=n; i++)
{ (sum += ((f[n][i]-f[n][i-1])*i%p+p)%p) %= p; }
printf("%lld\n",sum);
return 0;
}
}
signed main()
{ return OMA::main(); }
T2
考试的时候想骗 \(c=0\) 的点,结果挂了,
90 1 19
16 79 0
傻逼数据,1不连边
记搜有72pts..
TLE 72pts
#include<bitset>
#include<cstdio>
#define re register
const int N = 111;
const int M = 8500;
namespace OMA
{
int n,m,d,ans;
struct graph
{
int next;
int to;
int w;
}edge[M<<1];
int staa[1<<21];
std::bitset<1<<20>vis[N][N];
int cnt=1,head[N];
inline int read()
{
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
inline void add(int u,int v,int w)
{
edge[++cnt].next = head[u];
edge[cnt].to = v;
edge[cnt].w = w;
head[u] = cnt;
}
inline void dfs(int u,int sta,int dnt)
{
if(vis[u][dnt][sta])
{ return ; }
if(dnt==d)
{ if(!staa[sta]){ ans++,staa[sta] = 1; } return ; }
vis[u][dnt][sta] = 1;
for(re int i=head[u]; i; i=edge[i].next)
{
int v = edge[i].to,w = edge[i].w;
int stat = sta|(w<<dnt);
dfs(v,stat,dnt+1);
}
}
signed main()
{
n = read(),m = read(),d = read();
for(re int i=1,u,v,w; i<=m; i++)
{
u = read(),v = read(),w = read();
add(u,v,w),add(v,u,w);
}
dfs(1,0,0);
printf("%d\n",ans);
return 0;
}
}
signed main()
{ return OMA::main(); }
正解:
显然是状压,设 \(dp_{i,j,mask}\) 表示从i出发,到j结束,是否存在一条状态为mask的路径,最后枚举转移答案,但直接转移会T掉题解里说的,考虑如何优化
具体实现可见代码。
时间复杂度 \(O(2^{\frac{d}{2}}\times n\times (n+m)+2^{d}\times n)\)
也是题解里说的
Code
#include<bitset>
#include<cstdio>
#include<cstring>
#define re register
const int N = 221;
const int M = 8500;
const int MASK = 1<<10+1;
namespace OMA
{
int n,m,d[3],ans;
std::bitset<N>dp[MASK][2],link[N][2];
inline int read()
{
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
signed main()
{
n = read(),m = read(),d[0] = read();
for(re int i=1,u,v,w; i<=m; i++)
{
u = read(),v = read(),w = read();
link[u][w][v] = link[v][w][u] = 1;
}
d[2] = d[0]-(d[1] = d[0]/2);
int mask[2] = {1<<d[1],1<<d[2]};
for(re int u=n; u; u--)
{
for(re int i=0; i<MASK; i++)
{ dp[i][0].reset(); }
dp[1][0][u] = 1;
for(re int i=0; i<=mask[1]-1; i++)
{
for(re int v=1; v<=n; v++)
{
if(dp[i][0][v])
{ dp[i<<1][0] |= link[v][0],dp[i<<1|1][0] |= link[v][1]; }
}
}
for(re int i=0; i<=mask[1]-1; i++)
{ dp[i][1][u] = dp[mask[1]|i][0].any(); }
}
for(re int i=0; i<=mask[1]-1; i++)
{
for(re int j=0; j<=mask[0]-1; j++)
{
if((dp[mask[0]|j][0]&dp[i][1]).any())
{ ans++; }
}
}
printf("%d\n",ans);
return 0;
}
}
signed main()
{ return OMA::main(); }
T3
暴力30pts+ \(q=0\) 1pts+单调14pts
单调包括递增和递减,注意一下。
45pts
#include<cmath>
#include<cstdio>
#define MAX 100100
#define re register
#define int long long
namespace OMA
{
int n,q;
int x[MAX],len[MAX];
inline int read()
{
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-')w=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ s=s*10+ch-'0'; ch=getchar(); }
return s*w;
}
inline int abs(int a)
{ return a>=0?a:-a; }
inline void task1()
{
int l,r;
long long cast;
for(re int i=1; i<=q; i++)
{
cast = l = 0,r = len[i];
for(re int j=1; j<=n; j++)
{
//printf("l=%d r=%d to=%d ",l,r,x[j]);
if((r>x[j]&&l<x[j])||(r==x[j])||(l==x[j]))
{ continue ; }
else if(abs(r-x[j])<abs(l-x[j]))
{ cast += abs(r-x[j]),r = x[j],l = r-len[i]; }
else
{ cast += abs(l-x[j]),l = x[j],r = l+len[i]; }
//printf("haven casted:%d\n",cast);
}
printf("%lld\n",cast);
}
}
inline void task2()
{
int cnt[2] = {0,0}; // up down
for(re int i=2; i<=n; i++)
{
if(x[i]>x[i-1])
{ cnt[0]++; }
else if(x[i]<x[i-1])
{ cnt[1]++; }
}
if(cnt[0]==n-1)
{
if(x[1]>=0)
{
for(re int i=1; i<=q; i++)
{ printf("%lld\n",(len[i]<x[n])?(x[n]-len[i]):0); }
}
else
{
for(re int i=1; i<=q; i++)
{ printf("%lld\n",abs(x[1])+abs(x[n]-x[1]-len[i])); }
}
}
if(cnt[1]==n-1)
{
for(re int i=1; i<=q; i++)
{
int cast = 0;
if(x[1]>len[i])
{ cast = x[1]-len[i]; }
if(x[n]<cast)
{ cast += cast-x[n]; }
printf("%lld\n",cast);
}
}
}
inline void task3()
{ ; }
inline void task4()
{ ; }
signed main()
{
//freopen("node.in","r",stdin);
//freopen("my.out","w",stdout);
n = read(),q = read();
for(re int i=1; i<=n; i++)
{ x[i] = read(); }
for(re int i=1; i<=q; i++)
{ len[i] = read(); }
if(q==0)
{ return 0; }
if(n<=1e3)
{ task1(); }
else
{
task2();
//task3();
//task4();
}
return 0;
}
}
signed main()
{ return OMA::main(); }
正解不会...,所以,
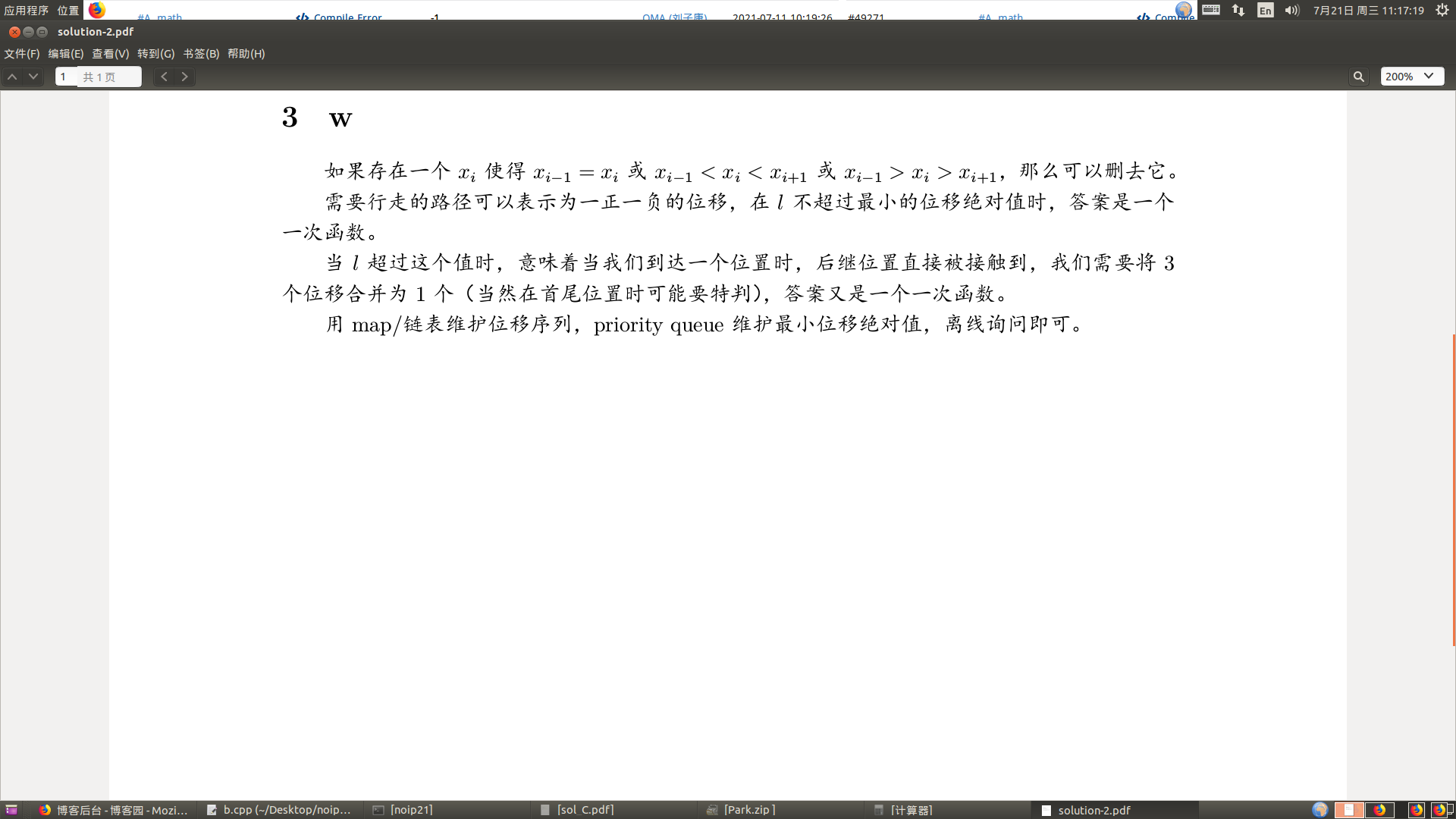
所以为什么给的std只能拿30pts啊,单调还判错了
updated on 7.21
好吧,std换成对的了 是指针好吧,是迭代器,可恶
没改出来,贴下std吧..
std
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
int n,m;
ll tot,ans[maxn];
vector<int> x;
vector<pair<int,int> > a;
map<int,int> mp;
inline ll calc(ll k){
if(!mp.empty()&&mp.begin()->second<0)
return tot-(mp.size()-1)*k;
else
return tot-mp.size()*k;
}
inline void solve(){
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
int t=0;
for(int i=0;i<x.size();++i){
tot+=abs(x[i]);
mp[i]=x[i];
q.push(make_pair(abs(x[i]),i));
}
while(!q.empty()){
int id=q.top().second,tmp=q.top().first;q.pop();
map<int,int>::iterator p=mp.lower_bound(id);
if(p==mp.end()||p->first!=id||abs(p->second)!=tmp)
continue;
while(t<a.size()&&abs(p->second)>a[t].first)
ans[a[t].second]=calc(a[t].first),++t;
if(p!=mp.begin())
if(p!=prev(mp.end())){
tmp=p->second,tot-=abs(p->second);
tmp+=prev(p)->second,tot-=abs(prev(p)->second);
tmp+=next(p)->second,tot-=abs(next(p)->second);
mp.erase(prev(p));
mp.erase(next(p));
p->second=tmp,tot+=abs(tmp);
q.push(make_pair(abs(tmp),id));
}
else{
tot-=abs(p->second);
mp.erase(p);
}
else if(p->second>0)
if(p!=prev(mp.end())){
tmp=p->second,tot-=abs(p->second);
tmp+=next(p)->second,tot-=abs(next(p)->second);
mp.erase(next(p));
if(tmp){
p->second=tmp,tot+=abs(tmp);
q.push(make_pair(abs(tmp),id));
}
else
mp.erase(p);
}
else{
tot-=abs(p->second);
mp.erase(p);
}
}
while(t<a.size())
ans[a[t].second]=calc(a[t].first),++t;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0,p,last=0;i<n;++i){
scanf("%d",&p);
if(p==last)
continue;
if(!x.empty()&&(x.back()<0&&p<last||x.back()>0&&p>last))
x.back()+=p-last;
else
x.push_back(p-last);
last=p;
}
for(int i=0,l;i<m;++i){
scanf("%d",&l);
a.push_back(make_pair(l,i));
}
sort(a.begin(),a.end());
solve();
for(int i=0;i<m;++i)
printf("%lld\n",ans[i]);
return 0;
}
所以 \(\frac{1}{4}\) 是有多喜欢STL啊

