P5017摆渡车

https://www.luogu.com.cn/problem/P5017

这个题用了很多奇怪的思想

也可能是我太孤陋寡闻了)

 

 

题解：

抽象化题目：

大概就是一段数轴，表示时间，令每个同学到来的时间为数轴上的一个点，

在某一时间安排车辆就相当于在某个点取一段左开右闭区间，每段长度>=m

等车时间等于该点距右方闭合处的距离

 

这个线性dp方程式就出来了

么的办法，不会编辑公式)

在递推 f_i  之前需要预处理仅在当前时间安排一辆车的损耗时间

即    

 

然后我们就想到了前缀和优化——降低时间复杂度

定义了sum[  ]  cnt[   ]两个数组，分别为前缀和、前缀点数目

 

 

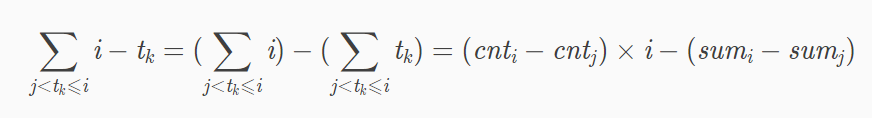
 于是改写一下dp

 

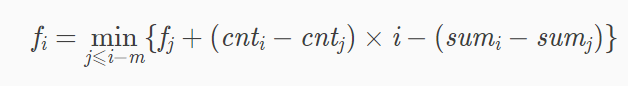
O  ( t²) 

 然后用这个粗糙的算法得到了50……

 

简单优化一下

原先 j ∈(  - ∞  , i -m )可以修改为( i - 2  *  m ,   i  -   m )

 

 O(mt)

因为如果间隔超过2m，就多出了一趟汽车往返的时间刚好满足减少等待时间

 

然后就混了个70

 

再优化一下下

可以见得假如在(  i  -  m ,  i  ]没有任何点

cnt[ i ] 与 cnt[  i - m  ]相当

那么直接将 f [ i ]  =  f [ i - m ]

然后我们就AC了 

时间复杂度优化为  O(nm² + t  )

 

#include<iostream>
#include<cstdio>

using namespace std;

int sum[4000005],cnt[4000005],f[4000005];

int main()
{
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    int n,m;
    cin>>n>>m;
    int x;
    int aux=1e7;
    int maxn=0;
    for(register int i=1;i<=n;i++)
    {
        cin>>x;maxn=max(maxn,x);
        cnt[x]++;sum[x]+=x;
    }
    for(register int i=1;i<maxn+m;i++)
        cnt[i]+=cnt[i-1],sum[i]+=sum[i-1];
        
    for(register int i=0;i<maxn+m;i++){
        if(i>=m && cnt[i-m] == cnt[i]) {f[i]=f[i-m];continue;}
        f[i] = cnt[i] * i - sum[i];
        for(register int j=(i-m-m+1>0)?i-m-m+1:0;j<=i-m;j++)
        {
//            if(i-m-m+1 < 0) j=0;
            f[i]=min(f[i],f[j] + ( cnt[i]-cnt[j]) * i - (sum[i] - sum[j]) );
        }
    }
    
    for(register int i=maxn;i<maxn+m;i++) aux=min(aux , f[i]);
    cout<<aux;
 } 

 

-end-