Self Adjusting RBQ
考虑一下 splay 的复杂度分析。
当需要递归的子树较大时,rotate 操作可以使势能降低。
反之势能会上升,但是次数不会超过 \(O(\log n)\)。
那么,当需要递归的子树较小的时候为什么不直接递归呢?
算法描述
当我们需要插入一个数字 \(x\),当前节点为 \(a\) 时,进行以下操作:
- 若子节点为空,直接结束。
- 若走一步之后为空,直接结束。
- 若可以向下走两步(还未找到插入位置)且两步之后的子树大小 < \(k\) 倍当前子树大小,则直接递归两步。
- 否则,若两步方向相同,则进行一次 zig 操作,否则进行 zig-zag 操作。
其中 \(k\) 为常数,zig 与 zig-zag 操作的定义与 splay 相同。
为了便于理解,代码贴在这里。
int insert(int a, int b)
{
if (!a)
return newnode(b);
while (true)
{
int x = (b >= tree[a].val), y = tree[a].son[x];
if (!y)
{
tree[a].son[x] = newnode(b);
break;
}
int c = (b >= tree[y].val);
if (tree[tree[y].son[c]].siz < tree[a].siz * eps)
{
tree[y].son[c] = insert(tree[y].son[c], b);
update(y); break;
}
if (c != x)
tree[a].son[x] = rotate(y, c);
a = rotate(a, x);
}
update(a);
return a;
}
后面我们将证明:每次旋转必定使势能降低 \(O(1)\),每次插入至多增加 \(O(1)\) 势能。
复杂度
我们定义势能 \(E = \sum \limits_{u} \log size(u)\)。
\(1, 2, 3\) 操作自不必多说,不影响势能,且至多进行 \(O(\log n)\) 次(每次使得当前子树大小缩小 \(k\) 倍)。
首先我们考虑 zig 操作的复杂度。
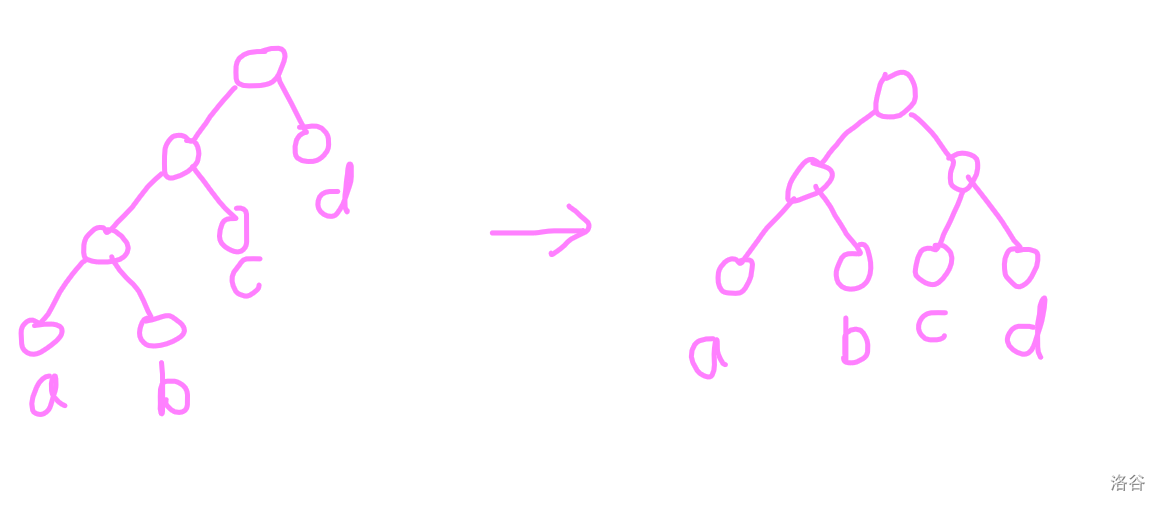
其中 \(k = \frac{a+b}{a+b+c+d}\)。
即证:\(\log(a+b+c) - \log(c+d) > 1\)。
我们只需要保证 \(a+b > 2(c+d)\) 即可。
因此 \(k > \frac{2}{3}\) 即可满足条件。
然后我们考虑 zig-zag 操作的复杂度。
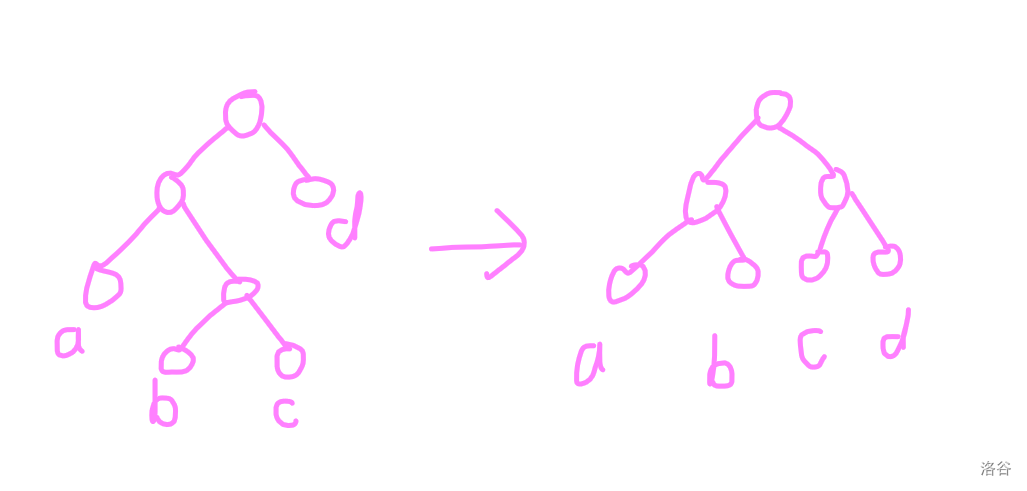
其中 \(k = \frac{b+c}{a+b+c+d}\)。
即证:\(\log(a+b+c)+\log(b+c)-\log(a+b)-\log(c+d) > 1\)。
这里 \(b\) 与 \(c\) 等价,因此我们钦定 \(b > c\)。
如果我们可以保证 \(\frac{1}{2}b^2 > 2ad\) 与 \(\frac{1}{2}b^2 > 2bd\) 均成立就可以了。
如果我们保证 \(b+c>8(a+d)\),由于 \(b>c\),所以 \(b>4(a+d)\),满足条件。
因此 \(k>\frac{8}{9}\) 时这部分成立。
因此只需要 \(b>2(a+d)\) 即可保证这部分成立,得到 \(k > \frac{4}{5}\)。
综上所述,取 \(k > \frac{8}{9}\) 可以保证 4 操作的复杂度。
(事实上我们可以将这个界降低到 \(\frac{\sqrt{13}+3}{\sqrt{13}+5} \approx 0.77\))
或许可以更低,但是毕竟是不影响复杂度的。
(Warning:实现时这个常数取的更低能换取更优秀的常数,但是可能会导致复杂度错误)
最后是插入导致的势能增加量。
考虑只有 \(1, 2, 3\) 操作导致当前深度增加,且插入后自下而上第 \(k\) 层的子树大小不小于 \(O(exp(k))\)。
那么势能增加量 \(\sum \limits _{k = 1} ^{\log n} \log (\exp(k)+1) - \log (
\exp(k)) \sim O(1)\)。
综上,递归操作单次不超过 \(O(\log n)\),旋转操作均摊 \(O(n)\)。
Bonus
由于势能函数定义与 splay 完全相同,所以可以继续使用 splay 的全部操作。
相较于常规的 splay,这种实现方式无法将需要访问的点旋转到根(只能保证旋转之后深度 \(O(\log n)\))。
但是换来了其它的性质(常数更小,理论不需要递归,不需要栈,不需要记录父节点,势能增加量更低)。
提交记录,用时 6.3s
由于前驱后继操作不方便实现,为了偷懒 使用了 \(kth(rank(x) - 1)\) 来实现。
平衡性
结束了吗?
如果只有上述操作,我们来看一看这个东西是否平衡。
若一个节点 \(u\) 的两个子节点 \(a, b\) 满足 \(\frac{1}{16} size(a) \le size(b) \le 16size(a)\),则称 \(u\) 为平衡的。
若 \(\frac{1}{17} size(a) < size(b) < \frac{1}{16} size(a)\) 或 \(a, b\) 互换,则称 \(u\) 是失衡的。
接下来我们要证明:任意时刻一条链上不会出现三个相邻的失衡点。
先考虑插入的过程。
考虑链上三个节点 \(a, b, c\),其中 \(a, c\) 的深度为偶数。
则我们有 \(size(c) < \frac{8}{9} size(a)\)。
若加点之后 \(a, b\) 均为失衡点,则有 \(size(c) > \frac{17^2}{18^2} size(a)\),显然不成立。
因此 \(a, b\) 中至少存在一个平衡点。
所以插入后的祖先链上不会出现三个相邻的失衡点。
然后考虑旋转的过程。
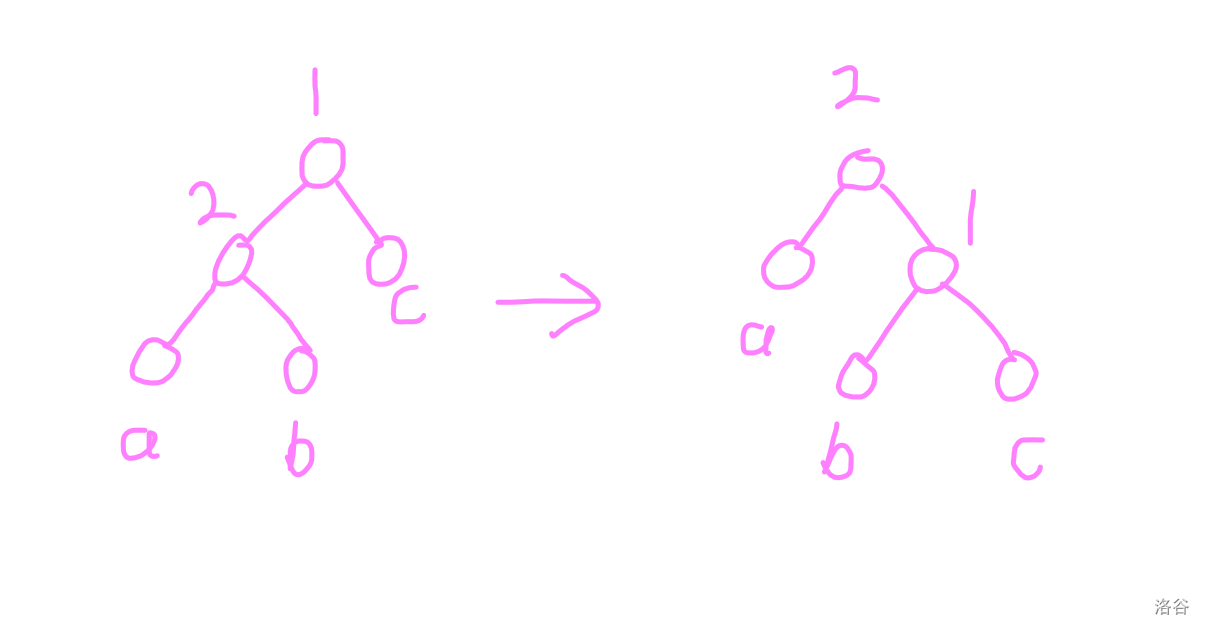
这里已知 \(a > 8(b+c)\)。
首先考虑 \(2\) 节点什么时候会失衡。
由于 \(a > b + c\),所以只能是 \(b+c < \frac{1}{16} a\)。
若旋转前 \(1, 2\) 中存在平衡点,则 \(b+c > \frac{1}{16} a\),不成立。
若旋转前 \(1, 2\) 均为失衡点,则 \(b > \frac{1}{17} a\),\(c > \frac{1}{17} (a + b)\)。
所以有 \(b+c > \frac{2}{17} a + \frac{1}{17^2} a > \frac{1}{16} a\)。
因此 \(2\) 节点旋转后必定平衡。
然后考虑 \(1\) 节点什么时候失衡。
由于 \(c > \frac{1}{17} (a+b) > \frac{1}{17}(9b + 8c) > \frac{9}{17}b\),所以只可能是 \(c > b\) 导致的失衡。
由于 \(c < \frac{1}{8} a\),\(b > \frac{1}{17} a\),所以有 \(b > \frac{8}{17} c\)。
综上,旋转之后 \(1, 2\) 一定都平衡。
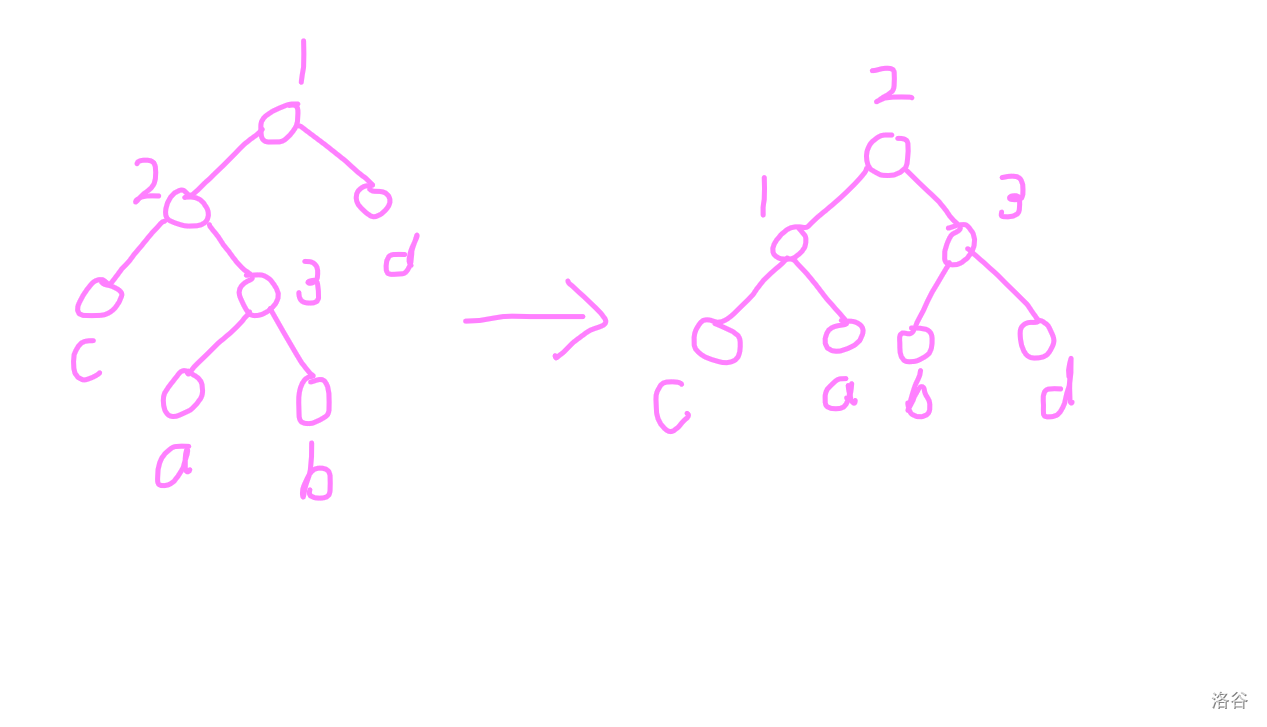
这里已知 \(a + b > 8(c + d)\)。
首先考虑 \(3\) 节点是否会失衡。
考虑旋转前 \(1, 2, 3\) 中至多出现两个失衡点,因此 \(d > \frac{18}{16 \times 17} b > \frac{1}{16} b\),\(3\) 节点不会失衡。
然后考虑 \(2\) 节点。
我们有 \(d > \frac{1}{18} (a+b+c+d)\),\(b > \frac{1}{18} (a+b) > \frac{8}{9 \times 18} (a+b+c+d)\)。
因此
我们又有 \(c > \frac{1}{17}(a+b)\),\(a > \frac{1}{18} (a+b)\)。
因此
综上,\(2\) 节点旋转后必定平衡。
最后是 \(1\) 节点。
若旋转前 \(2, 3\) 存在平衡节点,则 \(c > \frac{1}{16} a\),旋转后平衡。
若 \(2, 3\) 均失衡,则旋前 \(a, c\) 的父节点均失衡,旋后仍然失衡,不影响性质。
综上,进行旋转操作后仍能保持性质。
这样,我们就成功证明了这棵树重量平衡。
删除
Q:那么该如何删除节点呢?
这里我们使用经典做法:和右子树的后继节点交换然后删除后继。
首先,如果沿用势能分析的话,我们发现直接删即可。
毕竟势能是不增的。
但删除会导致失衡节点增加,影响我们的平衡性分析。
这可能会导致单次操作复杂度变高(因此查询也必须加入平衡维护)
因此我们需要在删除时加入维护平衡的操作。
大致来说,就是在递归过程中如果出现临近失衡的节点(删除后失衡),则反方向旋转。
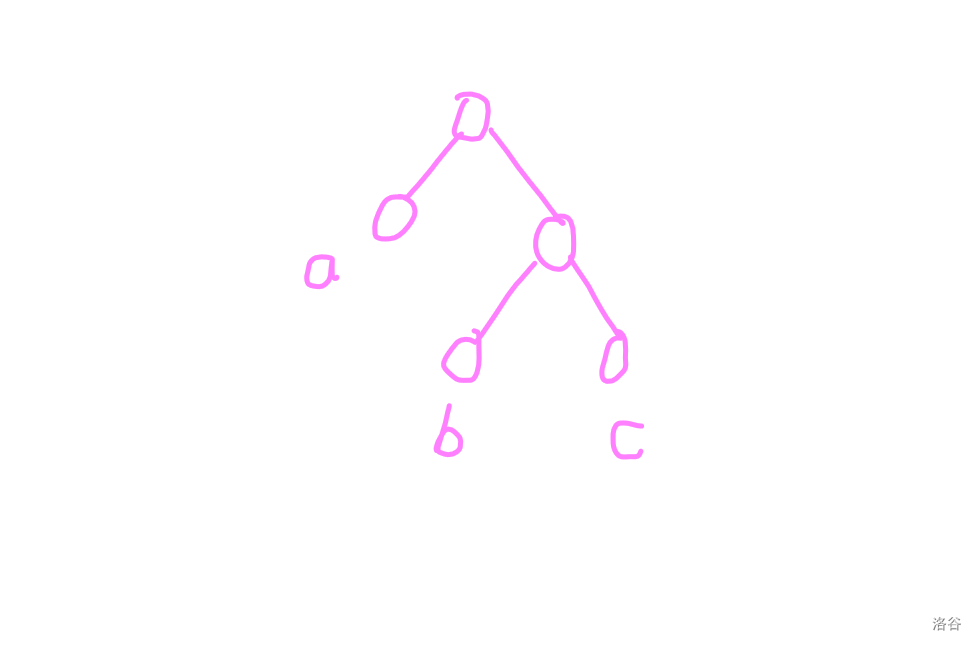
设我们要递归的节点为 \(a\),且 \(a < \frac{1}{16} (b+c)\)。
- 若 \(b > 7(a+c)\),则进行 zig-zag 操作。
- 否则进行一次 zig 操作。
(Warning:这里将 \(b > 7(a+c)\) 改为 \(b > 8(a+c)\) 会导致证不出来)
势能分析就免了。
我们直接证明其平衡即可。

这里我们有 \(b < \frac{7}{8}(a+b+c)\),\(c < \frac{1}{17}(a+b+c)\),因此 \(a > \frac{1}{16} (a+b+c)\),先保证 \(2\) 节点性质不被破坏。
我们还有 \(b > \frac{1}{17} a\),\(c > \frac{1}{17} a\),所以 \(b+c > \frac{1}{9} a\),即可保证 \(2\) 节点不临近失衡。

熟悉吗?
首先我们有 \(b+d > (\frac{1}{18} + \frac{7}{8 \times 18})(a+b+c+d) > \frac{1}{10}(a+c)\),则 \(2\) 节点不会临近失衡。
剩余的的平衡性分析可以直接沿用前面的,因为并不需要 \(a + b > 8(c + d)\) 这个条件。
综上,旋转操作可以使当前节点摆脱临近失衡状态且不影响整棵树的平衡性质。
结算
既然如此,就只需要在插入、删除的时候进行旋转操作。
由于任意时刻平衡,所以查询时直接遍历即可,不需要进行平衡维护。
洛谷板子(\(10^6\)):
提交记录,5.7s
5.48s,去掉了 update 并优化了逻辑
Loj 板子(\(10^5\)):
ofast 加持 53ms



 浙公网安备 33010602011771号
浙公网安备 33010602011771号