判断点是否在多边形内 （附C实现代码）

如何判断一个点是否在多边形内部？

（1）面积和判别法：判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形，相等则在多边形内部。

（2）夹角和判别法：判断目标点与所有边的夹角和是否为360度，为360度则在多边形内部。

（3）引射线法：从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

本文采用引射线法。

原理：从测试点引一条垂直于y轴的射线，若射线与多边形交点为奇数时，则测试点在多边形内，若为偶数点，则在多边形外。测试点在多边形的边上时则需特殊考虑。

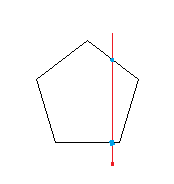
如图所示 交点为2点，点在图形外。

算法图解：

 

参考代码：

/************************************************************
** 函数名称:  InOrOutPolygon
** 功能描述:  判断点在多边形内外
** 输入参数:  nvert 顶点个数 vertx 多边形顶点x坐标数组 verty 多边形顶点y坐标数组 
              testx 被判断点位置x坐标 testy 被判断点位置y坐标
** 输出参数:  NULL
** 返 回 值:  0:外 1:内
** 作    者:  
** 日    期:  2018年3月21日
**************************************************************/
int InOrOutPolygon(int nvert, float *vertx, float *verty, float testx, float testy)
{
  int i, j, crossings = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) 
  {
      // 点在两个x之间 且以点垂直y轴向上做射线
    if(((vertx[i]>testx) != (vertx[j]>testx)) 
    && (testx > (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]))
       crossings++;
  }
  return (crossings % 2 != 0);
}

代码原理：

　　        引射线法是做一条射线，判断与多边形每条边的交点。

               那么我们即可认为做一条方向向上且与y轴垂直的射线。

               所以只要测试点在边的下方且横坐标在边两顶点之间，即有一个交点，否则无交点。

               那么我们只需要通过2点（(x1,y1)(x2,y2)）求出边的直线方程，将测试点（x,y）带入边的直线方程，测试点满足 x1<x<x2 或 x2<x<x1 且y<k(x-x1)+y1

               若点在边界则测试点满足 x1<x<x2 或 x2<x<x1 且y=k(x-x1)+y1

 参考资料：http://www.cnblogs.com/luxiaoxun/p/3722358.html

 

2018.3.30 更新

以上方法针对普通情况可适用，但是针对某些特殊情况，可能出现判断错误的情况

1.若射线引出的点直接穿过顶点。若按上述算法进行计算，则穿过点的数量为0 得出点在多边形外。

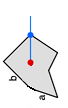
所以我们计算时，应当取半开半闭区间，即将顶点算入线中，但是每条线只计算其一边的顶点（若为闭区间，则会重复计算顶点）

2.若射线穿过定点

 

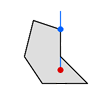
使用1所述方法可以解决。

参考代码：

int InOrOutPolygon(int nvert, float *vertx, float *verty, float testx, float testy)
{
//  int i, j, crossings = 0;
    crossings = 0;
    for (i = 0, j = nvert-1; i < nvert; j = i++) 
    {
    // 点在两个x之间 且以点垂直y轴向上做射线
    x1[i] = vertx[i];
    x1[j] = vertx[j];
    y1[i] = verty[i];
    y1[j] = verty[j];
    if((((vertx[i] < testx) && (vertx[j] >= testx))||((vertx[i] >= testx) && (vertx[j] < testx)))     
    &&   (testx > (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]))
       crossings++;
    }
    return (crossings % 2 != 0);
}

关于这个算法的具体的更多图形例子：http://alienryderflex.com/polygon/